|
|
Описание лабораторной установкиБукерма л. б. ФИЗИКА ЧАСТЬ 3. КОЛЕБАНИЯ
Методические указания по выполнению лабораторных работ по физике
для студентов, обучающихся по специальности 190601 «Автомобили и автомобильное хозяйство»
Бронницы 2011
Бронницкий филиал «МОСКОВСКИЙ АВТОМОБИЛЬНО-ДОРОЖНЫЙ
Кафедра МЕН
Букерма л. б. ФИЗИКА ЧАСТЬ 3. КОЛЕБАНИЯ
Методические указания по выполнению лабораторных работ по физике
для студентов, обучающихся по специальности 190601 «Автомобили и автомобильное хозяйство»
Бронницы 2011 Введение Колебательные законы описывают большой круг явлений окружающей нас действительности. Различают механические и электромагнитные колебания, свободные и вынужденные, гармонические и затухающие. Для описания вибраций автомобиля используют модель вынужденных затухающих колебаний. Лабораторные работы по данной теме призваны описать все виды колебательного движения. В ходе проведения лабораторных работ определяются основные параметры колебательной системы – частота, период колебаний, добротность системы, логарифмический декремент затухания, время релаксации. Часть работ проводится с использованием компьютерных моделей, позволяющих одновременно снимать показания и строить графики зависимости колеблющихся величин от времени и амплитудно-частотной характеристики.
Перечень лабораторных работ 1. Изучение собственных колебаний механических систем. 2. Измерение ускорения свободного падения с помощью математического и физического маятников. 3. Свободные колебания в RLC-контуре 4. Вынужденные колебания
Лабораторная работа №1 ИЗУЧЕНИЕ СОБСТВЕННЫХ КОЛЕБАНИЙ МЕХАНИЧЕСКИХ СИСТЕМ
Цель работы: – ознакомиться с основными закономерностями свободных колебаний, экспериментальная проверка зависимости собственной частоты колебаний w0 от физических параметров системы: массы маятника m и коэффициента упругости пружины k, изучение влияния сопротивления среды (сил вязкого трения и лобового сопротивления) на процесс колебаний
Оборудование: · штатив со шкалой · источник питания · миллиамперметр · вольтметр Основные понятия Дифференциальное уравнение, описывающее динамику одномерных затухающих упругих колебаний при наличии сил сопротивления, пропорциональных скорости, можно записать на основе законов Ньютона, Гука и Стокса в виде
а его решение – в виде X(t)=X0(t)cos(ωt+ α) (2)
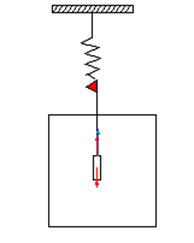
Здесь X(t) - мгновенное значение смещения маятника от положения равновесия, которое определяется условием равенства нулю геометрической суммы всех сил, действующих на маятник в статическом (неподвижном) положении. В общем случае это сила тяжести, упругости и архимедова выталкивающая сила (рисунок 1);
Рисунок 1 Пружинный маятник
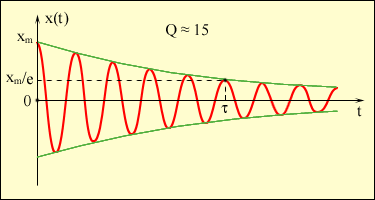
X0(t)=A·e-δt амплитуда затухающих колебаний, монотонно убывающая по закону экспоненты от начального значения A (рис. 2); α- начальная фаза колебаний, определяемая способом возбуждения колебаний маятника; ω0 - частота собственных колебаний маятника; δ-коэффициент затухания; r-коэффициент сопротивления; k-коэффициент упругости пружины; m-масса груза, значительно большая, чем масса пружины.
Рисунок 2 Затухающие колебания
Пунктирная кривая
ω²=ω0²-δ²; δ=r/2m; ω0²=k/m (3)
При отсутствии сил трений (точнее при их пренебрежимой малости, например, при колебаниях в воздухе величина r=0 и, следовательно, δ=0 A=Xm; ω=ω0; T0=2π/ω0 причем α и A определяются лишь начальными условиями, а ω0- внутренними свойствами системы. При учете сил вязкого трения основной величиной, характеризующей затухание, является логарифмический декремент затухания θ , определяемый как натуральный логарифм отношения амплитуд колебаний, отстоящих по времени на один период колебаний T .
На практике для измерения логарифмического декремента формула непригодна, т.к. за одни период колебаний изменяется очень незначительно. Обычно измеряют, разделенные достаточно большим промежутком времени nT , где n - число колебаний между изменениями амплитуд. В этом случае
Для измерения логарифмического декремента затухания колебаний пользуются формулой (5). Физический смысл величины θ состоит в том, что с ее помощью можно определить полное число колебаний системы за время ее релаксации τ , т.е. за то время, за которое амплитуда уменьшается в e ≈ 2,7 раз. A(t+τ)=A(t)/e; Ne=τ/T; τ=1/θ; Ne =1/θ
В данной лабораторной работе нужно выполнить три задания: 1) измерить собственную частоту колебаний маятника статическим методом; 2) измерить собственную частоту колебаний маятника динамическим методом; 3) измерить логарифмический декремент затухания колебаний. При этом можно ограничиться одной пружиной и одним грузом.
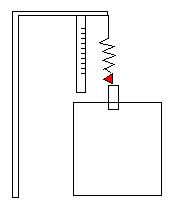
Описание лабораторной установки 1. Общий вид лабораторной установки изображен на рисунке 3. Опыт может проводиться с помощью сменного набора пружин и грузов, подведенных на штативе . Растяжение пружины определяется по измерительной шкале с помощью указателя . При изучении затухающих колебаний используется также сосуд с водой . Измерение времени проводится с помощью секундомера. Набор грузов может содержать грузы различной форме и массы; последняя указывается на грузах.
Рисунок 3 Схема лабораторной установки 2. При выполнении лабораторной работы студент должен соблюдать правила по технике безопасности, а также следить за тем, чтобы металлический груз, подвешенный на пружине, не падал на дно стеклянного сосуда или не соударялся с его стенками, т.к. в этом случае сосуд легко может быть разбит. Для сохранности стеклянного сосуда на его дно кладется резиновая прокладка. От студента требуется бережное отношение к оборудованию.

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 (1)
(1)
 характеризует закон убывания амплитуды.
характеризует закон убывания амплитуды.
 ;
;  (4)
(4)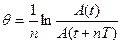 (5)
(5)