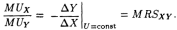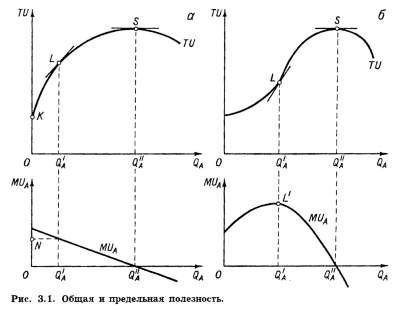
|
|
Предпочтения потребителя и его потребительский выбор. Кривые безразличия и норма замены.Количественный подход к анализу полезности основан на представлении о возможности измерения различных благ в гипотетических единицах полезности ≈ ютилах (от англ. utility ≈ полезность). В частности, предполагается: потребитель может сказать, что ежедневное потребление им 1 яблока приносит ему удовлетворение, скажем, в 20 ютилов, ежедневное потребление 2 яблок ≈ 38 ютилов, ежедневное потребление 2 яблок и 1 сигареты ≈ 50 ютилов, ежедневное потребление 2 яблок, 1 сигареты и 1 апельсина ≈ 63 ютила и т.д. Следует подчеркнуть, что количественные оценки полезности того или иного товара или товарного набора имеют исключительно индивидуальный, субъективный характер. Количественный подход не предполагает возможности объективного измерения полезности того или иного товара в ютилах. Один и тот же продукт может представлять большую ценность для одного потребителя и никакой ценности ≈ для другого. В приведенном выше примере речь идет, видимо, о заядлом курильщике, поскольку добавление к 2 яблокам 1 сигареты существенно увеличило полезность товарного набора. Количественный подход обычно не предусматривает также возможности соизмерения объемов удовлетворения, получаемых различными потребителями. Экономисты неоднократно пытались избавиться от термина "полезность", имеющего некоторый оценочный характер, найти ему подходящую замену. Так, известный русский экономист Н. X. Бунге предлагал использовать термин "годность" (Nutze ≈ нем.). "Потребность в наркотических веществах, ≈ писал он, ≈ несомненна, но можно ли сказать, что опиум и гашиш полезны для курильщиков, ≈ они только годны как вещество для опьянения".1 Итало-швейцарский экономист и социолог В. Парето предлагал заменить термин "полезность" неологизмом ophelimite, образованным им от греческого iojelimoz, означавшим соответствие между вещью и желанием. Французский экономист Ш. Жид предлагал использовать термин "желаемость" (desirabilite ≈ фр.), считая, что он "не предполагает у желания нравственных или безнравственных черт, разумных или безрассудных".2 В поддержку термина "желаемость" высказывался и известный американский экономист и статистик И. Фишер. "Полезность, ≈ считал он, ≈ является наследием Бентама и его теории удовольствия и страдания".3 Фишер указывал и на предпочтительность антонима "нежелательность" по сравнению с "бесполезностью". (Совсем неудачен употребляемый в нашей современной литературе антоним "антиполезность"). Тем не менее термин "полезность" пережил своих критиков и используется поныне. Итак, в количественной теории полезности предполагается, что потребитель может дать количественную оценку в ютилах полезности любого потребляемого им товарного набора. Формально это можно записать в виде функции общей полезности: TU = F(QA, QB, ..., QZ), (3.1) где TU ≈ общая полезность данного товарного набора; QA, QB, ┘, QZ ≈ объемы потребления товаров А, В, ..., Z в единицу времени. Большое значение имеют предположения о характере функции общей полезности. Зафиксируем объемы потребления товаров B,C,...,Z. Рассмотрим, как изменяется общая полезность товарного набора в зависимости от объема потребления товара А (например, яблок). В верхней части рис. 3.1,a изображена эта зависимость. Длина отрезка ОК равна полезности товарного набора при фиксированных нами объемах товаров В, С,..., Z и при нулевом объеме потребления товара А. В количественной теории предполагается, что функцияTU в верхней части рис. 3.1,а возрастающая (чем больше яблок, тем большую полезность имеет товарный набор) и выпуклая вверх (каждое последующее яблоко увеличивает общую полезность товарного набора на меньшую величину, чем предыдущее). В принципе эта функция может иметь точку максимума (S), после которой она становится убывающей (представьте, что Вас ежемесячно заставляют потреблять по 100 кг яблок).
В нижней части рис. 3.1,а изображена зависимость предельной полезности яблок от объема их потребления. Предельная полезность ≈ это прирост общей полезности товарного набора при увеличении объема потребления данного товара на одну единицу. Математически предельная полезность товара есть частная производная общей полезности товарного набора (3.1) по объему потребления г-того товара:
Геометрически значение предельной полезности (длина отрезка ON) равно тангенсу угла наклона касательной к кривой TU в точке L. Поскольку линия TU выпукла вверх, с увеличением объема потребления г-того товара угол наклона этой касательной уменьшается и, следовательно, понижается и предельная полезность товара. Если при некотором объеме его потребления (на нашем рисунке Q▓'A) функция общей полезности достигает максимума, то одновременно предельная полезность товара становится нулевой. Принцип убывающей предельной полезности часто называют первым законом Госсена, по имени немецкого экономиста Г. Госсена (1810-1859), впервые сформулировавшего его в 1854 г.4 Этот закон содержит два положения. Первое констатирует убывание полезности последующих единиц блага в одном непрерывном акте потребления, так что в пределе достигается полное насыщение этим благом. Второе констатирует убывание полезности первых единиц блага при повторных актах потребления. Принцип убывающей предельной полезности по существу аналогичен так называемому основному психофизическому закону Вебера-Фехнера,5 характеризующему связь между силой раздражителя (стимула) и интенсивностью ощущения. Согласно этому закону, раздражения равной интенсивности, повторяющиеся в течение определенного времени, сопровождаются снижением интенсивности ощущений. Принцип убывающей предельной полезности заключается в том, что с ростом потребления какого-то одного блага (при неизменном объеме потребления всех остальных) общая полезность, получаемая потребителем, возрастает, но возрастает все более медленно. Математически это означает, что первая производная функции общей полезности по количеству данного блага положительна, а вторая ≈ отрицательна:
Однако принцип убывающей предельной полезности отнюдь не универсален. Во многих случаях предельная полезность последующих единиц блага сначала увеличивается, достигает максимума и лишь затем начинает снижаться. Такая зависимость характерна для небольших порций делимых благ. Вторая затяжка выкуриваемой утром сигареты, возможно, имеет для любителя большую полезность, чем первая, а третья большую, чем вторая. Такая ситуация показана на рис. 3.1,6. В интервале от нуля до Q'A общая полезность возрастает быстрее, чем увеличивается объем потребления блага, растет и предельная полезность. В интервале от Q'A до Q▓'A общая полезность растет медленнее, чем объем потребления, а предельная снижается от максимального уровня (в точке L') до нуля. Математически это означает, что на участке от нуля до Q'A и первая, и вторая частные производные функции общей полезности по объему потребления данного блага положительны:
Таким образом, принцип убывающей предельной полезности, или первый закон Госсена, справедлив лишь в том случае, если вторая частная производная функции общей полезности отрицательна. Однако поскольку потребитель покупает на рынке не отдельные акты потребления (в нашем примере ≈затяжки), а определенные блага (в нашем примере ≈ сигареты), мы можем считать, что для обращающихся на рынке товаров первый закон Госсена (3.3) выполняется. Предположим теперь, что потребитель располагает некоторым доходом; цены на товары A, B, ..., Z не зависят от его поведения и равны соответственно PA, PB, ┘,PZ товарного дефицита нет; все товары являются бесконечно делимыми (как, например, колбаса, сливочное масло и т.д.). При этих предположениях потребитель достигнет максимума удовлетворения, если он распределит свои средства на покупку различных товаров таким образом, что: 1) для всех реально покупаемых им товаров А, В, С,... имеет место
где MUA, MUB, MUC ≈ предельные полезности товаров А, В, С; l ≈ некоторая величина, характеризующая предельную полезность денег;6 2) для всех непокупаемых им товаров Y, Z,... имеет место
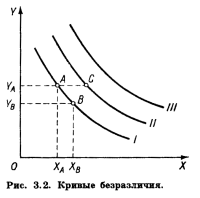
Докажем первую часть утверждения. Предположим обратное: товары А и В реально покупаются потребителем, но MUA/PA > MUB/PB. Для определенности предположим, что МUA = 40 ютилов в расчете на килограмм, PA = 2 руб. за килограмм, МUB = 20 ютилов в расчете на килограмм, PB = 4 руб. за килограмм. В результате (МUA/PA = 40 ютилов/2 рубля) > (20 ютилов/4 рубля = МUB/PB Очевидно, что покупатель при этом не достигает максимума удовлетворения. Он может сократить потребление товара В на 1 кг, при этом он потеряет 20 ютилов. Но за счет сэкономленных 4 руб. он может купить дополнительно 2 кг товара А и получить дополнительно примерно 80 ютилов. (Слово "примерно" здесь использовано потому, что 2-й дополнительный килограмм товара А может принести меньшую полезность, чем 1-й, скажем, только 39 ютилов, а не 40). Чистый выигрыш составит примерно 80 - 20 = 60 ютилов. С уменьшением потребления товара В его предельная полезность уменьшается. Поэтому разница между МUA/PA и МUB/PBбудет сокращаться. Перераспределение расходов будет происходить до тех пор, пока отношение предельной полезности к цене для каждого реально покупаемого товара не станет одинаковым. Равенство (3.4) можно интерпретировать следующим образом. Отношение МUA/PAпредставляет собой прирост общей полезности в результате увеличения расходов потребителя на товар A на 1 руб. Очевидно, что в состоянии оптимума потребителя все подобные отношения для реально покупаемых товаров должны быть равны друг другу. И любое из них может рассматриваться как предельная полезность денег (точнее, 1 руб.). Величина А показывает, на сколько ютилов увеличивается общая полезность при увеличении дохода потребителя на 1 руб. Вторую часть утверждения можно доказать совершенно аналогичным образом, от противного. Смысл формулы (3.5) заключается в том, что если уже 1-й рубль, израсходованный на покупку товара Z, приносит потребителю недостаточно высокую полезность, то он вообще отказывается от потребления этого товара. Таким образом, равенство (3.4) показывает, что в оптимуме (максимум полезности при данных вкусах потребителя, ценах и доходах) полезность, извлекаемая из последней денежной единицы, потраченной на покупку какого-либо товара, одинакова, независимо от того, на какой именно товар она израсходована. Это положение получило название второго закона Госсена. Конечно, потребитель может раскаяться в покупке, даже удовлетворяющей равенству (3.4). Это будет означать, что "за время от покупки до раскаяния в ней" знак в (3.4) для данного товара изменился на противоположный.7 Попытаемся показать теперь на основе количественного подхода, что объем спроса и цена связаны обратной зависимостью. Снова рассмотрим равенство (3.4). Допустим, что цена на покупаемый потребителем товар А повысилась. В результате первое отношение в равенстве (3.4) уменьшилось. Чтобы восстановить равенство (3.4) и максимизировать общую полезность, потребитель начнет сокращать потребление товара А. Аналогичным образом будут поступать и другие потребители. Таким образом, с повышением цены товара объем спроса на него сокращается Кривая безразличия ≈ это множество точек, каждая из которых представляет собой такой набор из двух товаров, что потребителю безразлично, какой из этих наборов выбрать. Если заполнить двухмерную плоскость кривыми безразличия так плотно, как это возможно, получим карту безразличия. На рис. 3.2 товарный набор А включает ХА единиц товара X и YА единиц товара Y, товарный набор В включает ХB единиц товара X и YB единиц товара Y. Если с точки зрения данного потребителя наборы А и В равноценны, то точки А и В лежат на одной и той же кривой безразличия.
Кривые безразличия обладают следующими свойствами. А. Кривая безразличия, лежащая выше и правее другой кривой, представляет собой более предпочтительные для данного потребителя наборы товаров. Рассмотрим на рис. 3.2 кривые безразличия I и II. Набор С содержит такое же количество товара Y, что и набор А. Но набор С включает в себя большее количество товара X. Из аксиомы о ненасыщении следует, что С > А. Все наборы, лежащие на кривой безразличия I, с точки зрения нашего потребителя равноценны. То же относится и ко всем наборам, лежащим на кривой II. Из аксиомы о транзитивности следует, что любой набор, лежащий на кривой II, для нашего потребителя предпочтительнее любого набора, лежащего на кривой I. Б. Кривые безразличия имеют отрицательный наклон. Пусть дана некоторая точка А (рис. 3.3), характеризующая определенную комбинацию товаров. Проведем через нее две взаимно перпендикулярные прямые. Очевидно, что все точки, лежащие в III квадранте, соответствуют большим, а все точки, лежащие в I квадранте, ≈ меньшим количествам товаров X и Y, чем точкаА. В соответствии с аксиомой ненасыщения точки, лежащие в III квадранте, более предпочтительны, а лежащие в I квадранте ≈ менее предпочтительны, чем А. Следовательно, точки, безразличные А, например С, или В, или D, или G, должны находиться либо во II, либо в IV квадранте. И значит, кривая безразличия должна иметь отрицательный наклон.
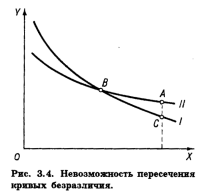
В. Кривые безразличия никогда не пересекаются. Предположим противное. Пусть кривые безразличия I и II на рис. 3.4 пересеклись в точке В. Из аксиомы о ненасыщении следует, что А > С. Наборы В и С лежат на одной кривой безразличия I. Поэтому В ~ С. Наборы А и В лежат на одной кривой безразличия II. Поэтому А ~ В. Из аксиомы о транзитивности следует, что А ~ С. Однако не могут одновременно быть А > С и А ~ С. Следовательно, кривые безразличия не могут пересекаться.
Заметим, что в отличие от непересекающихся прямых, которые должны быть параллельными, кривые могут не пересекаться и не будучи параллельными. Г. Кривая безразличия может быть проведена через любую точку пространства товаров. Говорят еще, что кривая безразличия не имеет "толщины". Это свойство любых линий в Евклидовой геометрии, оно является безусловно определенной идеализацией, абстракцией реального мира. Чтобы сделать его более реалистичным, необходимо при выборе единицы измерения товаров учитывать порог восприятия. Д. Кривые безразличия выпуклы к началу координат. Это свойство в отличие от ранее перечисленных не может быть выведено непосредственно из аксиом рационального поведения. Оно просто отражает принцип диверсификации потребления. Позднее мы вернемся к этому свойству кривых безразличия. Основным рабочим понятием порядковой теории полезности является предельная норма замещения (MRS; marginal rate of substitution ≈ англ.). Предельной нормой замещения благом X блага Y(MRSXY) называют количество блага Y, которое должно быть сокращено "в обмен" на увеличение количества блага X на единицу, с тем чтобы уровень удовлетворения потребителя остался неизменным:
Поскольку отношение DY/DX по определению отрицательно, минус, вводимый перед правой частью, делает значение нормы замещения положительным.
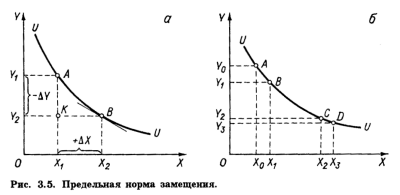
Пусть потребитель безразличен между наборами А и В (рис. 3.5, а). Значит, норма, по которой он согласен замещать благо Y благом X, оставаясь при этом на одной и той же кривой безразличия, составит (OY1 - OY2)/(OY1 - OY2) = - DY/DX = -AK/KB По мере приближения точки А к точке В отношение АК/КВ будет приближаться к наклону касательной в точке В. В пределе в окрестностях В наклон кривой (или касательной) в этой точке и есть предельная норма замещения:
Предельная норма замещения может принимать различные значения, она может быть равна нулю, может быть неизменной или меняться при движении вдоль кривой безразличия. В случае выпуклости к началу координат, как на рис. 3.5, MRS убывает по мере замещения одного блага другим, т.е. потребитель соглашается отдавать все меньшее количество замещаемого блага за одно и то же количество замещающего (аналог убывающей предельной полезности). Так, на рис. 3.5,б потребитель, находясь в точке А, готов уступить Y0Y1 блага Y взамен приращения блага X на X0X1. Однако, располагая набором С, он за равновеликое приращение блага X(X2X3 = X0X1) согласится уступить лишь Y2Y3 блага Y, что меньше Y0Y1
Возможно, далее, что товары вообще не могут заменять друг друга, как например правый и левый ботинок. Потребитель получит одно и то же удовлетворение, имея один левый и два правых ботинка, как и имея, наоборот, два левых и один правый. Такие товары жестко дополняют друг друга. В этом случае каждая кривая безразличия вырождается в два взаимно перпендикулярных отрезка (U2U2 на рис. 3.6). Наконец, иногда возможно, что, чем больше какого-то товара имеет потребитель, тем больше он хотел бы иметь его. В этом случае кривая безразличия вогнута к началу координат и норма замещения возрастает (U3U3 на рис. 3.6). Хотя ни один из этих вариантов не может быть исключен, выпуклость кривых безразличия и убывающая норма замещения представляют наиболее общую и распространенную ситуацию. Почему?
Лишь I квадрант интересовал создателей теории и лишь в I квадранте существует проблема выбора и ее оптимальное решение. Количественная и порядковая теории полезности ≈ это теории, построенные на основе различных предположений о поведении потребителей. Тем не менее в этих теориях можно обнаружить много общего. В частности, кривые безразличия в порядковой теории можно рассматривать как линии уровня функции общей полезности TU = F(X,Y) в количественной теории. Предположение об уменьшающейся предельной норме замещения в порядковой теории имеет тот же смысл, что и предположение о понижающейся предельной полезности в количественной теории. Только во втором случае полезность товаров оценивается в ютилах. В первом же случае полезность каждой дополнительной единицы товара оценивается объемом другого товара, которым потребитель согласен пожертвовать. Кроме того, можно показать, что MUX/MUY = MRSXY (3.8) Увеличим количество товара X в наборе на очень незначительную величину DX. В результате общая полезность набора увеличится на MUXDX. Определим теперь, на сколько единиц необходимо сократить количество товара Y, чтобы общая полезность товарного набора не изменилась. Для этого MUXDX нужно разделить на MUY: DY = MUXDX/MUY Знак минус необходим, поскольку X и Y меняются в противоположных направлениях. Последнее равенство можно преобразовать к виду MUX/MUY = -DY/DX (3.9) Напомним, что DX и DY выбраны такими, что общая полезность набора остается неизменной. Следовательно,
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|
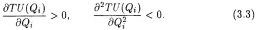
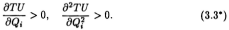
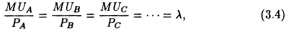
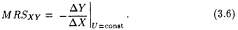
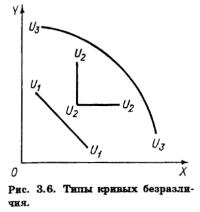Для двух совершенно взаимозаменяемых товаров MRS = const. В этом случае кривые безразличия вырождаются в прямые линии (линия U1U1 на рис. 3.6). Обычно такие товары рассматриваются как один товар.
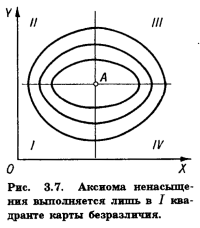Порядковая теория полезности концентрирует внимание на I квадранте карты безразличия, представленной на рис. 3.7. В этом квадранте аксиома ненасыщения выполняется для обоих благ ≈ X и Y, тогда как в III квадранте потребности индивидуума в обоих благах насыщены и увеличение их потребления приведет лишь к перенасыщению. В квадранте II избыточным был бы рост потребления блага Y, в квадранте IV ≈ блага X.