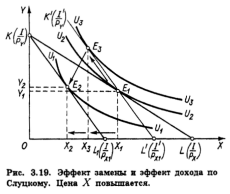
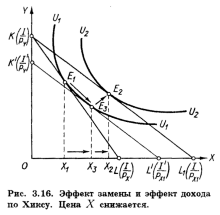
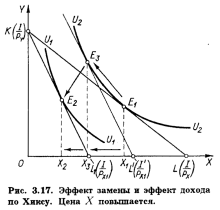
Эффект замены и эффект дохода по слуцкому

Подход Слуцкого к разложению общего результата изменения цены на эффект дохода и эффект замены отличается от подхода Хикса трактовкой реального дохода. Элиминирование эффекта дохода достигается определением такого его уровня, который обеспечил бы потребителю возможность приобрести после изменения цен тот же самый набор товаров, что и до изменения, а не сохранить прежний уровень удовлетворения, как это предполагается в модели Хикса.

Поэтому на рис. 3.19 вспомогательная бюджетная прямая K'L', параллельная KL₁, проводится не как касательная к прежней кривой безразличия U₂U₂, а строго через точку E₁, соответствующую оптимальному набору товаров X и Y при прежнем соотношении цен. Очевидно, она окажется касательной к более высокой, чем U₂U₂ кривой безразличия U₃U₃, что означает и возможность достигнуть (в случае полной компенсации потребителю падения его покупательной способности) более высокого уровня удовлетворения, чем при использовании модели Хикса. Таким образом, общий результат повышения цены товара X (Х₁ - Х₂) разлагается на эффект замены (Х₁ ≈ Х₃) и эффект дохода (Х₃ - Х₂). Заметим, что движение отE₁ к E₂ происходит не вдоль кривой безразличия, как на рис. 3.16 и 3.17, а вдоль вспомогательной бюджетной прямой K'L'

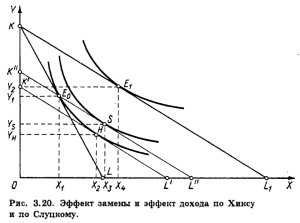
Сравнив два подхода, мы видим, что метод Хикса предполагает знание потребительских предпочтений, кривых безразличия, тогда как метод Слуцкого не требует этого, он базируется на наблюдаемых и регистрируемых фактах поведения потребителя на рынке.

ОБОБЩЕНИЕ

Различия в подходах Хикса и Слуцкого удобно рассмотреть, совместив их на одном рисунке (рис. 3.20).

Здесь KL ≈ бюджетная прямая при номинальном доходе I и ценах Р_X и Р_Y, ее уравнение

XР_X+ YР_Y=I;

KL₁ ≈ бюджетная прямая при том же номинальном доходе I и ценах Р_X + DР_X и Р_Y (причем DР_X- < 0), ее уравнение

X(Р_X + DР_X) + YР_Y = I;

E₀ и E₁ - комбинации товаров X и Y до и соответственно после снижения цены X; K▓L▓ иK▓▓L▓▓ - вспомогательные соответственно по Хиксу и по Слуцкому. Их уравнения

I_H = X(Р_X + DР_X) + YР_Y|_{U = const}

I_S = X(Р_X + DР_X) + YР_Y|_{X, Y = const}

H и S- комбинации товаров X и Y, отвечающие требованию неизменного реального дохода соответственно по Хиксу и по Слуцкому.

Теперь мы можем представить методы разложения общего результата изменения цены Р_X по Хиксу и по Слуцкому в виде двух равенств:

(Х₄ - Х₁) = (Х₄ - Х₂) + (Х₂ - Х₁) (по Хиксу), (3.14)

(Х₄ - Х₁) = (Х₄ - Х₂) + (Х₂ - Х₁) (по Слуцкому). (3.15)

Левые части (3.14) и (3.15) характеризуют общий результат изменения цены Р_X в мере изменения объема спроса на товар X, и в обоих случаях они одинаковы. Правые части представляют суммы эффектов дохода и замены. Очевидно, что разница в распределении общего результата на эффект дохода и эффект замены составляет Х₃≈Х₂- В (3.14) эта величина входит в эффект дохода, в (3.15) ≈ в эффект замены.

Можно показать, что величина Х₃-Х₂ ╝ 0 при DР_X╝ 0, так что при малых изменениях Р_Xподходы Хикса и Слуцкого дают практически одинаковый результат.²

В дифференциальной форме равенства (3.14) и (3.15) имеют вид

(по Хиксу)

(по Слуцкому)

Левые части (3.16) и (3.17) одинаковы и представляют общий результат изменения Р_X при неизменных номинальном доходе I и цене Р_Y. Здесь dX/dР_X можно интерпретировать как наклон линии спроса на товар X, если Р_X принять как аргумент, а объем спроса ≈ как функцию.

Правые части представляют, как и в (3.14) и (3.15), суммы эффектов дохода и замены. При этом в (3.17) Х₁ = dI/dР_X, поскольку при изменении Р_X на DР_X для приобретения прежнего товарного набора E₀ (Х₁, Y₁) потребовалось бы компенсирующее изменение номинального дохода потребителя на Х₁DР_X, или в расчете на единицу изменения цены Х₁DР_X/DР_X, т.е. Х₁.

Эффект замены dХ/dР_X всегда отрицателен, так как цена и количество изменяются в противоположных направлениях.

Знак перед первым слагаемым правой части (эффект дохода) зависит от знака сомножителяdХ/dI. Если /iX ≈ нормальный товар, dХ/dI > 0 и эффект дохода отрицателен (снижение цены увеличивает реальный доход, и покупки нормального товара возрастают). Если X ≈некачественный товар, dХ/dI < 0 и эффект дохода положителен (снижение цены увеличивает реальный доход, и покупки некачественного товара сокращаются). В этом случае эффекты замены и дохода разнонаправлены. Наконец, если X ≈ товар Риффена,положительный эффект дохода перекрывает отрицательный эффект замены, так чтообщий результат изменения Р_X оказывается положительным, dХ/dР_X > 0 (повышение цены вызывает увеличение спроса на товар).

Очевидно, что изменение цены одного товара влияет на объем спроса не только данного, но и других товаров. Основываясь на ранее высказанных соображениях, мы можем разложить на эффект замены и эффект дохода и изменение объема спроса на товар Y в результате изменения цены товара X. Для этого модифицируем уравнение Слуцкого (3.17):

Левая часть (3.18) характеризует влияние изменения цены Р_X на объем спроса на товар Y. Правая представляет сумму эффектов дохода и замены. В случае двух товаров (X, Y) эффект замены, как следует из рис. 3.20, положителен. При неизменной полезности снижение ценыР_X приводит и к сокращению покупок товара Y (Y_S, Y_H < Y₁), что является следствием убывающей предельной нормы замены MRS.

Следовательно, общий результат dY/dР_X будет положительным или отрицательным в зависимости от сравнительной "силы" двух эффектов. На рис. 3.20 общий результат dY/dР_Xотрицателен, спрос на товар Y увеличивается с Y₁ до Y₂ в результате снижения Р_X на DР_X, поскольку отрицательный эффект дохода перекрывает положительный эффект замены.

Не нашли, что искали? Воспользуйтесь поиском по сайту: