Вероятность как нормированная мера
Определение. Пара 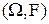 , в которой , в которой  - некоторое множество, а - некоторое множество, а
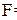 - -  -алгебра его подмножеств называется измеримым пространством. -алгебра его подмножеств называется измеримым пространством.
Определение. Пусть  - некоторое множество, - некоторое множество, 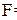 - -  -алгебра его подмножеств. Функция -алгебра его подмножеств. Функция 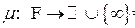 называется мерой на измеримом пространстве называется мерой на измеримом пространстве 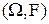 , если она удовлетворяет условиям: , если она удовлетворяет условиям:
М1) Для любого множества  его мера неотрицательна: его мера неотрицательна:  . .
М2) Для любого счетного набора попарно непересекающихся множеств  (то есть такого, что (то есть такого, что  ) мера их объединения равна сумме их мер: ) мера их объединения равна сумме их мер:  (счетная аддитивность или (счетная аддитивность или  -аддитивность). -аддитивность).
Другими словами, мера есть неотрицательная счетно-аддитивная функция множеств.
Определение. Пусть  - некоторое множество и - некоторое множество и 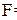 - -  -алгебра его подмножеств. Мера -алгебра его подмножеств. Мера 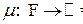 называется нормированной, если называется нормированной, если  . .
Определение. Пусть  - произвольное пространство элементарных событий и - произвольное пространство элементарных событий и 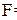 - -  -алгебра его подмножеств (событий). Вероятностью или вероятностной мерой на -алгебра его подмножеств (событий). Вероятностью или вероятностной мерой на 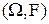 называется функция называется функция  , удовлетворяющая следующим аксиомам: , удовлетворяющая следующим аксиомам:
Р1). Аксиома неотрицательности:
Для любого события  выполняется неравенство: выполняется неравенство:  ; ;
Р2). Аксиома нормированности:
Вероятность достоверного события равна единице: 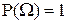 . .
Р3). Аксиома счетной аддитивности:
Для любой счетного набора попарно несовместных событий 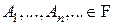  имеет место равенство: имеет место равенство:
 . .
Определение. Тройка 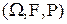 , в которой , в которой  - пространство элементарных событий, - пространство элементарных событий, 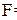 - -  -алгебра событий и -алгебра событий и  - вероятностная мера на - вероятностная мера на 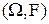 называется вероятностным пространством. называется вероятностным пространством.
Вероятностное пространство является математической моделью любых случайных явлений, изучаемых в теории вероятностей.
Проверка аксиомы счетной аддитивности Р3) на практике бывает весьма затруднительной. Для этого полезным оказывается следующее утверждение.
Теорема (доказательство см. Б.В. Гнеденко, Курс теории вероятностей).
Аксиома счетной аддитивности Р3) эквивалентна выполнению следующих двух аксиом Р3*) и Р4):
Р3*). Аксиома конечной аддитивности:
Для любого конечного набора событий 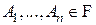 , являющихся попарно несовместными , являющихся попарно несовместными  , имеет место равенство: , имеет место равенство:
 . .
Р4). Аксиома непрерывности:
Если события 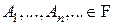 обладают свойствами: обладают свойствами:
1)  ; ;
2)  , ,
(при этом говорят, что события образуют убывающую последовательность), то
 . .
Из аксиоматического определения вероятности вытекают следующие свойства вероятности (здесь и везде в дальнейшем под знаком вероятности появляются только события!).
1°. 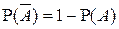 . .
2°.  . .
3°.  . .
4°. 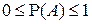 . .
(Свойства 1 – 4 были доказаны при рассмотрении классического определения вероятности сразу в общем случае).
5°. Теорема сложения вероятностей.
Для любых событий 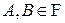 (не обязательно несовместных) (не обязательно несовместных)
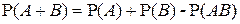 . .
▲ Представим событие В в виде:
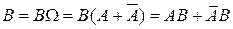 . .
Поскольку события  являются несовместными, то по аксиоме аддитивности Р3) являются несовместными, то по аксиоме аддитивности Р3)
 . (1) . (1)
Представим событие  в виде: в виде:
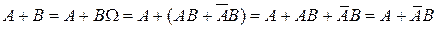 . .
Поскольку события  являются несовместными, то по аксиоме Р3) являются несовместными, то по аксиоме Р3)
 . (2) . (2)
Вычитая из равенства (2) равенство (1), получаем
 . ■ . ■
Задача. Доказать, что для любых трех событий А, В и С
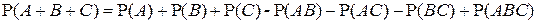 . .
Доказать общую формулу:
 . .
6°. Если события 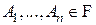 образуют полную группу событий, то образуют полную группу событий, то
 . .
▲ Свойство следует из определения полной группы событий и аксиом Р2) и Р3). ■
7°. 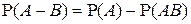 . .
▲ Представим событие А в виде:
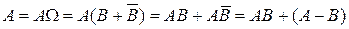 . .
Поскольку события  являются несовместными, то по аксиоме аддитивности Р3) являются несовместными, то по аксиоме аддитивности Р3)
 . ■ . ■
Покажем теперь, как на основе аксиоматического определения вероятности конструктивно можно задать вероятность для некоторых часто встречающихся на практике пространств элементарных событий, содержащих бесконечное число исходов.
Пусть пространство элементарных событий содержит счетное число исходов  . В качестве . В качестве  -алгебры событий -алгебры событий 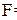 рассмотрим множество всех подмножеств рассмотрим множество всех подмножеств  . В этом случае любую вероятностную меру . В этом случае любую вероятностную меру  можно получить, задав вероятности исходов можно получить, задав вероятности исходов 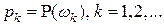 , причем последовательность , причем последовательность 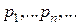 должна удовлетворять только условиям неотрицательности должна удовлетворять только условиям неотрицательности

и нормированности

(в этом и состоит основная идея аксиоматического определения вероятности).
Тогда, если вероятность любого события А определить как
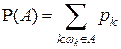 , ,
то она будет удовлетворять аксиомам Р1), Р2), Р3).
В частности, если пространство элементарных событий конечно 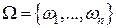 , а , а  (исходы равновозможны), то (исходы равновозможны), то

и мы приходим к классическому определению вероятности.
Предположим теперь, что пространство элементарных событий  , что соответствует эксперименту, состоящему в бросании наудачу точки на числовую прямую. В этом случае , что соответствует эксперименту, состоящему в бросании наудачу точки на числовую прямую. В этом случае  -алгебра событий должна содержать всевозможные открытые интервалы вида -алгебра событий должна содержать всевозможные открытые интервалы вида  , поскольку попадание точки в такие интервалы являются реальными событиями. В принципе существуют различные , поскольку попадание точки в такие интервалы являются реальными событиями. В принципе существуют различные  -алгебры, удовлетворяющие этому требованию. Но среди них есть одна -алгебры, удовлетворяющие этому требованию. Но среди них есть одна  -алгебра, элементы которой принадлежат всем остальным. Она является пересечением всех этих -алгебра, элементы которой принадлежат всем остальным. Она является пересечением всех этих  -алгебр и называется минимальной. Минимальная -алгебр и называется минимальной. Минимальная  -алгебра, содержащая множество всех интервалов на числовой прямой, называется борелевской -алгебра, содержащая множество всех интервалов на числовой прямой, называется борелевской  -алгеброй или -алгеброй или  -алгеброй борелевских множеств на числовой прямой и обозначается -алгеброй борелевских множеств на числовой прямой и обозначается 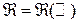 . .
Борелевская  -алгебра -алгебра  является достаточно богатой и содержит множества, перекрывающие любые потребности практики: является достаточно богатой и содержит множества, перекрывающие любые потребности практики:
- все открытые интервалы  принадлежат принадлежат  по определению; по определению;
- любые интервалы вида  также принадлежат также принадлежат  , поскольку, например, , поскольку, например,  , а все интервалы под знаком произведения принадлежат , а все интервалы под знаком произведения принадлежат  ; ;
- любые одноточечные множества  принадлежат принадлежат  , поскольку , поскольку  ; ;
- любые множества вида  , , 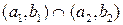 (включая результат выполнения счетного числа операций над ними), множество натуральных чисел (включая результат выполнения счетного числа операций над ними), множество натуральных чисел  , рациональных чисел , рациональных чисел  , иррациональных чисел , иррациональных чисел  , также принадлежат , также принадлежат  . .
Чтобы получить множество, не принадлежащее  , требуются специальные построения. , требуются специальные построения.
Замечание. Борелевская  -алгебра -алгебра  в в  строится совершенно так же, как в строится совершенно так же, как в  . .  является минимальной является минимальной  -алгеброй, содержащей все множества вида -алгеброй, содержащей все множества вида 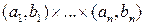 (уже не интервалы, как в (уже не интервалы, как в  , а прямоугольники в , а прямоугольники в  , параллелепипеды в , параллелепипеды в  и т.д.). и т.д.).
Для задания вероятностной меры на измеримом пространстве  можно взять произвольную неубывающую для любого можно взять произвольную неубывающую для любого 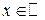 непрерывную слева функцию непрерывную слева функцию  , удовлетворяющую условиям: , удовлетворяющую условиям:
 , , 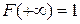 , ,
и каждому событию  поставить в соответствие вероятность поставить в соответствие вероятность
 , ,
а событию  - вероятность - вероятность
 . .
Определенная таким образом для всех событий  функция функция  будет удовлетворять аксиомам Р1), Р2), Р3). Для других событий из будет удовлетворять аксиомам Р1), Р2), Р3). Для других событий из  вероятность определяется единственным образом с помощью теоремы о продолжении меры (теорема Каратеодори, см. А.Н. Колмогоров, С.В. Фомин, Элементы функционального анализа или А.А. Боровков, Теория вероятностей). вероятность определяется единственным образом с помощью теоремы о продолжении меры (теорема Каратеодори, см. А.Н. Колмогоров, С.В. Фомин, Элементы функционального анализа или А.А. Боровков, Теория вероятностей).
Меру  , построенную по функции , построенную по функции 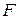 , называют вероятностной мерой Лебега-Стилтьеса, отвечающей функции , называют вероятностной мерой Лебега-Стилтьеса, отвечающей функции 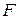 . .
Из той же теоремы о продолжении меры следует, что на измеримом пространстве  существует единственная мера существует единственная мера 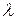 , значение которой на любом интервале равно его длине: , значение которой на любом интервале равно его длине:
 . .
Эта мера называется мерой Лебега.
Отсюда вытекает, что для любого множества  определена его длина (мера Лебега), так как А представимо в виде счетного числа операций над интервалами. Другими словами, любое борелевское множество на числовой прямой является измеримым. определена его длина (мера Лебега), так как А представимо в виде счетного числа операций над интервалами. Другими словами, любое борелевское множество на числовой прямой является измеримым.
Рассмотрим теперь случай, когда пространство элементарных событий  есть некоторое борелевское множество на числовой прямой, имеющее конечную меру Лебега есть некоторое борелевское множество на числовой прямой, имеющее конечную меру Лебега 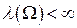 , что соответствует эксперименту, состоящему в бросании наудачу точки в множество , что соответствует эксперименту, состоящему в бросании наудачу точки в множество  . Обозначим . Обозначим 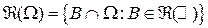 - -  -алгебру борелевских множеств множества -алгебру борелевских множеств множества  . Тогда, если вероятность любого события . Тогда, если вероятность любого события  определить как определить как
 , ,
то она будет удовлетворять аксиомам Р1), Р2), Р3) и мы приходим к геометрическому определению вероятности.
Если же множество  , то оно может не иметь длины (является неизмеримым) и вычислить вероятность попадания точки в данное множество в соответствии с геометрическим определением вероятности невозможно. , то оно может не иметь длины (является неизмеримым) и вычислить вероятность попадания точки в данное множество в соответствии с геометрическим определением вероятности невозможно.
Приведем пример множества на отрезке, мера Лебега которого не существует.
Пример (множество Витали).
Рассмотрим окружность единичного радиуса (реально это тот же отрезок 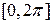 ). Возьмем любое иррациональное число ). Возьмем любое иррациональное число  . Поскольку оно иррационально, число . Поскольку оно иррационально, число  не является целым ни при каком целом не является целым ни при каком целом 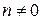 (то есть число (то есть число  равно равно  лишь при лишь при 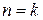 ). ).
Поэтому, если взять произвольную точку  , то есть точку на окружности, и перечислить все точки, которые получаются поворотом точки , то есть точку на окружности, и перечислить все точки, которые получаются поворотом точки  на угол на угол  , то мы ни разу не вернемся в точку , то мы ни разу не вернемся в точку  . Точек, получившихся из точки . Точек, получившихся из точки  такими поворотами, счетное число. Объединим их в один класс. С любой другой точкой окружности можно тоже связать класс точек, получающихся из нее поворотом на угол такими поворотами, счетное число. Объединим их в один класс. С любой другой точкой окружности можно тоже связать класс точек, получающихся из нее поворотом на угол  при каком-то при каком-то  . .
Таким образом, вся окружность разбивается на классы точек. В каждом классе счетное число точек, и все точки получаются друг из друга такими поворотами. Причем эти классы не пересекаются.
Множество  определим так: возьмем из каждого такого класса ровно по одной точке. Пусть множество определим так: возьмем из каждого такого класса ровно по одной точке. Пусть множество  получается поворотом всех точек множества получается поворотом всех точек множества  на угол на угол  . .
Так как все точки одного класса можно получить, поворачивая любую из них на угол  , а в множестве , а в множестве  собрано по одной точке из каждого класса, то поворачивая это множество, получим все точки окружности. собрано по одной точке из каждого класса, то поворачивая это множество, получим все точки окружности.
Очевидно, что  . Предположим, что мера Лебега (длина) множества . Предположим, что мера Лебега (длина) множества  существует. Заметим, что тогда все множества существует. Заметим, что тогда все множества  имеют ту же меру Лебега, так как получены из имеют ту же меру Лебега, так как получены из  поворотом. И так как все эти множества не пересекаются, то мера их объединения равна сумме их мер: поворотом. И так как все эти множества не пересекаются, то мера их объединения равна сумме их мер:
 . .
Полученное противоречие означает, что мера Лебега, или длина множества  не существует. не существует.
Условные вероятности
На практике случайные события обычно взаимосвязаны. Информация о наступлении одного из событий может влиять на шансы наступления другого. Пусть 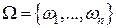 - конечное пространство равновозможных исходов, А и В – некоторые события. Если о событии В ничего неизвестно, то согласно классическому определению вероятности: - конечное пространство равновозможных исходов, А и В – некоторые события. Если о событии В ничего неизвестно, то согласно классическому определению вероятности:
 . .
Если же известно, что событие В уже произошло (т. е. наступил исход  , но какой именно – неизвестно), то для определения вероятности события А следует выбрать новое пространство элементарных событий , но какой именно – неизвестно), то для определения вероятности события А следует выбрать новое пространство элементарных событий 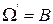 . .
В этом случае событию А благоприятствуют исходы  и новая вероятность, которую обозначим и новая вероятность, которую обозначим 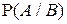 , равна: , равна:
 . .
Полученная вероятность называется условной вероятностью события А при условии, что событие В произошло и полученное для нее выражение в рамках классической схемы принимается за определение условной вероятности и в общем случае.
Определение. Пусть 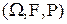 - произвольное вероятностное пространство, - произвольное вероятностное пространство, 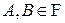 - некоторые случайные события, - некоторые случайные события,  . Условной вероятностью события А при условии, что событие В произошло, называется величина . Условной вероятностью события А при условии, что событие В произошло, называется величина
 . .
Для условной вероятности 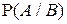 применяется также обозначение применяется также обозначение  . .
Условная вероятность 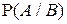 , как функция события А при фиксированном событии В (условии), удовлетворяет аксиомам Р1) – Р3) и, следовательно, всем свойствам вероятности, вытекающим из аксиом: , как функция события А при фиксированном событии В (условии), удовлетворяет аксиомам Р1) – Р3) и, следовательно, всем свойствам вероятности, вытекающим из аксиом:

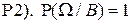
(Действительно,  ). ).
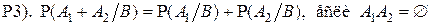
(Действительно,  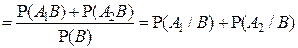 , ,
поскольку события  являются несовместными). являются несовместными).
Аналогично вводится понятие условной вероятности события В при условии, что событие А произошло:
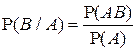
в предположении, что  . .
Если  и и  , то из определения условных вероятностей , то из определения условных вероятностей 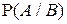 и и  получаем следующее правило умножения вероятностей: получаем следующее правило умножения вероятностей:
 . .
На случай любого конечного числа событий правило умножения вероятностей обобщается следующим образом.
Теорема (умножения вероятностей).
Пусть 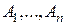 - некоторые события, определенные на одном и том же вероятностном пространстве - некоторые события, определенные на одном и том же вероятностном пространстве 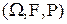 , для которых , для которых  . Тогда . Тогда
 . .
▲ В соответствии с правилом умножения вероятностей 
 . ■ . ■
Пример.
Партия из 100 деталей содержит 5 бракованных. Найти вероятность того, что среди отобранных 10 деталей не будет бракованных.
Решение. Рассмотрим события
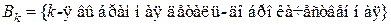 ; ;
 . .
Тогда 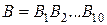 и в соответствии с теоремой умножения вероятностей получаем: и в соответствии с теоремой умножения вероятностей получаем:
 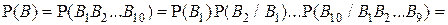
 . .
Заметим, что тот же ответ получается и при использовании классического определения вероятности:
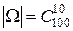 , , 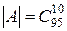 и и 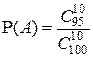 = 0,584 (см. пример Урновая схема). = 0,584 (см. пример Урновая схема).
Не нашли, что искали? Воспользуйтесь поиском по сайту:
©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|


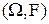 , в которой
, в которой  - некоторое множество, а
- некоторое множество, а 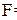 -
-  -алгебра его подмножеств называется измеримым пространством.
-алгебра его подмножеств называется измеримым пространством.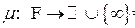 называется мерой на измеримом пространстве
называется мерой на измеримом пространстве  его мера неотрицательна:
его мера неотрицательна:  .
. (то есть такого, что
(то есть такого, что  ) мера их объединения равна сумме их мер:
) мера их объединения равна сумме их мер:  (счетная аддитивность или
(счетная аддитивность или 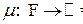 называется нормированной, если
называется нормированной, если  .
. , удовлетворяющая следующим аксиомам:
, удовлетворяющая следующим аксиомам: ;
;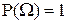 .
.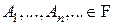
 имеет место равенство:
имеет место равенство: .
.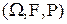 , в которой
, в которой  - вероятностная мера на
- вероятностная мера на 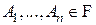 , являющихся попарно несовместными
, являющихся попарно несовместными  .
. ;
; ,
, .
.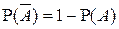 .
. .
. .
.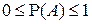 .
.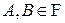 (не обязательно несовместных)
(не обязательно несовместных)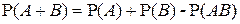 .
.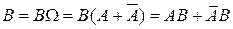 .
. являются несовместными, то по аксиоме аддитивности Р3)
являются несовместными, то по аксиоме аддитивности Р3) . (1)
. (1) в виде:
в виде: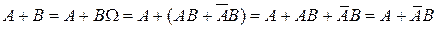 .
. являются несовместными, то по аксиоме Р3)
являются несовместными, то по аксиоме Р3) . (2)
. (2) . ■
. ■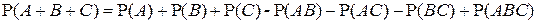 .
. .
. .
.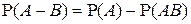 .
.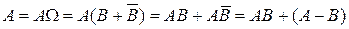 .
. являются несовместными, то по аксиоме аддитивности Р3)
являются несовместными, то по аксиоме аддитивности Р3) . ■
. ■ . В качестве
. В качестве 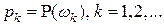 , причем последовательность
, причем последовательность 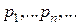 должна удовлетворять только условиям неотрицательности
должна удовлетворять только условиям неотрицательности

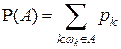 ,
,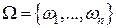 , а
, а  (исходы равновозможны), то
(исходы равновозможны), то
 , что соответствует эксперименту, состоящему в бросании наудачу точки на числовую прямую. В этом случае
, что соответствует эксперименту, состоящему в бросании наудачу точки на числовую прямую. В этом случае  , поскольку попадание точки в такие интервалы являются реальными событиями. В принципе существуют различные
, поскольку попадание точки в такие интервалы являются реальными событиями. В принципе существуют различные 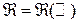 .
. является достаточно богатой и содержит множества, перекрывающие любые потребности практики:
является достаточно богатой и содержит множества, перекрывающие любые потребности практики: принадлежат
принадлежат  также принадлежат
также принадлежат  , а все интервалы под знаком произведения принадлежат
, а все интервалы под знаком произведения принадлежат  принадлежат
принадлежат  ;
; ,
, 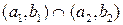 (включая результат выполнения счетного числа операций над ними), множество натуральных чисел
(включая результат выполнения счетного числа операций над ними), множество натуральных чисел  , рациональных чисел
, рациональных чисел  , иррациональных чисел
, иррациональных чисел  , также принадлежат
, также принадлежат  в
в  строится совершенно так же, как в
строится совершенно так же, как в  .
. 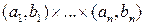 (уже не интервалы, как в
(уже не интервалы, как в  , параллелепипеды в
, параллелепипеды в  и т.д.).
и т.д.). можно взять произвольную неубывающую для любого
можно взять произвольную неубывающую для любого 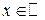 непрерывную слева функцию
непрерывную слева функцию  , удовлетворяющую условиям:
, удовлетворяющую условиям: ,
, 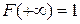 ,
, поставить в соответствие вероятность
поставить в соответствие вероятность ,
, - вероятность
- вероятность .
. будет удовлетворять аксиомам Р1), Р2), Р3). Для других событий из
будет удовлетворять аксиомам Р1), Р2), Р3). Для других событий из 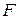 , называют вероятностной мерой Лебега-Стилтьеса, отвечающей функции
, называют вероятностной мерой Лебега-Стилтьеса, отвечающей функции 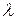 , значение которой на любом интервале равно его длине:
, значение которой на любом интервале равно его длине: .
. определена его длина (мера Лебега), так как А представимо в виде счетного числа операций над интервалами. Другими словами, любое борелевское множество на числовой прямой является измеримым.
определена его длина (мера Лебега), так как А представимо в виде счетного числа операций над интервалами. Другими словами, любое борелевское множество на числовой прямой является измеримым. есть некоторое борелевское множество на числовой прямой, имеющее конечную меру Лебега
есть некоторое борелевское множество на числовой прямой, имеющее конечную меру Лебега 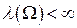 , что соответствует эксперименту, состоящему в бросании наудачу точки в множество
, что соответствует эксперименту, состоящему в бросании наудачу точки в множество 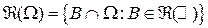 -
-  определить как
определить как ,
, , то оно может не иметь длины (является неизмеримым) и вычислить вероятность попадания точки в данное множество в соответствии с геометрическим определением вероятности невозможно.
, то оно может не иметь длины (является неизмеримым) и вычислить вероятность попадания точки в данное множество в соответствии с геометрическим определением вероятности невозможно.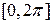 ). Возьмем любое иррациональное число
). Возьмем любое иррациональное число  . Поскольку оно иррационально, число
. Поскольку оно иррационально, число  не является целым ни при каком целом
не является целым ни при каком целом 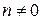 (то есть число
(то есть число  равно
равно  лишь при
лишь при 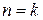 ).
). , то есть точку на окружности, и перечислить все точки, которые получаются поворотом точки
, то есть точку на окружности, и перечислить все точки, которые получаются поворотом точки  на угол
на угол  , то мы ни разу не вернемся в точку
, то мы ни разу не вернемся в точку  .
. определим так: возьмем из каждого такого класса ровно по одной точке. Пусть множество
определим так: возьмем из каждого такого класса ровно по одной точке. Пусть множество  получается поворотом всех точек множества
получается поворотом всех точек множества  . Предположим, что мера Лебега (длина) множества
. Предположим, что мера Лебега (длина) множества  .
. , но какой именно – неизвестно), то для определения вероятности события А следует выбрать новое пространство элементарных событий
, но какой именно – неизвестно), то для определения вероятности события А следует выбрать новое пространство элементарных событий 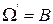 .
.  и новая вероятность, которую обозначим
и новая вероятность, которую обозначим 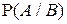 , равна:
, равна: .
. . Условной вероятностью события А при условии, что событие В произошло, называется величина
. Условной вероятностью события А при условии, что событие В произошло, называется величина .
. .
.
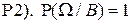
 ).
).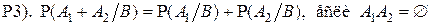

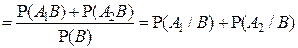 ,
,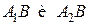 являются несовместными).
являются несовместными).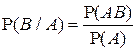
 .
. получаем следующее правило умножения вероятностей:
получаем следующее правило умножения вероятностей: .
.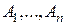 - некоторые события, определенные на одном и том же вероятностном пространстве
- некоторые события, определенные на одном и том же вероятностном пространстве  . Тогда
. Тогда .
.
 . ■
. ■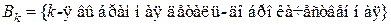 ;
; .
.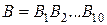 и в соответствии с теоремой умножения вероятностей получаем:
и в соответствии с теоремой умножения вероятностей получаем:
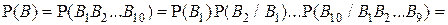
 .
.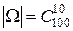 ,
, 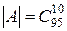 и
и 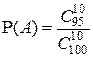 = 0,584 (см. пример Урновая схема).
= 0,584 (см. пример Урновая схема).