
|
|
Признаки возрастания и убывания функции.Теорема 1 (признак возрастания функции). Если дифференцируемая функция Теорема 2 (признак убывания функции). Если дифференцируемая функция Обратные теоремы также справедливы. Теорема 3 (признак возрастания функции). Если производная функции положительна на некотором интервале, то функция на этом интервале монотонно возрастает. Теорема 4 (признак убывания функции). Если производная функции отрицательна на некотором интервале, то функция на этом интервале монотонно убывает.
Если функция возрастает, то
Если функция убывает, то Такие рассуждения приводят к выводу: на промежутке монотонности (возрастания или убывания) производная свой знак не меняет. Изменение характера монотонности происходит при изменении знака производной
Из этих рассуждений следует правило нахождения промежутков монотонности.
Правило исследования функции на монотонность 1. Найти производную функции 2. Найти точки, в которых производная Эти точки называются критическими точками для функции 3. Отметить критические точки на числовой прямой и определить знак производной 4. По полученным знакам производной сделать вывод о характере монотонности: если если П р и м е р. Найти промежутки монотонности функции Решение. 1) Найдём производную функции
2)Найдём критические точки
Решив уравнение, получим 3) Отметим критические точки на числовой прямой и определим знак производной
-1 2 4) Вывод: функция возрастает при функция убывает при Вопросы для самопроверки 1. Сформулируйте признак (прямой и обратный) возрастания функции. 2. Сформулируйте признак (прямой и обратный) убывания функции. 3. Как связаны монотонность функции и угол наклона касательной к графику этой функции? 4. Какие точки называются критическими для функции? 5. Сформулируйте правило исследования функции на монотонность.
Упражнения Исследовать функции на монотонность: 1. 3. 5.
Урок № 13 Тема урока:ИССЛЕДОВАНИЕ ФУНКЦИИ НА ЭКСТРЕМУМ ПО ПЕРВОЙ И ВТОРОЙ ПРОИЗВОДНОЙ. Определение точек экстремума. Рассмотрим график функции
В точках В точках Вот такие точки функции и называются точками максимума и минимума. Определение 1. Точка Определение 2. Точка Значения функции Максимум и минимум функции объединяют названием экстремумы функции. Точки максимума и минимума называются точками экстремума (или экстремальными точками). Надо отметить, что максимум функции не всегда является наибольшим значением во всей области определения функции, он является наибольшим лишь по сравнению со значениями функции, взятыми в некоторой окрестности этой точки.

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 возрастает на данном интервале, то производная этой функции не отрицательна на этом интервале.
возрастает на данном интервале, то производная этой функции не отрицательна на этом интервале. 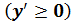







 Эти утверждения можно пояснить геометрически.
Эти утверждения можно пояснить геометрически.








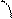


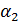

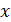
 и
и  , а это возможно только при
, а это возможно только при . Следовательно, угол наклона касательной – острый.
. Следовательно, угол наклона касательной – острый. и
и  , а это возможно только при
, а это возможно только при  . Следовательно, угол наклона касательной – тупой.
. Следовательно, угол наклона касательной – тупой. . А это возможно лишь при переходе производной через ноль
. А это возможно лишь при переходе производной через ноль  или через точку, в которой производная не существует (точка
или через точку, в которой производная не существует (точка  .
.
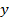







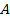
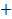
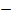
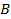
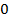


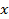
 .
. или
или 
 , то функция возрастает;
, то функция возрастает; , то функция убывает.
, то функция убывает. .
.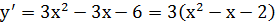
 , если 3
, если 3  или
или 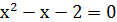 (разделили на 3).
(разделили на 3). и
и  .
.






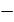





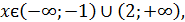
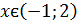
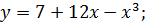 2.
2. 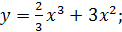
 4.
4. 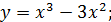
 ; 6.
; 6. 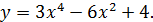
 , изображённый на рисунке.
, изображённый на рисунке. Рис.1
Рис.1 функция переходит от возрастания к убыванию и в этих точках функция
функция переходит от возрастания к убыванию и в этих точках функция 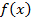 принимает наибольшие значения по сравнению с рядом лежащими точками.
принимает наибольшие значения по сравнению с рядом лежащими точками. функция переходит от убывания к возрастанию и в этих точках функция
функция переходит от убывания к возрастанию и в этих точках функция  называется точкой максимума функции
называется точкой максимума функции  , если для всех
, если для всех  взятых из некоторой окрестности точки
взятых из некоторой окрестности точки 

 в точках максимума и минимума называются соответственно максимумомиминимумом функции.
в точках максимума и минимума называются соответственно максимумомиминимумом функции. Рис. 2
Рис. 2