
|
|
Понятие касательной и нормали к кривойМы знаем аналитический и физический смысл производной: аналитический смысл – это Для этого введём понятие касательной к кривой в данной точке. Из школьного курса геометрии, вы знаете понятие касательной к окружности. Касательная к окружности определяется как прямая, лежащая в одной плоскости с окружностью и имеющая с ней единственную общую точку.
M1 Дадим общее определение касательной к M2 кривой в данной точке. М3 Пусть К При приближении точки
Определение.Предельное положение секущей Определение. Нормалью к кривой в точке
Геометрический смысл производной Пусть кривая лежат на графике функции. Прямая
0
Производная функции Уравнение касательной к кривой Уравнение нормалик кривой РЕШЕНИЕ ЗАДАЧ П р и м е р 1. Вычислите угловые коэффициенты касательных к параболе Решение. Из геометрического смысла производной (формула 1) угловой коэффициент касательной Найдём производную функции: 1) Найдём значение производной в точке
2) Найдём значение производной в точке
П р и м е р 2. У параболы Решение. По формуле (1) Найдём 1) Вычислим значение производной в точке Следовательно, 2) Аналогично в точке Следовательно, П р и м е р 3. В какой точке касательная к кривой под углом Решение. По формуле (1)
Подставив П р и м е р 4. Составить уравнение касательной и нормали к параболе Решение. Уравнение касательной к кривой имеет вид Из условия задачи
Подставив все значения в уравнение
Составим уравнение нормали, воспользовавшись формулой
Вопросы для самопроверки 1. Дайте определение касательной к кривой. 2. Что называется нормалью к кривой? 3. В чём заключается геометрический смысл производной? Запишите формулу. 4. Запишите уравнение касательной к кривой в данной точке. 5. Запишите уравнение нормали к кривой в данной точке.
Задачи для самостоятельного решения 1. Найти угловой коэффициент касательной, проведённой к кривой в точке 2. Кривая задана уравнением 3. На кривой 4. В какой точке касательная к кривой 5. Найти абсциссу точки параболы 6. Найти угловой коэффициент касательной, проведённой к кривой в точке 7. В какой точке касательная к кривой 8. В какой точке касательная к графику функции с осью 9. В какой точке касательная к графику функции 10. В каких точках угловой коэффициент касательной к кубической параболе 11. Найти угол наклона касательной к кривой 12. Составить уравнение касательной к параболе 13. Составить уравнение касательной к гиперболе 14. Составить уравнение касательной к кривой 15. Найти касательную к кривой
Урок № 12 Т е м а. ИССЛЕДОВАНИЕ ФУНКЦИИ НА МОНОТОННОСТЬ С ПОМОЩЬЮ ПРОИЗВОДНОЙ Рассмотрим приложение производной к исследованию функции на возрастание и убывание. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 , физический – это скорость процесса, заданного функцией. Выясним геометрический смысл производной.
, физический – это скорость процесса, заданного функцией. Выясним геометрический смысл производной.



 Но такое определение касательной неприменимо для случая произвольной кривой. Например, для параболы
Но такое определение касательной неприменимо для случая произвольной кривой. Например, для параболы 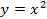 оси
оси  имеют по одной общей точке с параболой. Однако ось
имеют по одной общей точке с параболой. Однако ось 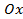 является касательной к параболе, а ось
является касательной к параболе, а ось  – нет.
– нет. – некоторые точки произвольной кривой
– некоторые точки произвольной кривой  – секущая кривой.
– секущая кривой. по кривой секущая
по кривой секущая  будет поворачиваться вокруг точки
будет поворачиваться вокруг точки 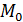 , занимая положения
, занимая положения  ,
, 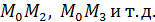
 при неограниченном приближении точки
при неограниченном приближении точки 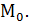
 называется прямая, проходящая через точку
называется прямая, проходящая через точку  перпендикулярно касательной к кривой в этой точке.
перпендикулярно касательной к кривой в этой точке.
 Если
Если 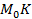 – касательная к кривой
– касательная к кривой 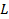 в точке
в точке  ,
, то
то  перпендикулярная
перпендикулярная 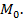
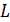
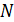
 . Точки
. Точки 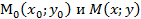
 - секущая кривой
- секущая кривой 





 - угол наклона касательной
- угол наклона касательной
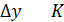


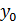






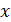
 в точке
в точке 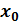 равна тангенсу угла наклона касательной, проведённой в точке
равна тангенсу угла наклона касательной, проведённой в точке 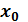 или угловому коэффициенту касательной к графику функции в этой точке.
или угловому коэффициенту касательной к графику функции в этой точке. 
 в точке
в точке  имеет вид
имеет вид

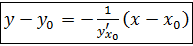

 в точках
в точках  .
. .
. .
.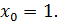
 . Следовательно,
. Следовательно,  .
.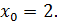
 . Следовательно,
. Следовательно,  .
.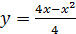 проведены касательные в точках
проведены касательные в точках  Найдите углы наклона касательных к оси Ох.
Найдите углы наклона касательных к оси Ох.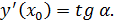
 .
.  .
. :
: 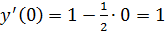 .
. и
и  .
.
 .
. и
и 
 наклонена к оси Ох
наклонена к оси Ох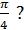
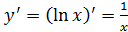 ;
;  . Следовательно,
. Следовательно, 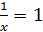 и
и 
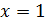 в функцию
в функцию  . Получили точку
. Получили точку  .
. в точке
в точке 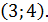
 .
.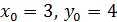 . Найдём производную
. Найдём производную  ;
;  .
. получим уравнение касательной
получим уравнение касательной или
или  .
. или
или 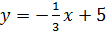
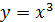
 .
. Определить углы наклона касательных к положительному направлению оси
Определить углы наклона касательных к положительному направлению оси  , проведённых к кривой в точках в точках с абсциссами
, проведённых к кривой в точках в точках с абсциссами 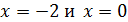 .
. найти точку, в которой касательная параллельна прямой
найти точку, в которой касательная параллельна прямой  .
.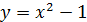 : а) параллельна оси
: а) параллельна оси 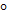 ?
? , в которой касательная параллельна оси абсцисс.
, в которой касательная параллельна оси абсцисс.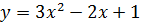
 .
. образует с осью
образует с осью  образует угол 135
образует угол 135  параллельна оси абсцисс?
параллельна оси абсцисс? в точке, абсцисса которой равна 2.
в точке, абсцисса которой равна 2. в точке с абсциссой
в точке с абсциссой  в точке
в точке 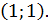
 в точке
в точке  .
. в точке с абсциссой
в точке с абсциссой