
|
|
ГЕОМЕТРИЧЕСКИЙ СМЫСЛ ПРОИЗВОДНОЙПОНЯТИЕ ВТОРОЙ ПРОИЗВОДНОЙ. Механическое истолкование производной было впервые дано И. Ньютоном. Оно заключается в следующем. Физический смысл первой производной Производная y П р и м е р 1. Точка движется прямолинейно по закону Решение. Скорость прямолинейного движения равна производной пути по времени, то есть Подставив в уравнение скорости П р и м е р 2. Маховик, задерживаемый тормозом, поворачивается за t с на угол
а) угловую скорость вращения маховика в момент t = 6 с; б) в какой момент времени маховик остановится? Решение. а) Угловая скорость вращения маховика определяется по формуле Подставляя t = 6 с, получим б) В тот момент, когда маховик остановится, его скорость будет равна нулю П р и м е р 3. Тело массой 6 кг движется прямолинейно по закону Решение. Найдём скорость движения тела в любой момент времени t.
Вычислим скорость тела в момент времени Определим кинетическую энергию тела в момент времени
Производная второго порядка. Производная n-го порядка. Производная от данной функции называется первой производной или производной первого порядка. Но производная функции также является функцией, и если она дифференцируема, то от неё, в свою очередь, можно найти производную. Производная от производной называется второй производной или производной второго порядка и обозначается Производная от второй производной называется производной третьего порядка и обозначается Примеры. 1)
Механический смысл второй производной. Если первая производная функции – это мгновенная скорость изменения любого процесса, заданного функцией, то вторая производная – это скорость изменения скорости, то есть ускорение, то есть Итак, первая производная – это скорость изменения процесса, вторая производная – ускорение. Пример 4. Точка движется прямолинейно по закону Решение. Найдём скорость точки в любой момент времени t.
Вычислим скорость в момент времени
Найдём ускорение точки в любой момент времени t.
Пример 5. Тело массой 3 кг движется прямолинейно по закону Решение. Сила, действующая на тело, находится по формуле Найдём скорость движения точки в любой момент времени t.
Тогда Найдём ускорение: Тогда Вопросы для самопроверки 1. В чём заключается физический смысл первой производной? 2. Как найти мгновенную скорость прямолинейного неравномерного движения? Запишите формулу. 3. Что называется производной второго порядка, третьего порядка, n-го порядка? 4. В чём заключается механический смысл производной? 5.Как найти ускорение прямолинейного неравномерного движения в данный момент времени? Запишите формулу.
Урок № 10 Т е м а. ПРИЛОЖЕНИЕ ПРОИЗВОДНОЙ К РЕШЕНИЮ ПРИКЛАДНЫХ ЗАДАЧ Решите задачи. 1. Путь, пройденный материальной точкой, задаётся уравнением
2. Вычислить ускорение материальной точки в конце 3-й секунды, если точка движется по закону 3. Точка движется прямолинейно по закону 4. Материальная точка движется прямолинейно по закону 5. Путь, пройденный клетью подъёмной машины, определяется уравнением
6. Определить момент 7. Закон движения частицы определяется уравнением 8. Температура тела T изменяется в зависимости от времени t по закону
9. Количество электричества, протекающего через проводник, задаётся формулой 10. Сила тока изменяется в зависимости от времени по закону 11. Известно, что тело массой m = 5кг движется прямолинейно по закону 12. Две материальные точки движутся прямолинейно по законам: 13. Две материальные точки движутся прямолинейно по законам: 14. Основание а параллелограмма изменяется по закону 15. Радиус круга R изменяется по закону 16. Материальная точка массой 2кг движется прямолинейно по закону
17. Маховик, задерживаемый тормозом, поворачивается за t секунд на угол а) угловую скорость вращения маховика в момент t = 6с; б) в какой момент маховик остановится? 18. Материальная точка движется прямолинейно по закону где s – путь в метрах, t – время в секундах. Найдите: а) момент времени t, когда ускорение точки равно 0; б) скорость, с которой движется точка в этот момент времени.
Урок № 11 Т е м а.ПОНЯТИЕ КАСАТЕЛЬНОЙ И НОРМАЛИ. ГЕОМЕТРИЧЕСКИЙ СМЫСЛ ПРОИЗВОДНОЙ 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 функции
функции  – это мгновенная скорость изменения этой функции. В частности, если зависимость между пройденным путём
– это мгновенная скорость изменения этой функции. В частности, если зависимость между пройденным путём  и временем
и временем  при прямолинейном неравномерном движении выражается уравнением
при прямолинейном неравномерном движении выражается уравнением  , то для нахождения мгновенной скорости точки в какой-нибудь определённый момент времени
, то для нахождения мгновенной скорости точки в какой-нибудь определённый момент времени  и подставить в неё соответствующее значение
и подставить в неё соответствующее значение 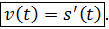
 (s выражается в метрах, t – в секундах). Найти скорость движения через 3 секунды после начала движения.
(s выражается в метрах, t – в секундах). Найти скорость движения через 3 секунды после начала движения.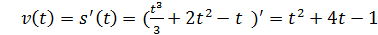 .
. с, получим
с, получим 
 (t) = 4t – 0,2t2 (рад). Найдите:
(t) = 4t – 0,2t2 (рад). Найдите: Тогда
Тогда 
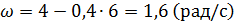 .
. . Поэтому
. Поэтому  . Отсюда
. Отсюда 
 Найти кинетическую энергию тела
Найти кинетическую энергию тела  через 3 с после начала движения.
через 3 с после начала движения.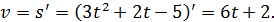

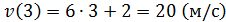 .
.

 .
. Производную n-го порядка обозначают
Производную n-го порядка обозначают  или
или 
 2)
2) 

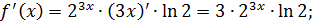
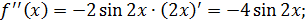
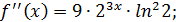



 .
.

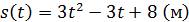 . Найти скорость и ускорение точки в момент
. Найти скорость и ускорение точки в момент  .
.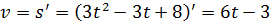
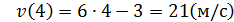
 и
и  , то есть ускорение в этом случае является величиной постоянной.
, то есть ускорение в этом случае является величиной постоянной.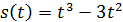 +5. Найти силу, действующую на тело в момент времени
+5. Найти силу, действующую на тело в момент времени 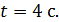

 .
. .
. =
= 
 .
.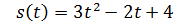 . Найти скорость и ускорение точки в конце 5-й секунды.
. Найти скорость и ускорение точки в конце 5-й секунды. .
.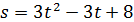 . Найти скорость и ускорение точки в момент
. Найти скорость и ускорение точки в момент 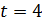 секунды.
секунды. . Найти её ускорение в конце 3-й секунды.
. Найти её ускорение в конце 3-й секунды. . Найти скорость и ускорение в момент времени 5 с.
. Найти скорость и ускорение в момент времени 5 с. , равно нулю. Какова при этом скорость?
, равно нулю. Какова при этом скорость? . Каково ускорение частицы в момент, когда её скорость равна 11 м/с?
. Каково ускорение частицы в момент, когда её скорость равна 11 м/с?
 . С какой скоростью нагревается это тело в момент времени
. С какой скоростью нагревается это тело в момент времени  ?
?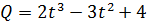 . Найти силу тока в конце 4-й секунды.
. Найти силу тока в конце 4-й секунды. (I – в амперах, t – в секундах). Найти скорость изменения силы тока в конце 8-й секунды.
(I – в амперах, t – в секундах). Найти скорость изменения силы тока в конце 8-й секунды.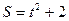 . Найдите кинетическую энергию тела
. Найдите кинетическую энергию тела 
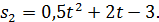 В какой момент времени скорости их равны?
В какой момент времени скорости их равны?
 В какой момент времени скорость первой точки будет в два раза больше скорости второй?
В какой момент времени скорость первой точки будет в два раза больше скорости второй?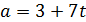 , а высота
, а высота  по закону
по закону  Вычислите скорость изменения его площади
Вычислите скорость изменения его площади  в момент t = 4c. (Основание а и высота b измеряются в сантиметрах).
в момент t = 4c. (Основание а и высота b измеряются в сантиметрах).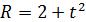 . C какой скоростью изменяется его площадь в момент
. C какой скоростью изменяется его площадь в момент  , если радиус круга измеряется в сантиметрах.
, если радиус круга измеряется в сантиметрах. , где s- путь в метрах, t – время в секундах. Найдите силу, действующую на неё в момент t = 3 c.
, где s- путь в метрах, t – время в секундах. Найдите силу, действующую на неё в момент t = 3 c. 
 (рад). Найдите:
(рад). Найдите: ,
,