
|
|
График плотности распределения называется кривой распределения.Свойства плотности распределения.
Если между двумя случайными величинами Х и Y существует функциональная зависимость Y=φ(Х), то взаимосвязь между плотностями распределения р(х) и р(у) задается формулой
Действительно, пусть с ростом Х растет Y. Тогда F(x)=F(y)=F(φ(x)) (см. свойства функции распределения). По правилу дифференцирования сложной функции находим
или, поскольку y = φ(x),
В случае, если с ростом Х величина Y убывает, первая производная dy/dx < 0, но плотность p(x) > 0. Поэтому в общем случае первая производная берется по абсолютной величине. Рассмотрим примеры.
Пример 1. Из равенства функций распределения F(x) = F(lnx) требуется найти соотношение между плотностями p(x) и p(lnx). Дифференцируя последнее равенство по x, имеем:
откуда xp(x) = p(lnx). Числовые характеристики случайных величин: показатели положения и рассеяния.
Для возможно более полного и всестороннего описания случайных величин используют различные показатели. К ним относятся: – характеристики положения – математическое ожидание, мода, медиана; – характеристики вариации – дисперсия, среднее квадратическое отклонение, коэффициент вариации; – характеристики формы распределения – коэффициенты асимметрии и островершинности, которые выражаются через моменты. Математическое ожидание непрерывной случайной величины Х задается интегралом
Свойства математического ожидания непрерывной случайной величины те же, что и дискретной случайной величины. Мода – такое значение случайной величины, при котором плотность максимальна. Медиана (Ме) случайной величины Х определяется соотношением P(X<Me)=P(X>Me). Она делит площадь под кривой распределения пополам. Дисперсия непрерывной случайной величины Х задается формулой
где Коэффициент вариации
– выраженное в процентах отношение среднего квадратического отклонения случайной величины Х к ее математическому ожиданию. Центральные моменты r-го порядка (r = 2, 3, 4) задаются формулой
Заметим, что Коэффициент асимметрии (скошенность)
Коэффициент островершинности (эксцесс)
Ниже будут использоваться первые определения величин Числовые характеристики дискретной случайной величины
Математическое ожидание Математическое ожидание дискретной случайной величины равно сумме произведений всех ее возможных значений на их вероятности
Математическое ожидание есть неслучайная (постоянная) величина. Пример 1. Найти математическое ожидание случайной величины Х по ее закону распределения:
Решение. Пример 2. Найти математическое ожидание числа появлений события А в одном испытании, если вероятность события А равна р. Решение. Случайная величина Х – число появлений события А в одном испытании – может принимать два значения: х1 =1 (событие наступило) с вероятностью р и х2 = 0 (событие не наступило) с вероятностью 1–р=q. Следовательно,
т.е. математическое ожидание числа появлений события в одном испытании равно вероятности этого события. Оценкой математического ожидания является среднее арифметическое наблюденных значений случайной величины. Свойства математического ожидания Приведем без доказательства основные свойства математического ожидания. 1. М(С)=С – математическое ожидание постоянной величины С равно значению самой постоянной. 2. М(СХ)=СМ(Х) – постоянную величину можно выносить за знак математического ожидания. 3. М(ХY)=М(Х)М(Y) – для двух независимых случайных величин математическое ожидание произведения равно произведению их математических ожиданий. 4. М(Х+Y)=M(X)+M(Y) – для двух случайных величин (зависимых или независимых) математическое ожидание суммы равно сумме математических ожиданий слагаемых. Математическое ожидание числа появлений события А в n независимых испытаниях равно произведению числа испытаний n на вероятность появления события в каждом испытании р, т.е. М(Х)=nр. Доказательство свойств математического ожидания см., например, в учебниках [3,4]. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
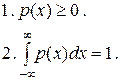
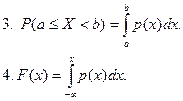
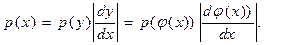
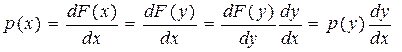
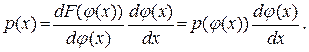

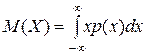 .
.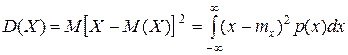 ,
,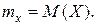
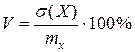
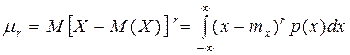 .
.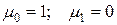 .
.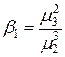 или
или 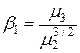 .
.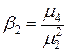 или
или 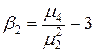 .
.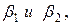 введенные К.Пирсоном.
введенные К.Пирсоном.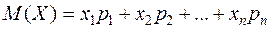 .
.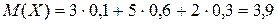 .
.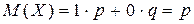 ,
,