
|
|
Технические аналоги булевых функций.Техническим аналогом булевой функции является комбинационная схема, выполняющая соответствующее этой функции преобразование информации. Провод, по которому в схеме передается двоичный сигнал, может рассматриваться как технический аналог булевой переменной, а уровни напряжения шин, соответствующие принятому в схеме представлению сигналов 0 и Элементарные логические операции над двоичными переменными реализуются электронными схемами, которые называются электронными логическими элементами или просто логическими элементами. Число входов логического элемента соответствует числу аргументов воспроизводимой им булевой функции. Один и тот же закон преобразования информации можно реализовать, используя различные типы и комбинации логических элементов и различные связи между ними. Для набора логических элементов можно ввести понятие функциональной полноты. Набор логических элементов обладает функциональной полнотой, если при помощи конечного числа этих элементов можно построить схему с любым законом функционирования. Любая комбинационная схема может быть построена с применением лишь трех видов логических элементов (технических аналогов булевых функций – дизъюнкции, конъюнкции, инверсии): элемента ИЛИ, элемента И, элемента НЕ соответственно. Следовательно, совокупность элементов ИЛИ, И, НЕ является функционально полной системой. Функционально полной системой является также система, состоящая из одиночного элемента И-НЕ (элемент Шеффера) или одиночного элемента ИЛИ-НЕ (элемент Пирса), или одиночного элемента И-ИЛИ-НЕ. На основе элемента Шеффера можно получить, используя законы алгебры логики, три основные логические функции ИЛИ, И, НЕ, составляющие основной функционально полный набор (ОФПН) функций.
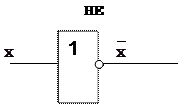
На рис.1.1 приведены условные графические обозначения (УГО) основных логических элементов: ИЛИ, И, НЕ, ИЛИ-НЕ, И-НЕ, И-ИЛИ-НЕ, используемых при синтезе комбинационных схем.
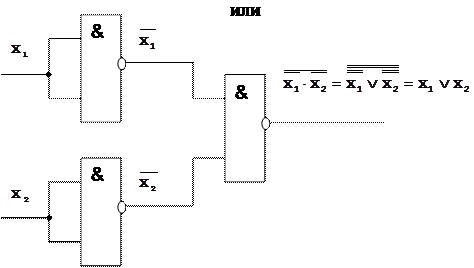
Рис.1.1 УГОлогических элементов: ИЛИ, И, НЕ, ИЛИ-НЕ, И-НЕ, И-ИЛИ-НЕ. Функциональная полнота системы элементов И-НЕ иллюстрируется на рис.1.2.
Рис.1.2
Аналогично можно показать функциональную полноту системы элементов ИЛИ-НЕ; И-ИЛИ-НЕ.
Синтез комбинационных схем. Существуют различные способы задания или представления булевых функций: 1. Словесное представление функций. Например: функция от трех аргументов принимает значение 1, если два любых аргумента или все три равны 1. Во всех других случаях функция равна 0. Этим высказыванием значения выходной функции соответствующей схемы полностью задано. 2. Табличный способ. При этом способе функция представляется в виде таблицы истинности, в которой записываются все возможные наборы аргументов и для каждого набора устанавливается значение функции 0 и 1. 3. Алгебраический способ. От таблицы истинности можно перейти к алгебраической форме представления функции. В такой форме удобно производить различные преобразования функций, например, с целью их минимизации. Дизъюнктивная нормальная форма (ДНФ) представляет собой логическую сумму элементарных логических произведений, в каждое из которых аргумент или его отрицание входят не более одного раза.
Если каждое слагаемое содержит все переменные или их отрицания, то в этом случае логическая функция представлена в совершенной дизъюнктивной нормальной форме (СДНФ). Конъюнктивная нормальная форма (КНФ) представляет собой логическое произведение элементарных логических сумм, в каждую из которых аргумент или его отрицание входят не более одного раза.
Переход от таблицы истинности к СДНФ можно осуществить следующим путем. Для каждого набора, на котором функция равна единице, записывается произведение всех аргументов, причем, если аргумент в этом наборе принимает значение "0", то пишется его отрицание. Затем производится логическое сложение этих элементарных произведений. Для перехода от таблицы истинности к СКНФ логической функции, по каждому набору двоичных переменных, на котором функция принимает значение “0”, записывается дизъюнкция всех переменных, и полученные дизъюнкции логически перемножаются. При записи логических сумм инвертируются те переменные, которые в таблице истинности имеют значение единицы. Пример написания СДНФ и СКНФ логической функции. Пусть логические функции у1 и у2 заданы в виде таблицы истинности, табл.1.3. Таблица.1.3.
Тогда СДНФ и СКНФ логических функций у1 и у2 запишутся следующим образом:
Комбинационные схемы, реализующие вышеприведенные СДНФ и СКНФ логических функций, должны содержать, рис.1.3 – 1.6 соответственно: У1сднф–четыре трехвходовые схемы И и одна четырехвходовая схема ИЛИ, У1скнф–четыре трехвходовые схемы ИЛИ и одна четырехвходовая схема И, У2сднф–шесть трехвходовых схем И и одна шестивходовая схема ИЛИ, У2скнф–две трехвходовые схемы ИЛИ и одна двухвходовая схема И.
Минимизация булевых функций. Основная задача состоит в получении такой формы, которой соответствует логическая функция с минимальным числом элементов. Различают несколько методов минимизации булевых функций. При эвристических методах преобразования логических функций, использующих законы алгебры логики. Конечный вид минимизируемой функции в значительной степени зависит от квалификации и опыта разработчика цифровых устройств. Методы Квайна и Мак-Класки используются, вследствие четко сформулированных правил проведения отдельных операций, для минимизации сложных функций по разработанным алгоритмам с использованием ЭВМ. Метод карт Карно или карт Вейча, отличающихся способом обозначения строк и столбцов таблицы истинности, нашел применение при минимизации логических функций с числом двоичных переменных не боле 5-6.
Метод карт Карно. Карту Карно можно рассматривать как графическое представление совокупности всех наборов переменных для данного числа переменных. Каждый набор переменных изображается на карте в виде клетки. Таким образом, при n=3 карта имеет 8 клеток, а при n=6 – 64 клетки, рис.1.7,1.8 соответственно.
Рис.1.7
Рис.1.8. Карта Карно образуется путем такого расположения клеток, при котором наборы переменных, находящиеся в соседних клетках, отличаются значением одной переменной. В картах Карно соседними считаются также крайние клетки каждого столбца или строки. Расположенные в них наборы переменных отличаются значением одной переменной. Минтермы логической функции, т.е. наборы двоичных переменных, при которых эта функция равна 1, отмечаются единицами в соответствующих клетках. Для наборов переменных не входящих в логическую функцию соответствующие им клетки остаются пустыми. Логическая функция, записанная в СДНФ или заданная в виде таблицы истинности, переносится на карту Карно. Затем карта покрывается контурами. В контур может входить 2n рядом расположенных клеток, содержащих единичное значение логической функции, т.е. 2,4,8 и т.д. точек. Допускается пересечение контуров. Два минтерма, находящиеся в соседних клетках, т.е. в одном контуре, могут быть заменены одним логическим произведением, содержащим на одну переменную меньше. Исключается та переменная, которая меняет своё значение при переходе из одной клетки в другую. Если соседними являются две пары минтермов, то такая группа из четырех минтермов может быть заменена конъюнкцией двоичных переменных, содержащих на две переменных меньше. В общем случае, наличие единиц в 2n соседних клетках позволяет исключить n переменных. При минимизации с помощью карт Карно рекомендуется следовать следующему правилу: Необходимо образовывать контура, в которые входило бы максимально возможное количество клеток с минтермами - произведение будет наиболее простым. Контуров должно быть как можно меньше, чтобы было меньше слагаемых. После покрытия карты контурами производится их анализ с точки зрения уменьшения числа переменных. На основе анализа контуров записывается минимизированная ДНФ (МДНФ) логической функции в виде логической суммы логических произведений двоичных переменных. При этом двоичные переменные, имеющие единичное значение записываются без инверсии, а имеющие нулевое значение с инверсией. Минимизацию с помощью карт Карно можно использовать и для логических функций представленных в СКНФ. В этом случае, наборы двоичных переменных, при которых логическая функция равна 0 (макстермы), отмечаются нулями в соответствующих клетках карты. Аналогично образуются контура, охватывающие клетки с макстермами, далее контура анализируются, и записывается минимальная КНФ (МКНФ) логической функции в виде логического произведения логических сумм двоичных переменных, в которых двоичные переменные, имеющие нулевое значение, записываются без инверсии, а имеющие единичное значение с инверсией. В качестве примера минимизации с помощью карт Карно взяты логические функции, приведенные в табл.1.3. Карта Карно для функции У1 приведена на рис.1.9.
Карта Карно для функции у2 приведена на рис.1.10.
Рис.1.10. Карта Карно для функции у2
Карты Карно для функций у1 и у2 приведены на рис 9 и 10, соответственно. После минимизации с помощью карт Карно получаются следующие минимальные дизъюнктивная и конъюнктивная нормальные формы логических функций у1 и у2:
у2мднф=х1+х2+х3 , у2мкнф=х1+х2+х3.
При реализации логических функций на элементах Шеффера (И-НЕ) необходимо дважды проинвертировать МДНФ функций у1 и у2:
Схемы реализации функций у1 и у2 на элементах Шеффера приведены на рис.1.11 и 1.12.
Рис.1.11
Рис.1.12
Часть 1. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 ;
; 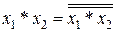 ;
; 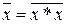




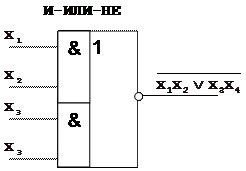





 у2
у2







 Рис.1.9. Карта Карно для функции У1
Рис.1.9. Карта Карно для функции У1
 ,
, ,
, ,
, 

