|
|
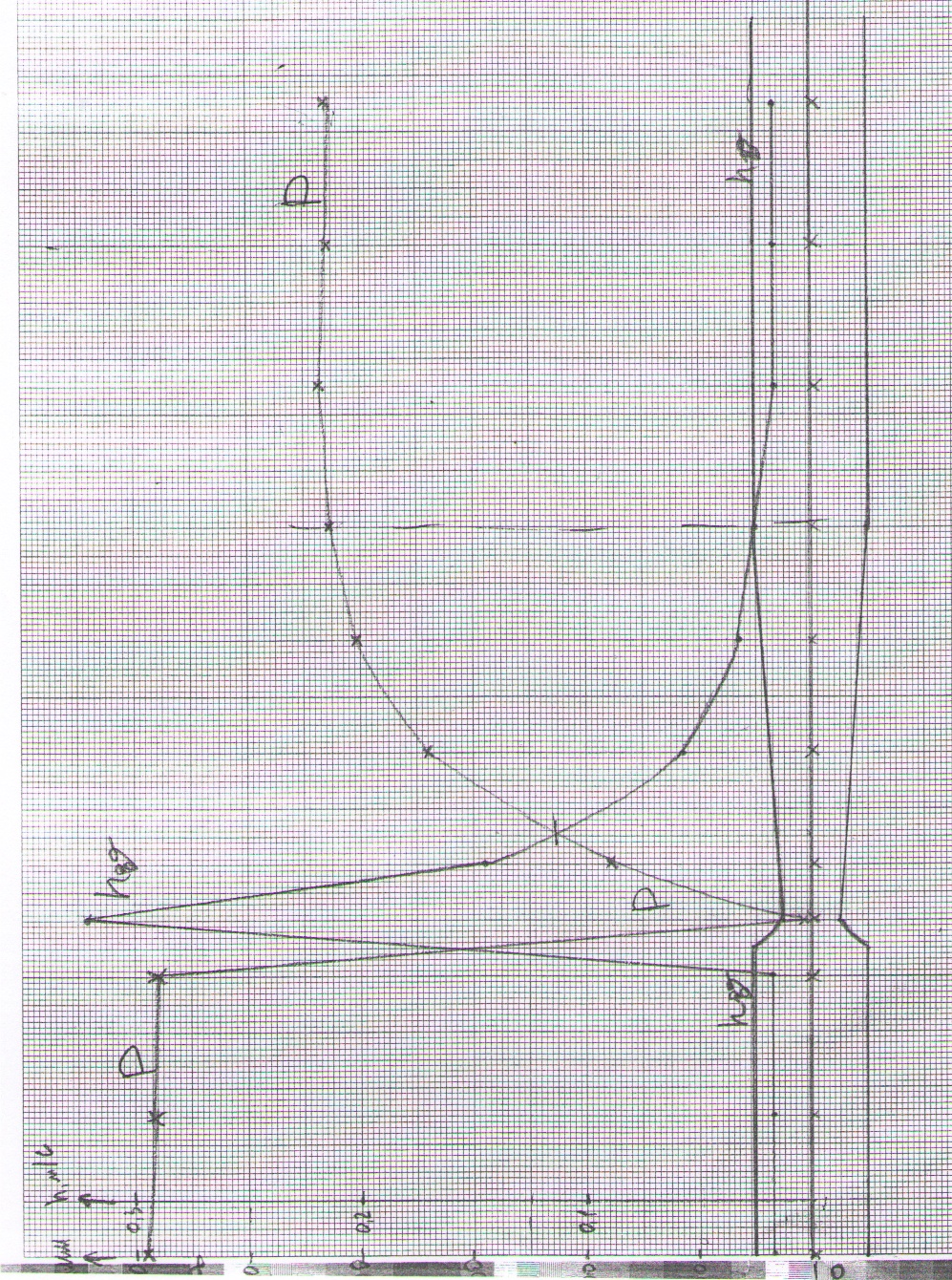
Обработка опытных данных.По результатам измерений следует вычислить скорость в каждом i-том сечении испытываемой трубы, включая и участок трубы Вентури υ1= На миллиметровую бумагу нанести: - профиль трубы Вентури в выбранном масштабе; - откладывая от оси трубы пьезометрические напоры для каждого i-того сечения вычертить пьезометрическую линию (или линию удельной потенциальной энергии): - аналогично вычертить линию скоростного напора (или линию удельной кинетической энергии); - суммируя скоростные напоры с ординатами пьезометрической линии в соответствующих сечениях, провести линию полного напора (или линию полной удельной энергии): - провести напорную плоскость (горизонтальную прямую) па уровне ординаты линии энергии первого пьезометра и обозначить потери напора (энергии) между этим сечением и любым, расположенным ниже по течению. Графики и профиль трубы с линиями (пьезометрической, скоростного напора и удельной энергии) в выбранном масштабе сделать на всю площадь стандартного листа миллиметровой бумаги (пример см. на рис. 17). В отчете по работе студентам рекомендуется дать объяснения получившейся конфигурации энергетических графиков.
Рис. 17. Профиль модуля М3 с участком трубы Вентури и экспериментальными линиями (пьезометрические, скоростного напора и удельной энергии). Контрольные вопросы. 1. Напишите уравнение Бернулли в напорах для идеальной и реальной жидкости. 2. Дайте определения пьезометрическому, скоростному и полному напорам. 3. Раскройте физический смысл этих напоров. 4. Как записывается уравнение Бернулли в давлениях и энергиях? 5. В чем причина энергетических потерь при истечении жидкости в трубопроводах? 6. Как рассчитывается диаметр в каждом сечении трубы Вентури? Привести пример. 7. Какие преобразования энергии текущей жидкости происходят в трубе Вентури? 8. Как вычерчиваются диаграммы Бернулли? 9. Сколько диаграмм надо нарисовать для каждого режима течения? 10. Чего следует добиваться при проектировании трубопроводов для снижения энергетических потерь? 11. Какие меры предпринимаются при строительстве трубопроводов для снижения энергетических потерь?
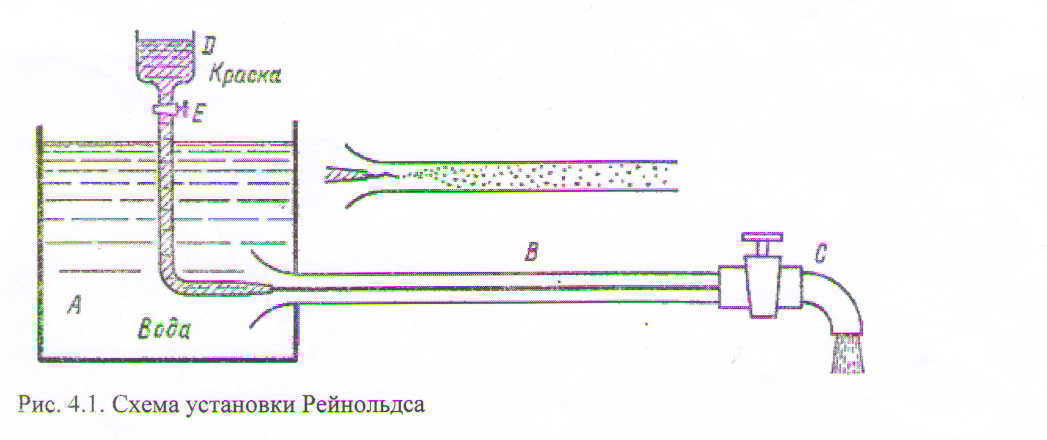
Лабораторная работа № 9 НАБЛЮДЕНИЕ РЕЖИМОВ ТЕЧЕНИЯ И ОПРЕДЕЛЕНИЕ ПАРАМЕТРОВ ПОТОКА. Цель работы: экспериментальная иллюстрация существования двух режимов течения жидкости – ламинарного и турбулентного; определение основных параметров одномерного потока жидкости и критического значения числа Рейнольдса. Основные задачи: измерение температуры жидкости; определение коэффициента кинематической вязкости жидкости (по справочным таблицам); определение расхода жидкости методом мерной кружки; расчет площади сечения трубы, средней скорости потока и числа Рейнольдса Краткая теория. Ламинарным называется слоистое течение без перемешивания частиц жидкости и без пульсации скорости и давления. Турбулентным называется течение, сопровождающееся интенсивным перемешиванием жидкости с пульсацией скорости и давления. Наряду с основным продольным перемещением жидкости наблюдаются поперечные перемещения и вращательные движения частиц жидкости. Переход от ламинарного режима к турбулентному наблюдается при определенной скорости движения жидкости. Эта скорость называется критической Vкр.. Значение этой скорости прямо пропорционально кинематической вязкости жидкости и обратно пропорционально диаметру трубы:
Рис. 18. Установка Рейнольдса для наблюдения режимов течения. Входящий в эту формулу безразмерный коэффициент, одинаков для всех жидкостей и газов и любых диаметров труб и называется критическим числом Рейнольдса. Для труб круглого сечения Re примерно равно 2300. Меньше этого числа течение – ламинарное, а больше – турбулентное. Однако имеет место переходная, критическая область от 2300 до 4000. При значениях больше 4000 устанавливается вполне развитое турбулентное течение. Режим движения жидкости напрямую влияет на гидравлическое сопротивление трубопроводов. Формула потерь напора в трубе постоянного диаметра записывается так: hпот = 32 vlVср./gd2 , или после преобразований принимает вид универсальной формулы Дарси-Вейсбаха: hпот = λ * l * V2/2 gd , где λ – коэффициент гидравлического трения, который для ламинарного течения вычисляется по выражению λ = 64/ Re ( по мнению некоторых авторов, например Т.М.Башта λ = 75/ Re). В режиме турбулентном вид формулы такой же, но расчет гидравлического коэффициента трения будет производиться по разным формулам в зависимости от скорости течения (или от числа Re) и от относительной шероховатости внутренней поверхности трубы ε = ∆/R, где ∆ - абсолютная шероховатость трубы, R – гидравлический радиус трубы. Для круглых труб R = d, тогда относительная шероховатость ε = ∆/ d. Иногда применяют обратную величину относительной шероховатости и называют ее относительной гладкостью 1/ε = d /∆. T AgAAEwAAAAAAAAAAAAAAAAAAAAAAW0NvbnRlbnRfVHlwZXNdLnhtbFBLAQItABQABgAIAAAAIQA4 /SH/1gAAAJQBAAALAAAAAAAAAAAAAAAAADsBAABfcmVscy8ucmVsc1BLAQItABQABgAIAAAAIQBS 0yokDwIAACgEAAAOAAAAAAAAAAAAAAAAADoCAABkcnMvZTJvRG9jLnhtbFBLAQItABQABgAIAAAA IQCqJg6+vAAAACEBAAAZAAAAAAAAAAAAAAAAAHUEAABkcnMvX3JlbHMvZTJvRG9jLnhtbC5yZWxz UEsBAi0AFAAGAAgAAAAhAEwGsr3hAAAACgEAAA8AAAAAAAAAAAAAAAAAaAUAAGRycy9kb3ducmV2 LnhtbFBLAQItAAoAAAAAAAAAIQDGMH69JwgMACcIDAAUAAAAAAAAAAAAAAAAAHYGAABkcnMvbWVk aWEvaW1hZ2UxLnBuZ1BLBQYAAAAABgAGAHwBAADPDgwAAAA= ">
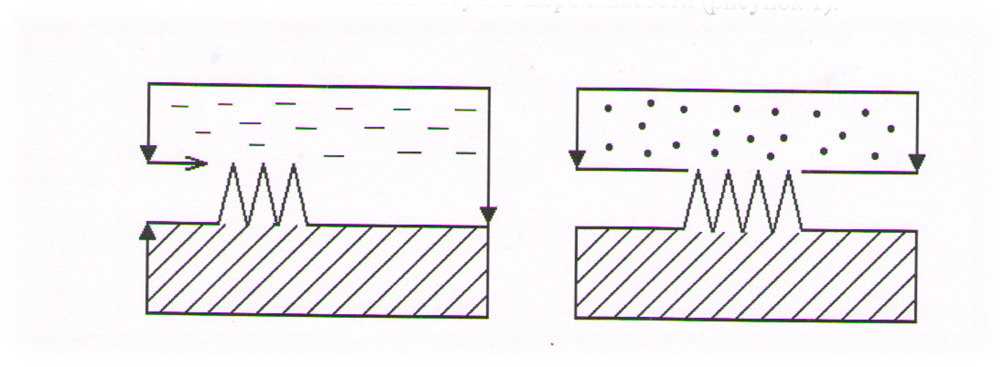
Рис. 19. Образование ламинарной пленки в гидравлически гладких трубах. Экспериментально установлено, что при турбулентном режиме на стенках трубы образуется тонкий слой жидкости с ламинарным режимом течения – ламинарная пленка, толщина которой может быть больше или меньше выступов шероховатости (рис. 19). Если выступы шероховатости тонут в ламинарной пленке (dпл. > ∆), то при таком режиме трубы гидравлически гладкие. Когда при больших числах Рейнольдса ламинарная пленка разрушается она покрывает выступы шероховатости, то трубы шероховатые (dпл. < ∆). 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 , а затем скоростной напор
, а затем скоростной напор 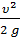
 Vкр = v * k/d, где v – кинематическая вязкость жидкости; k – безразмерный коэффициент; d – внутренний диаметр трубы.
Vкр = v * k/d, где v – кинематическая вязкость жидкости; k – безразмерный коэффициент; d – внутренний диаметр трубы.