
|
|
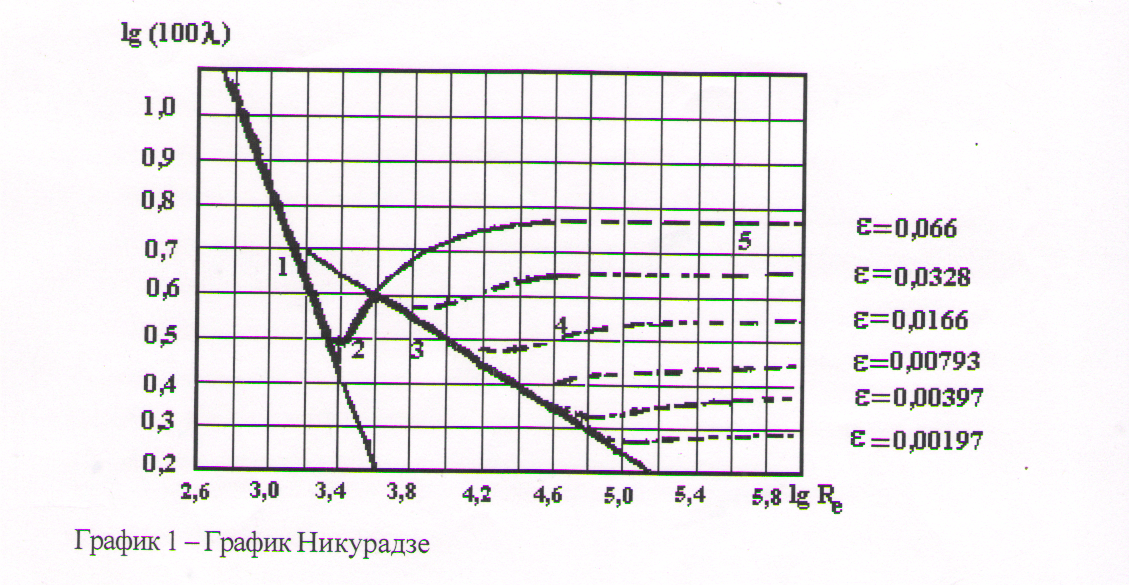
Обработка результатов опытов.По результатам измерений рассчитываются следующие величины: Потери напора по длине hпот = h1 - h2; - средняя скорость потока в трубе υ = 4Q/ π - гидравлический коэффициент трения из формулы: - численные значения измерений и вычислений свести в единую таблицу № 6 (см. Приложение), которую представить в отчете по лабораторной работе. По полученным данным построить участок графика зависимости гидравлического коэффициента трения от числа Рейнольдса в логарифмическом масштабе ( рис. 9) или график этой же зависимости в обычном масштабе ( рис. 10).
Рис. 9. График зависимости гидравлического коэффициента трения от числа Рейнольдса в логарифмическом масштабе (график Никурадзе).
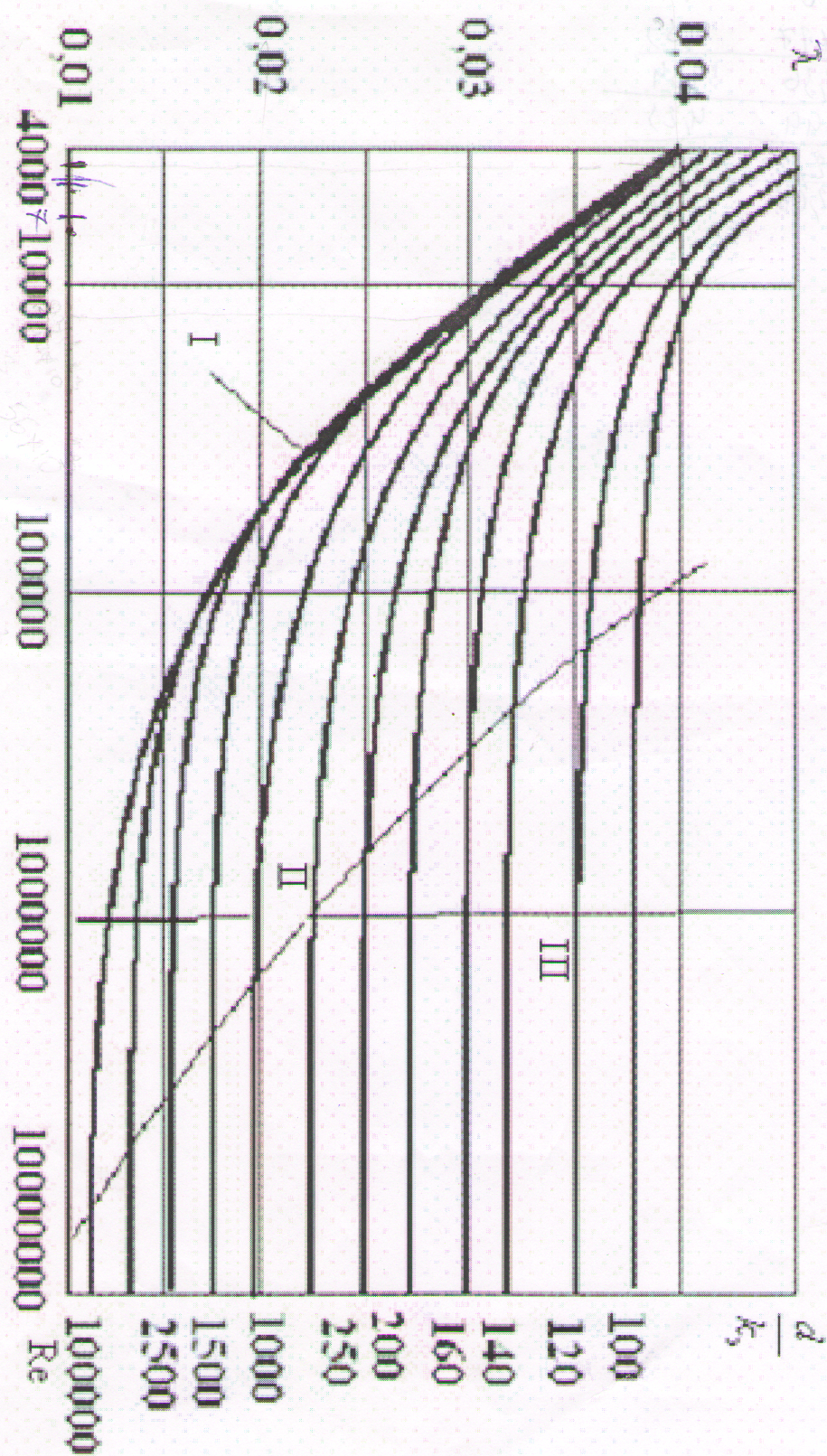
Рис. 10. График зависимости гидравлического коэффициента трения от числа Рейнольдса (график Мурина). На рис. 11 представлен аналогичный график Мурина только(рис. 10) и участок с равномерной шкалой гидравлических сопротивлений, в отличие от графика на рис. 10, где эта же зависимость представлена с неравномерной шкалой гидравлических сопротивлений. Для удобства наложения следует использовать график на рис. 11. Построенный участок кривой λ = λ (Re) следует наложить на известные из литературы графики Никурадзе или Мурина и сделать заключения: - о зоне гидравлического сопротивления, которой соответствуют проведенные опыты; - о величине относительной эквивалентной шероховатости испытываемой трубы. Графики выполнить на всю площадь стандартного листа миллиметровой бумаги в выбранном масштабе. Рис. 11.. Контрольные вопросы. 1. Какие виды гидравлических сопротивлений Вы знаете? 2. Приведите формулу потерь напора по длине в круглой трубе. 3. Как рассчитывается число Рейнольдса? 4. Что такое кинематическая вязкость, в каких единицах она измеряется? 5. Как зависит кинематическая вязкость от температуры жидкости? 6. Что такое эквивалентная относительная шероховатость? 7. Как определить расход жидкости по ротаметрам? Укажите единицы измерения расхода в системе СИ. 8. Укажите расчетную формулу для определения гидравлического коэффициента трения. 9. Что собой представляют пьезометрические линии? 10. Почему снятие показаний пъезометров следует производить только при установившемся режиме течения? 11. В чем основная сложность наложения экспериментальных графиков на известные из литературы? 12. Почему важно знать число Рейнольдса для определения зоны гидравлического сопротивления? Лабораторная работа № 7. ОПРЕДЕЛЕНИЕ ПОТЕРЬ НАПОРА НА ВНЕЗАПНОМ РАСШИРЕНИИ. Цель работы: определить потери напора на внезапном расширении при различных режимах течения жидкости (не менее 4), экспериментально изучить закономерности потерь напора и распределения давлений, скоростного напора, удельной энергии текущей жидкости в местных сопротивлениях. Основные задачи: - расчет средней скорости потока, гидравлического коэффициента местного сопротивления, числа Рейнольдса; - построить на миллиметровой бумаге в выбранном масштабе профиль трубы и начертить пьезометрические линии (не менее 4), линии скоростного напора и линии энергии текущей жидкости; - построить участок графика зависимости коэффициента местного сопротивления от числа Рейнольдса. Краткая теория. Основной формулой, связывающей величину потерь напора с параметрами потока и характерными размерами трубы, является формула 1.
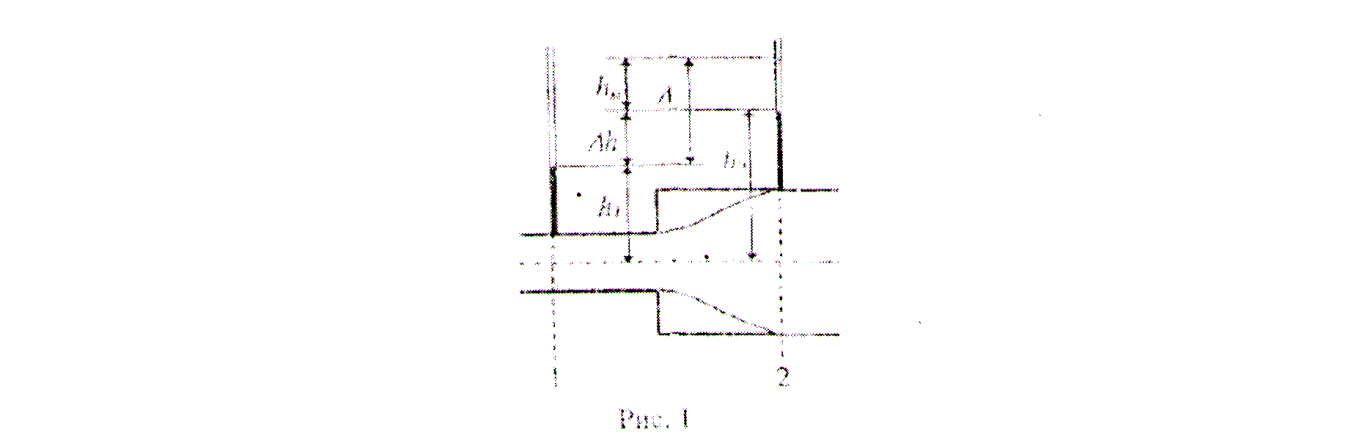
Рис. 12. Схема участка трубы с внезапным расширением. h пот = где υ1 и h пот =(1- S12/S22)2 * υ12/2g= ξ* υ12/2g где S1 и S2 – площади нормальных сечений; ξ – коэффициент потерь на внезапном расширении. Следует подчеркнуть, что данная формула получена из теоретической схемы, в которой игнорируются потери трения, а также предполагается равномерное распределение скоростей в сечениях труб. Поэтому коэффициент оказывается независимым от числа Рейнольдса, а сама формула отражает лишь так называемый квадратичный участок кривой, где в реальных условиях влияние числа Рейнольдса отсутствует. Существуют два подхода к экспериментальному определению коэффициента потерь на внезапном расширении. Первый состоит в его определении по измерениям давлений и скоростей в двух контрольных сечениях. При таком способе учитывается не только потери на внезапном расширении, но и потери трения на контрольном участке. Согласно другому подходу, из полного коэффициента исключаются потери на трение, что можно сделать с помощью построения линии энергии по длине участка расширения путем вычисления потерь на трение по формуле равномерного движения или по данным опытов на специально оборудованной установке. 2. Порядок выполнения работы. Работа выполняется на модуле М2 (рис.13). Для выполнения работы необходимо:
Рис. 13. Схема и размеры (в мм) модуля М2. - включить насос HI на панели управления; -установить необходимый расход с помощью вентилей В2, В1 в выходного вентиля модуля В4. Наблюдая за столбиками воды в пьезометрических трубках убедиться, что достигнут установившийся режим течения, и выполнить измерения: - расхода воды по ротаметрам; -показаний пьезометров. После занесения данных измерений в таблицу 7 (см. Приложение) изменить расход с помощью вентиля В4 и после достижения установившегося режима повторить все измерения. Для надежной серии опытов рекомендуется произвести их не менее чем для трех расходов и заполнить три такие таблицы, которые представить в отчете по лабораторной работе. 3.Обработка результатов опытов. При определении коэффициента местного сопротивления (в данном случае внезапного расширения) необходимо иметь в виду, что за местным сопротивлением, где поток претерпевает значительную деформацию лежит достаточно протяженный «участок стабилизации», на котором существует крупные вихри с возвратными течениями. Поэтому экспериментальный коэффициент местного сопротивления должен учитывать полные потери на участке стабилизации, а значит должен явно зависеть от числа Рейнольдса. Совпадение с теоретической формулой Борда можно ожидать только при весьма больших числах Рейнольдса. Расчетными соотношениями для определения коэффициента местного сопротивления по экспериментальным данным являются следующие. Применительно к рисунку 15, из уравнения Бернулли для сечения 1 и 2 получается hпот .=( где hпот. – искомые потери на внезапном расширении. Здесь сечение 2 выбирается на расстоянии достаточном для расширения потока на все сечение S2. Разделив потери к скоростному напору υ12/2g, получим:
2g * hпот/ υ12 = ξ = 1 – (S12/S22) –
Разности пьезометрических напоров скорость υ1no расходу, измеренному ротаметром. Тогда последняя формула позволяет вычислить экспериментальное значение ξ. Измерив пьезометрами давления во всех точках их подключения, следует построить пьезометрическую линию вдоль трубы, линию скоростного напора, а также линию энергии. Студентам рекомендуется объяснить физическую сущность этих графиков, а также обозначить на них потери напора в местном сопротивлении. Построить участок графика зависимости коэффициента местного сопротивления от числа Рейнольдса и, сравнивая полученную зависимость с графиком, выполненным на предыдущей работе, сделать вывод. Графики и профиль трубы с линиями (пьезометрической, скоростного напора и удельной энергии) в выбранном масштабе сделать на всю площадь стандартного листа миллиметровой бумаги (пример см. на рис. 14). Контрольные вопросы. 1. Что такое местные гидравлические сопротивления? Приведите примеры местных сопротивлений (не менее 5). 2. Приведите формулу расчета потерь напора на внезапном расширении. 3. По какой формуле вычисляется гидравлический коэффициент на внезапном расширении? 4. Укажите два подхода к экспериментальному определению коэффициента внезапного расширения. 5. Назовите основные участки кривой зависимости энергетических потерь от скорости течения (числа Рейнольдса). 6. Почему на внезапном расширении поток жидкости претерпевает деформацию? 7. Какими движениями частиц жидкости характеризуется достаточно протяженный «участок стабилизации» после внезапного расширения? 8. Лабораторная работа № 8 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 ;
; =
=  пот d/L
пот d/L  ;
;


 2- средние скорости в исследуемых сечениях. Используя уравнения неразрывности, эту формулу можно представить в виде
2- средние скорости в исследуемых сечениях. Используя уравнения неразрывности, эту формулу можно представить в виде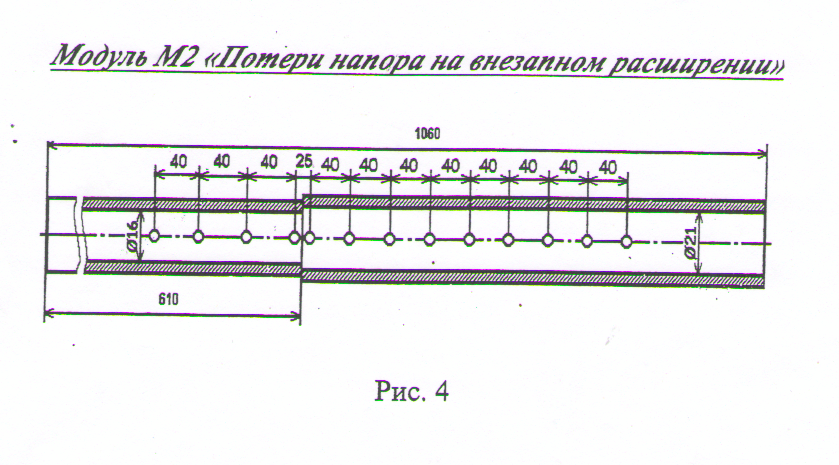
 /ρg + υ12/2g) – (
/ρg + υ12/2g) – (  /ρg + υ22/2g),
/ρg + υ22/2g), *2g/ υ12 .
*2g/ υ12 . Рис. 14. Профиль трубы и линии (пьезометрические, скоростного напора).
Рис. 14. Профиль трубы и линии (пьезометрические, скоростного напора).