
|
|
Прямолинейное равноускоренное движение сосуда с жидкостью.Равномерное вращение сосуда с жидкостью.Уравнение поверхности равного давления.-Жидкость покоится в сосуде, неподвижном относительно земли, а также в сосуде, движущемся равномерно и прямолинейно.
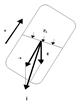
Рис. 2.10 Пусть сосуд с жидкостью движется прямолинейно с постоянным ускорением а. В этом случае результирующую массовую силу, действующую на жидкость, найдем как сумму векторов силы инерции, направленной в сторону, обратную ускорению а, и силы тяжести (рис. 2.10). Обозначив вектор равнодействующей силы, отнесенной к единице массы, через j, получим j = a +g; где a и g – векторы единичных сил инерции и тяжести. Для всех частиц рассматриваемого объема жидкости равнодействующие массовые силы параллельны друг другу, а поверхности уровня перпендикулярны этим силам, поэтому все поверхности уровня, в том числе и свободная поверхность, являются плоскостями, параллельными друг другу. Угол наклона этих плоскостей к горизонту определяется из условия перпендикулярности их к силе j. Для полного решения о положении свободной поверхности жидкости в сосуде, движущемся прямолинейно равноускоренно, необходимо к предыдущему условию добавить уравнение объемов, т. е. нужно знать объем жидкости в сосуде, выразить его через размеры сосуда и первоначальный уровень жидкости.Давление в любой точке рассматриваемого объема жидкости может быть получено аналогично тому, как это определялось при выводе основного уравнения гидростатики . -Возьмем открытый цилиндрический сосуд с жидкостью и сообщим ему постоянную угловую скорость w вращения вокруг вертикальной оси. Жидкость постепенно приобретет ту же угловую скорость, что и сосуд, а свободная поверхность ее видоизменится: в центральной части уровень жидкости понизится, у стенок – повысится, и вся свободная поверхность жидкости станет некоторой поверхностью вращения . На жидкость в этом случае будут действовать две массовые силы, сила тяжести и центробежная сила, которые, будучи отнесенными к единице массы, соответственно равны g и w2r. Равнодействующая массовая сила j увеличивается с увеличением радиуса за счет второй составляющей, а угол наклона ее к горизонту уменьшается. Эта сила нормальна к свободной поверхности жидкости, поэтому угол наклона поверхности к горизонту возрастает с увеличением радиуса. Найдем уравнение положения свободной поверхности.
Учитывая, что сила j нормальна к свободной поверхности, получим
В точке пересечения свободной поверхности с осью вращения C = h, поэтому окончательно будем иметь
После интегрирования
-Поверхность, во всех точках которой значения гидростатического давления равны между собой, называют поверхностью равного давления или поверхностью уровня. На положение уровня свободной поверхности влияют силы тяжести и инерции. Найдем величину равного давления Р по трем частным производным. При Р=const и р # 0 значение полного дифференциала dP=0 и, следовательно, уравнение поверхности жидкости равного давления имеет вид : 8. Виды движения жидкости. Траектории жидких частиц. Линия тока, трубка тока, элементарная струйка. Живое сечение потока. Установившееся движение жидкости – это движение жидкости, параметры которого не зависят от времени, а зависят от координат. Неустановившееся движение – параметры зависят и от координат, и от времени. Равномерное – параметры потока жидкости не меняются по длине и по времени. Напорное – движение жидкости в потоке без свободной поверхности. Одномерное – параметры зависят только от одной координаты. Двухмерное (плоский поток) – параметры зависят от двух координат. Вихревое – частицы жидкости совершают вращение. Потенциальное (безвихревое) – не совершается вращательное движение. Траектория – это путь одной и той же частицы за определенный промежуток времени. Линия тока – это линия, в каждой точке которой в данное мгновение вектор скорости частицы совпадает с направлением касательной к этой линии. При установившемся режиме линия тока и траектория совпадают. Трубка тока – это поверхность, образованная линиями тока пересекающие замкнутый контур в выделенной жидкости. Часть потока внутри трубки тока называется элементарной струйкой. Свойства элементарной струйки. 1. Эл.струйка является мгновенно существующей при неустановившемся режиме, а для установившегося режима это поток бесконечно малых размеров. 2. Через боковые поверхности элементарной струйки жидкость не вытекает. Живое сечение – это такое сечение, в каждой точке которого вектор скорости ему перпендикулярен. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
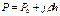 В частном случае, когда а = 0 и соответственно j = g, формула (2.9) превращается в основное уравнение гидростатики
В частном случае, когда а = 0 и соответственно j = g, формула (2.9) превращается в основное уравнение гидростатики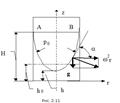
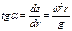 получаем после интрегрирования
получаем после интрегрирования 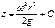
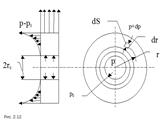
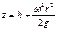 т. е. свободная поверхность жидкости является параболоидом вращения. Максимальную высоту подъема жидкости можно определить исходя из равенства объемов неподвижной жидкости и жидкости во время вращения.На практике очень часто приходится иметь дело с вращением сосуда, заполненного жидкостью, вокруг горизонтальной оси. При этом угловая скорость w столь велика, что сила тяжести на порядок меньше центробежных сил, и ее действие можно не учитывать. Закон изменения давления в жидкости для этого случая получим из рассмотрения уравнения равновесия элементарного объема с площадью основания dS и высотой dr, взятой вдоль радиуса (рис. 2.12). На выделенный элемент жидкости действуют силы давления и центробежная сила.Обозначив давление в центре площадки dS, расположенной на радиусе r, через p, а в центре другого основания объема (на радиусе r + dr) через p + dp, получим следующее уравнение равновесия выделенного объема в направлении радиуса:
т. е. свободная поверхность жидкости является параболоидом вращения. Максимальную высоту подъема жидкости можно определить исходя из равенства объемов неподвижной жидкости и жидкости во время вращения.На практике очень часто приходится иметь дело с вращением сосуда, заполненного жидкостью, вокруг горизонтальной оси. При этом угловая скорость w столь велика, что сила тяжести на порядок меньше центробежных сил, и ее действие можно не учитывать. Закон изменения давления в жидкости для этого случая получим из рассмотрения уравнения равновесия элементарного объема с площадью основания dS и высотой dr, взятой вдоль радиуса (рис. 2.12). На выделенный элемент жидкости действуют силы давления и центробежная сила.Обозначив давление в центре площадки dS, расположенной на радиусе r, через p, а в центре другого основания объема (на радиусе r + dr) через p + dp, получим следующее уравнение равновесия выделенного объема в направлении радиуса: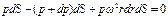 или
или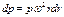
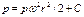 Постоянную C найдем из условия, что при r = r0 p = p0.Следовательно
Постоянную C найдем из условия, что при r = r0 p = p0.Следовательно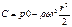 Подставив ее значение в предыдущее уравнение, получим связь между p и r в следующем виде:
Подставив ее значение в предыдущее уравнение, получим связь между p и r в следующем виде: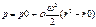 Очевидно, что поверхностями уровня в данном случае будут цилиндрические поверхности с общей осью – осью вращения жидкости.
Очевидно, что поверхностями уровня в данном случае будут цилиндрические поверхности с общей осью – осью вращения жидкости.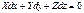 Это уравнение называется уравнением поверхности жидкости равного или постоянного давления.
Это уравнение называется уравнением поверхности жидкости равного или постоянного давления.