
|
|
Вопрос 10. Уравнение Прандтля для пограничного слоя.Рассмотрим ламинарный пограничный слой на теле малой кривизны.
Запишем уравнение Навье-Стокса для установившегося плоского движения вязкой жидкости будут иметь вид:
Т.к. движение плоское, то действием массовых сил можно пренебречь. Уравнение неразрывности:
Граничные условия: 1. граничное условие прилипания: при y=0 Vx=Vy=0; 2. при y=δ Vx=U(x) – на внешней границе пограничного слоя. Ввиду малости толщины пограничного слоя в этих уравнениях можно отбросить численно малые члены. Для этого проанализируем порядок величин, входящих в уравнение. Примем, что порядок Из уравнения неразрывности:
Запишем уравнения Навье-Стокса через порядок величин.
Очевидно, что порядок длины много больше порядка толщины ПС: Анализ первого уравнения. Для того чтобы силы вязкости в первом уравнении не получились равными нулю, порядок слагаемого
И последнего уравнения найдем порядок δ.
Таким образом, относительная толщина ПС будет тем меньше, чем больше число Re. Проанализируем порядок слагаемых второго уравнения.
Сравним порядок слагаемых первого и второго уравнения. Получаем, что порядок слагаемых второго уравнения пренебрежимо мал по сравнению с порядком слагаемых первого уравнения. Следовательно, во тором уравнении остается только одна величина: Это означает, что давление, которое направлено по нормали к поверхности будет одинаково на границе ПС и на поверхности тела на одной нормали. Также это означает, что давление является функцией координаты x – P(x). Поле распределения давления на границе пограничного слоя можно получить решая уравнения динамики идеальной жидкости, т.е. уравнения внешнего потока. Таким образом, уравнения Навье-Стокса после отбрасывания бесконечно малых членов будут иметь вид:
Уравнение 4.1 – уравнение Прандтля для ламинарного пограничного слоя. В уравнениях Прандтля для установившегося течения в двумерном ламинарном ПС, дополненных уравнением неразрывности 3 неизвестных: Vx, Vy, p. Второе уравнение Прандтля говорит о том, что Таким образом,
где p – избыточное давление; V=U(x) – скорость на границе ПС. Продифференцировав, это уравнение получим:
Тогда 1-ле уравнение Прандтля с учетом
В этом случае есть два уравнения с двумя неизвестными: Vx и Vy. Таким образом, из уравнений Прандтля можно найти касательные напряжения и силу сопротивления трения.
Аналогичные уравнения могут быть записаны и для турбулентного ПС. В этом случае, используются осредненные значения скоростей и давлений. Если в качестве исходных данных принять уравнения Рейнольдса и произвести оценку роли отдельных слагаемых для потока внутри ПС можно получить два упрощенных уравнения в проекциях на оси x и y, дополненные уравнением нерарывности, записанном с учетом осредненных скоростей.
или:
- система уравнений для турбулентного ПС. где Решение уравнений для ламинарного и турбулентного ПС свяано со значительными трудностями. Для решения этих уравнений необходимы следующие граничные условия: 1. прилипания Vx=Vy=0 при 2. U(x)=U при При определении закона распределения (эпюры) скорости в пограничном слое (в турбулентном это будут осредненные скорости). Для турбулентного ПС вводят дополнительные гипотезы, которые позволяют выразить турбулентные касательные напряжения через осредненные скорости или характеристики турбулентного потока. Более простыми способами являются методы расчета плоского ПС, основанные на применении интегральных соотношений. Решение уравнений Прандтля представляется сложной математической задачей. Точные решения, могут быть получены для ламинарного ПС пластины, поскольку давление по всей длине пластины не меняется. В этом случае Решение плоской задачи при плоском безградиентном течении в ПС производится введением функции тока ψ. Введением функции тока и записью проекций скоростей через нее 1. 2. Интегрирование полученного после преобразований единственного нелинейного дифференциального уравнения осуществлялось численными методами Блазиусом, а впоследствии более точно и другими учеными. Касательные напряжения получены в виде:
Толщина ПС 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|



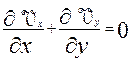
 ,
,  ,
, 

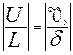
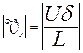

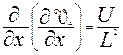

 .
. должен быть равен порядку слагаемых в левой части первого уравнения, следовательно, порядок
должен быть равен порядку слагаемых в левой части первого уравнения, следовательно, порядок 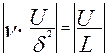 . Отсюда найдем порядок кинематического коэффициента вязкости.
. Отсюда найдем порядок кинематического коэффициента вязкости.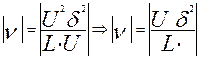
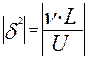



 - изменение давления по толщине ПС.
- изменение давления по толщине ПС.
 . Таким образом, равенство давления во всех точках одной нормали к поверхности тела может рассматриваться как интеграл второго уравнения Навье-Стокса. Однако, в этом случае давление как функция x не определяется и рассчитывается во внешнем потоке.
. Таким образом, равенство давления во всех точках одной нормали к поверхности тела может рассматриваться как интеграл второго уравнения Навье-Стокса. Однако, в этом случае давление как функция x не определяется и рассчитывается во внешнем потоке. входящее в первое уравнение Прандтля будет связано со скоростью потока на внешней границе ПС интегралом Эйлера:
входящее в первое уравнение Прандтля будет связано со скоростью потока на внешней границе ПС интегралом Эйлера: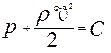
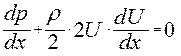 (
(  )
) 
 примет вид:
примет вид:


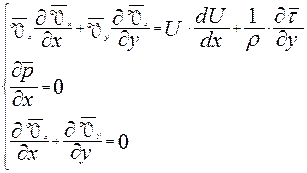
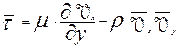
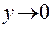 ;
;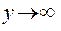 .
.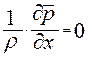 . Такие течения называют безградиентными, поскольку градиент давления отсутствует.
. Такие течения называют безградиентными, поскольку градиент давления отсутствует.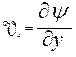 ;
; 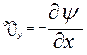 уменьшается и число неизвестных, а также упрощаются и граничные условия:
уменьшается и число неизвестных, а также упрощаются и граничные условия: при y=0;
при y=0; при
при  . Введя местный коэффициент трения
. Введя местный коэффициент трения 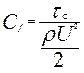 установили его зависимость от числа Рейнольдса:
установили его зависимость от числа Рейнольдса:  - коэффициент зависящий от координаты x.
- коэффициент зависящий от координаты x.
 - коэффициент трения общий для всей пластины.
- коэффициент трения общий для всей пластины.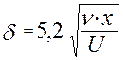 т.е. растет вниз и уменьшается с ростом скорости. Решение уравнений Прандтля должно подчиняться граничным условиям на границе ПС, следовательно для решения уравнений необходимо заранее знать эту границу. Задача об определении границы ПС является сложной, поскольку эпюра скорости асимптотически подходит к вертикальной линии. Наклон эпюры и определяет трудность решения задачи. Для упрощения задачи были разработаны специальные методы, получившие название интегральное соотношение для ПС.
т.е. растет вниз и уменьшается с ростом скорости. Решение уравнений Прандтля должно подчиняться граничным условиям на границе ПС, следовательно для решения уравнений необходимо заранее знать эту границу. Задача об определении границы ПС является сложной, поскольку эпюра скорости асимптотически подходит к вертикальной линии. Наклон эпюры и определяет трудность решения задачи. Для упрощения задачи были разработаны специальные методы, получившие название интегральное соотношение для ПС.