
|
|
Уравнение Бернулли для элементарной струйки и потока реальной жидкостиУравнение Бернулли выражает закон сохранения энергии, связывающий удельную по весу энергию жидкости в двух сечениях потока.
Здесь: Если ввести обозначения:
H1 = H2 + h1-2 Потери напора, отнесенные к единице длины струйки, называются гидравлическим уклоном, и обычно обозначаются буквой i; таким образом
19.Геометрический и энергетический смысл уравнения Бернулли. Все члены уравнения Бернулли выражаются в единицах длины, поэтому каждый из них может называться высотой: z — геометрическая высота, или высота положения; p/γ— пьезометрическая высота или высота гидродинамического давления; v2/(2g) — высота, соответствующая скоростному напору; hпот.-высота, соответствующая потерям напора. Следовательно, геометрический смысл уравнения Бернулли может быть сформулирован так: при установившемся движении жидкости сумма четырех высот (высоты положения, пьезометрической высоты, высоты, соответствующей скоростному напору, и высоты, соответствующей потерям напора) остается неизменной вдоль потока. Кроме того, каждый из членов уравнения Бернулли выражает удельную энергию потока, т. е. энергию, приходящуюся на единицу веса движущейся жидкости: z — удельная энергия положения; p/γ— удельная энергия гидродинамического давления; v2/(2g)—удельная кинетическая энергия; hпот — потери удельной энергии. Энергетический смысл уравнения Бернулли можно сформулировать следующим образом: при установившемся движении жидкости сумма четырех удельных энергий (энергии положения, энергии гидродинамического давления, кинетической энергии и потерь энергии) остается неизменной вдоль потока. Если в каком-либо сечении потока жидкости (рис. 15) установить две трубки — пьезометрическую 1 и скоростную 2, нижний изогнутый конец которой направлен против течения, то в скоростной трубке создается дополнительное давление от воздействия скорости движущейся жидкости. Высота подъема жидкости в скоростной трубке больше высоты подъема жидкости в пьезометрической трубке на скоростной напор v2/(2g). Все члены уравнения Бернулли представлены графически на рис. 16. Здесь в четырех выбранных сечениях потока SS установлены пьезометрические и скоростные трубки. Если соединить уровни жидкости в пьезометрах, то получим пьезометрическую линию, или линию потенциальной удельной энергии. Она находится на расстоянии z + p/γ от плоскости сравнения 0-0.
Падение этой линии на единицу длины называется пьезометричеческим уклоном J. Соединяя уровни жидкости в скоростных трубках, получим напорную линию или линию, суммарной (потенциальной и кинетической) удельной энергии. Падение напорной линии на единицу длины называется гидравлическим уклоном i и характеризует потери напора на единицу длины. 20. Как уже упоминалось, коэффициент носит название коэффициента кинетической энергии, корректива скорости, коэффициента Кориолиса. Выясним физический смысл этой величины. Как уже отмечалось выше, второй член в уравнении (9.13) представляет собой кинетическую энергию секундной массы потока, определяемую истинным распределением скоростей в сечении, т.е. (9.23) Если бы скорости в сечении были бы распределены равномерно, то ( - средняя скорость потока), и кинетическая энергия потока была бы (9.24) Разделив (9.23) на (9.24), получим: (9.25) Следовательно, коэффициент Кориолиса представляет собой отношение кинетической энергии потока, вычисленной по истинному распределению скоростей, к кинетической энергии, определенной по средней скорости. Для уяснения вопроса рассмотрим гипотетический «поток», состоящий из двух струек, скорости которых м/с и м/с и вычислим коэффициент Кориолиса. Истинная кинетическая энергия (сумма кинетических энергий струек) Средняя скорость ; и , т. е. (истинная кинетическая энергия больше средней). Легко убедится, что чем больше неравномерность распределения скоростей, тем больше коэффициент Кориолиса. Так, если м/с, а м/с, то . Очевидно, что минимальное значение будет при равномерном распределении скоростей. Действительно, пусть м/с, тогда и . Следовательно, можно утверждать, что корректирует ошибку, возникающую при вычислении кинетической энергии при замене истинного распределения скоростей условным равномерным. Забегая несколько вперед, отметим, что в природе существует два принципиально отличающихся режима течения жидкости: ламинарный и турбулентный. При ламинарном течении в трубах , при турбулентном . Это позволяет утверждать, что в турбулентном потоке скорости в поперечном сечении распределены существенно равномерней, чем в ламинарном (эпюра турбулентного потока более «наполненная», ближе к прямоугольной по сравнению с эпюрой ламинарного потока).
Изменение энергии по длине потока удобно проследить на графиках. Из уравнения Бернулли для потока реальной жидкости (закона сохранения энергии) видно, что гидродинамическая линия для потока реальной жидкости (с одним источником энергии) всегда ниспадающая. То же справедливо и для пьезометрической линии, но только в случае равномерного движения, когда скоростной напор Пьезометрическим уклоном называют изменение удельной потенциальной энергии жидкости вдоль потока, приходящееся на единицу его длины.
Если гидравлический уклон всегда положителен, то пьезометрический может быть и положительным, и отрицательным. При равномерном движении жидкости, когда скорость по длине потока не изменяется, скоростной напор вдоль потока av2/ (2g) = const. Следовательно, пьезометрическая линия параллельна энергетической, и пьезометрический уклон равен гидравлическому. Изменение удельной потенциальной энергии положения вдоль потока жидкости, приходящееся на единицу длины, называют геометрическим уклоном iи определяют по формуле
где l — расстояние между сечениями потока. Сформулируем два условия применимости к потоку жидкости уравнения Бернулли: 1) движение жидкости должно быть установившимся; 2) движение жидкости в сечениях 1—2, 2—2 и 3—3,cоединяемых уравнением Бернулли, должно быть параллельно струйным или плавноизменяющимся, в промежутке же между сечениями 1—1, 2—2 и 3—3 движение жидкости может быть и резко меняющимся. Напорная линия (см. рис. 12) графически изображает напоры вдоль потока. Отметки этой линии могут быть определены с помощью трубок Питó или расчётом. По ходу движения она всегда падает с уклоном, так как потери напора не обратимы. Пьезометрическая линия (линия давлений) графически отражает напоры вдоль потока без скоростного напора hV , поэтому она располагается всегда ниже напорной линии. Отметки этой линии могут быть зарегистрированы непосредственно пьезометрами или, с пересчётом, манометрами. В отличие от напорной линии, пьезометрическая — может понижаться или повышаться вдоль потока (рис. 13).
21.3 Режимы движения жидкости
Силы вязкости в жидкости существенно влияют на величину и распределение скоростей движения жидкости, т.е. на характер ее движения. Различают два режима движения: ламинарный и турбулентный. При ламинарном режиме жидкость движется отдельными слоями, пульсаций скоростей и давлений не наблюдается. Турбулентный режим характеризуется неупорядоченным, хаотичным движением частиц и интенсивным перемешиванием жидкости. Критерием для определения режима движения является безразмерное число Рейнольдса. Для труб круглого сечения число Рейнольдса определяется по формуле
где V – средняя скорость жидкости;
Экспериментально определено, что режим будет ламинарным, если
Ламинарный режим возникает в тонких капиллярных трубках, во время движения очень вязких жидкостей, при фильтрации воды в слоях грунта и др. Движение маловязких жидкостей (вода, бензин, спирт) почти всегда происходит в турбулентном режиме. Число, или, правильнее, критерий Рейно́льдса ( Число Рейнольдса определяется следующим соотношением:
где · · · · · · · Для каждого вида течения существует критическое число Рейнольдса, Значения Re выше критического и до определённого предела относятся к переходному (смешанному) режиму течения жидкости, когда турбулентное течение более вероятно, но ламинарное иногда тоже наблюдается — то есть, неустойчивая турбулентность. Числу Reкр 2300 соответствует интервал 2300-10 000; для упомянутого примера с тонкими плёнками это 20-120 — 1600. Число Рейнольдса как критерий перехода от ламинарного к турбулентному режиму течения и обратно относительно хорошо действует для напорных потоков. При переходе к безнапорным потокам переходная зона между ламинарным и турбулентным режимами возрастает, и использование числа Рейнольдса как критерия не всегда правомерно. Например, вводохранилищах формально вычисленные значения числа Рейнольдса очень велики, хотя там наблюдается ламинарное течение. Напротив, возмущения потока могут значительно снижать величину . . Стоит отметить, что для газов Reкр достигается при значительно бо́льших скоростях, чем у жидкостей, поскольку у первых куда больше кинематическая вязкость (в 10-15 раз). Критерий назван в честь выдающегося английского физика О. Рейнольдса (1842—1912), автора многочисленных пионерских работ по гидродинамике.
22. Наблюдения за величинами осреднённых скоростей в турбулентном потоке жидкости показали, что эпюра осреднённых скоростей в турбулентном потоке в значительной степени сглажена и практически скорости в разных точках живого сечения равны средней скорости.
Сопоставляя эпюры скоростей турбулентного потока (эпюра 1) и ламинарного потока позволяют сделать вывод о практически равномерном распределении скоростей в живом сечении. Работами Прандтля было установлено, что закон изменения касательных напряжений по сечению потока близок к логарифмическому закону. При некоторых допущениях: течение вдоль бесконечной плоскости и равенстве касательных напряжений во всех точках на поверхности
После интегрирования: Последнее выражение преобразуется к следующему виду:
Развивая теорию Прандтля, Никурадзе и Рейхардт предложили аналогичную зависимость для круглых труб. 23.Ламина́рное тече́ние (лат. lāmina — «пластинка») — течение, при котором жидкость или газ перемещается слоями без перемешивания и пульсаций (то есть беспорядочных быстрых изменений скорости и давления). До 1917 года в российской науке пользовались термином Струйчатое течение. Только в ламинарном режиме возможно получение точных решений уравнения движения жидкости (уравнений Навье — Стокса), например течение Пуазейля. [править]Переход к турбулентности Ламинарное течение возможно только до некоторого критического значения числа Рейнольдса, после которого оно переходит в турбулентное. Критическое значение числа Рейнольдса зависит от конкретного вида течения (течение в круглой трубе, обтекание шара и т. п.). Например, для течения в круглой трубе
Схематичное изображение ламинарного (a) и турбулентного (b) течения в плоском слое В некоторых случаях для получения порогового числа Рейнольдса достаточно провести линейный анализ устойчивости — теоретический анализустойчивости под воздействием бесконечно малых возмущений. Так, например, получены пороги для течения между параллельными плоскостями и течения Тейлора между вращающимися цилиндрами. Однако в некоторых случаях линейного анализа недостаточно: для течения в круглой трубе он приводит к абсолютной устойчивости, что опровергается экспериментами. В гидравлике, если труба некруглого сечения, то Reкр рассчитывается по гидравлическому диаметру dг=4F/χ, где F — площадь поперечного сечения трубы, χ — полный смоченный периметр. Теоретические и экспериментальные исследования показывают, что потери напора на трение по длине вычисляются по формуле Дарси-Вейсбаха
где l- расстояние между рассматриваемыми сечениями, т.е. длина трубы, v - скорость течения, d- внутренний диаметр трубы, Для ламинарного режима движения жидкости
24.
Экспериментальное изучение коэффициента Дарси λ от числа Re и относительной шероховатости для шероховатых труб было проведено И. Никурадзе а для прямоугольных лотков с искусственной (песочной) шероховатостью (открытые потоки) – А.П. Зегждой. (Рис. 3.13). Для создания этой равнозернистой шероховатости через сита просеивали песок одной фракции, т.е. одинаковых размеров. Затем равномерно наносили песок на стенки, покрытые лаком. Песок приклеивался к стенкам. Размеры зерен песка принимали за размер выступа шероховатости Δ.В результате для опытов были подготовлены трубы и лотки с различными значениями относительной шероховатости стенок: Δ / ro или Δ / d для труб и Δ / R для лотков или относительной гладкости: ro /Δ, d / Δ и R /Δ. В опытах были измерены потери напора hc по показателям пьезометрических высот по длине и расход Q, вычислены средние скорости потоков и коэффициенты гидравлического трения λ.По существу исследователями делалась попытка оценить влияние как внутреннего трения, так и поверхностного трения, а также турбулентного перемешивания в пристенном пограничном слое труб и лотков на основные гидравлические характеристики потоков вязкой жидкости. При некотором значении Re (тем меньшего, чем больше относительная шероховатость) коэффициент Дарси λперестает зависеть от числа Re. Проявляется автомодельность режима. При турбулентном режиме движения потока вязкой жидкости при одних и тех же значениях Re коэффициентλтем больше, чем выше относительная шероховатость труб (или каналов). Результаты своих исследований И. Никурадзе представил в виде графика λ =f (Re; Δ/ ro) (рис. 3.12). Они наглядно свидетельствуют о наличии различных областей гидравлического сопротивления при напорном движении потока вязкой жидкости в трубах. 25. Потери напора в местных сопротивлениях. Как уже указывалось, местные потери напора возникают вследствие изменения скорости по величине и направлению и зависят в основном от геометрических размеров и форм местных сопротивлений, определяемых через коэффициент местного сопротивления ζ. Обычно коэффициент местного сопротивления ζ определяют экспериментальным путем и выражают в виде эмпирических формул, графиков или в табличной форме. Лишь для некоторых местных сопротивлений получены теоретические зависимости (см. Справочник по гидравлическим сопротивлениям, И.Е. Идельчик). К наиболее распространённым местным сопротивлениям относятся: внезапное расширение потока (рис. 21), внезапное сужение потока (рис. 22), диафрагма (рис. 23), диффузор (рис. 24) и конфузор (рис. 25).
Формула Вейсбаха[1] в гидравлике — эмпирическая формула, определяющая потери напора или потери давления при развитом турбулентном течении несжимаемой жидкости нагидравлических сопротивлениях (предложена Юлиусом Вейсбахом (англ.) в 1855 году):
где · · · · · величина Формула Вейсбаха, определяющая потери давления на гидравлических сопротивлениях, имеет вид:
где
26. К местным сопротивлениям в трубопроводах относятся различного рода фасонные части и арматура (сужения, расширения, повороты, краны, вентили, тройники и т.д.), необходимость установки которых вызывается условиями сооружения и эксплуатации трубопровода. Местные сопротивления вызывают изменение скорости движения жидкости либо по величине (сужения и расширения, рис.1), либо по направлению (колена, рис.2), либо то и другое одновременно (тройники).
Рис. 1
В зависимости от факторов, вызывающих потери напора, в местных сопротивлениях различают потери трения и потери в водоворотных областях (областях циркуляционного течения). Потери на трение вызываются торможением потока стенками, которое приводит к неравномерному распределению скоростей по сечениям потока и к появлению напряжений трения между смещающимися струйками жидкости. Местные деформации потока сопровождаются увеличением неравномерности скоростей в его сечениях, вызывающих возрастание местных потерь трения. Потери в областях циркуляционного трения связаны с отрывами потока от стенок, происходящими при резких изменениях конфигурации каналов. Возникающее в этих местах интенсивное циркуляционное движение приводит к сильному возрастанию местной потери напора. В таких сопротивлениях, как внезапное расширение, колено, диафрагма, задвижка и др. основными являются потери в водоворотных областях, а тормозящее действие стенок на поток играет второстепенную роль. При движении жидкости в изогнутых каналах (см.рис.2) возникает неравномерность скоростей в сечениях потока, которая увеличивает потери трения и может приводить к отрывам потока от стенки. При этом основным источником значительных потерь в этих отводах является водоворотная область у внутренней стенки.
Рис. 2
На преодоление местных сопротивлений тратится некоторая часть энергии (напора) потока, которая является местной потерей энергии (напора). При практических расчетах ее принято определять в долях удельной кинетической энергии (скоростного напора) по формуле Вейсбаха
где z – коэффициент местного сопротивления (безразмерный), величина которого в основном зависит от вида местного сопротивления;
В тех случаях, когда скорость потока перед местным сопротивлением и после него будет различна (например внезапное сужение или расширение), потеря напора может выражаться через скоростной напор
Здесь u1 – средняя скорость движения жидкости в сечении потока перед местным сопротивлением; u2 – то же, за местным сопротивлением. На практике для расчетов обычно принимают скорость потока за местными сопротивлениями. Для случая внезапного расширения русла коэффициент сопротивления можно рассчитать по формуле, полученной на основе теоремы об изменении количества движения
где s1 – площадь поперечного сечения потока до расширения; s2 – то же, после расширения. Для внезапного сужения русла коэффициент сопротивления можно рассчитать по полуэмпирической формуле
где s1 – площадь поперечного сечения потока до сужения; s2 – то же, после сужения; Коэффициент местного сопротивления запорных устройств в основном зависит от формы и степени их открытия. 27. 28. Определение потерь напора по длине. Потери напора по длине трубопровода обычно определяют по формуле Дарси-Вейсбаха. При этом необходимо устанавливать значения коэффициента гидравлического трения λ, что составляет одну из сложнейших проблем механики жидкости, не получившую до сих пор полного теоретического решения. Коэффициент λ зависит от числа Рейнольдса и относительной шероховатости труб. В зависимости от шероховатости можно выделить три области их работы: область гидравлически гладких труб (малые числа Рейнольдса), область шероховатого трения (большие числа Рейнольдса), переходная область между ними. В области гидравлически гладких труб коэффициент λ зависит только от числа Рейнольдса. В переходной области коэффициент λ зависит от числа Рейнольдса и относительной шероховатости. В области квадратичного сопротивления коэффициент λ зависит только от относительной шероховатости. Для определения коэффициента гидравлического трения λ, при турбулентном режиме предложен ряд обобщенных формул, действительных в широком диапазоне чисел Рейнольдса и относительной шероховатости. Например, широкое распространение имеет формула Кольбрука:
Для области гидравлически гладких труб она преобразуется в формулу Прандтля:
Для области квадратичного сопротивления в формула Никурадзе:
При практических расчётах значения эквивалентной шероховатости принимают с учётом материала стенок труб и их состояния, зависящего от продолжительности эксплуатации. Расчет водопроводных сетей из стальных и чугунных труб, бывших в эксплуатации, обычно проводят по формулам Ф. А. Шевелева (см. Таблицы гидравлического расчёта водопроводных труб, Справочное пособие, Ф.А. Шевелёв, А.Ф. Шевелёв). 29.Местными гидравлическими сопротивлениями называются любые участки гидравлической системы, где имеются повороты, преграды на пути потока рабочей жидкости, расширения или сужения, вызывающие внезапное изменение формы потока, скорости или направления ее движения. В этих местах интенсивно теряется напор. Примерами местных сопротивлений могут быть искривления оси трубопровода, изменения проходных сечений любых гидравлических аппаратов, стыки трубопроводов и т.п. Потери напора на местных сопротивлениях
где Коэффициент местного сопротивления зависит от конкретных геометрических размеров местного сопротивления и его формы. В связи со сложностью процессов, которые происходят при движении жидкости через местные сопротивления, в большинстве случаев его приходится определять на основании экспериментальных данных. Однако в некоторых случаях величины коэффициентов местных сопротивлений можно определить аналитически. Из определения коэффициента Коэффициенты различных сопротивлений можно найти в гидравлических справочниках. В том случае, если местные сопротивления находятся на расстоянии меньше (25ч50)d друг от друга ( 30.Истечение жидкости из малого отверстия в тонкой стенке при постоянном напоре. Отверстие считают малым, если его размер по высоте значительно меньше высоты столба жидкости Н над ним - не более 0,1Н. Тонкой стенкой считают такую, у которой отверстие имеет заостренную кромку; при этом струя, вытекающая из отверстия, преодолевает лишь местные сопротивления. Рассмотрим сосуд, имеющий в вертикальной стенке отверстие площадью w, через которое вытекает жидкость под постоянным напором Н (рис. 26). При вытекании струи жидкости из отверстия на некотором расстоянии от него наблюдается сжатие ее поперечного сечения. Отношение площади сжатого сечения wс к площади отверстия w называют коэффициентом сжатия: e = wс / w
При истечении жидкости из отверстия задача сводится к определению скорости истечения и расхода жидкости. Подобные практические задачи решаются с помощью составления уравнения Бернулли для двух сечений, одно из которых сжатое, а другое произвольное. Расчётная формула для определения расхода жидкости через малое отверстие в тонкой стенке имеет вид:
где m - коэффициент расхода отверстия. На основе многочисленных опытов установлено, что значение коэффициента m при полном совершенном сжатии колеблется в пределах 0,59-0,63. Истечение жидкости из малого отверстия в тонкой стенке при переменном напоре представляет собой один из примеров неустановившегося движения жидкости. Ниже приведены схемы (рис. 27 и рис. 28) для двух простейших случаев, иллюстрирующих истечение жидкости из отверстия при переменном напоре.

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
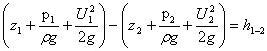
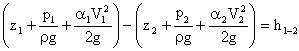
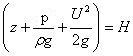
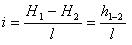
 , отнесенная к единице длины струйки, называется пьезометрическим уклоном j.
, отнесенная к единице длины струйки, называется пьезометрическим уклоном j.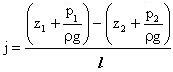
 Рис.15. Схема установки
пьезометрической
и скоростной трубок
Рис.15. Схема установки
пьезометрической
и скоростной трубок
 Рис. 16. Графическое изображение членов
уравнения Бернулли
Рис. 16. Графическое изображение членов
уравнения Бернулли
 .
. а уменьшение напора происходит только за счёт изменения потенциальной энергии потока, главным образом за счёт уменьшения давления P.
а уменьшение напора происходит только за счёт изменения потенциальной энергии потока, главным образом за счёт уменьшения давления P.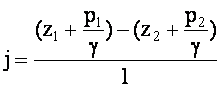
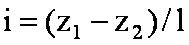

 , (3.4)
, (3.4) - диаметр трубы;
- диаметр трубы; - кинематический коэффициент вязкости жидкости.
- кинематический коэффициент вязкости жидкости.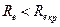 .
. - критическое число Рейнольдса, при котором происходит переход ламинарного режима в турбулентный. Для круглых труб принимают
- критическое число Рейнольдса, при котором происходит переход ламинарного режима в турбулентный. Для круглых труб принимают  . Если число Рейнольдса находится в области
. Если число Рейнольдса находится в области  , то режим считается переходным, а при
, то режим считается переходным, а при  - турбулентным.
- турбулентным.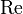 ), — безразмерная величина, характеризующая отношение нелинейного и диссипативного членов в уравнении Навье — Стокса[1]. Число Рейнольдса также считается критерием подобия течения вязкой жидкости.
), — безразмерная величина, характеризующая отношение нелинейного и диссипативного членов в уравнении Навье — Стокса[1]. Число Рейнольдса также считается критерием подобия течения вязкой жидкости.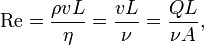
 — плотность среды, кг/м3;
— плотность среды, кг/м3; — характерная скорость, м/с;
— характерная скорость, м/с; — характерный размер, м;
— характерный размер, м; — динамическая вязкость среды, Н·с/м2;
— динамическая вязкость среды, Н·с/м2; — кинематическая вязкость среды, м2/с(
— кинематическая вязкость среды, м2/с(  ) ;
) ; — объёмная скорость потока;
— объёмная скорость потока; — площадь сечения трубы.
— площадь сечения трубы. течение происходит в ламинарном режиме, при
течение происходит в ламинарном режиме, при  возможно возникновение турбулентности. Критическое значение числа Рейнольдса зависит от конкретного вида течения (течение в круглой трубе, обтекание шара и т. п.), различными возмущениями потока, как-то изменение направленности и модуля вектора скорости потока, шероховатость стенок, близость местных сопротивлений и др. Например, для течения (точнее, для стабилизированного изотермического потока) жидкости в прямой круглой[источник не указан 376 дней]трубе с очень гладкими стенками
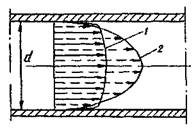
возможно возникновение турбулентности. Критическое значение числа Рейнольдса зависит от конкретного вида течения (течение в круглой трубе, обтекание шара и т. п.), различными возмущениями потока, как-то изменение направленности и модуля вектора скорости потока, шероховатость стенок, близость местных сопротивлений и др. Например, для течения (точнее, для стабилизированного изотермического потока) жидкости в прямой круглой[источник не указан 376 дней]трубе с очень гладкими стенками  . Для движения плёнки жидкости с относительно гладкой поверхностью раздела с газом при двухфазном потоке
. Для движения плёнки жидкости с относительно гладкой поверхностью раздела с газом при двухфазном потоке  .
.
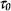
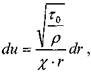
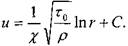
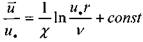
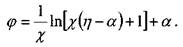
 .
.

 ,
, - коэффициент гидравлических потерь на трение по длине,
- коэффициент гидравлических потерь на трение по длине,  - относительная шероховатость.
- относительная шероховатость. .
. (1.87)
Итак, различают стенки (трубы, русла) гидравлически гладкие и шероховатые. Такое разделение является условным, поскольку, как следует из формулы (1.87), толщина ламинарной пленки обратно пропорциональна числу Рейнольдса (или средней скорости). Таким образом, при движении вдоль одной и той же поверхности с неизменной высотой выступа шероховатости в зависимости от средней скорости (числа Рейнольдса) толщина ламинарной пленки может изменяться. При увеличении числа Рейнольдса толщина ламинарной пленки δуменьшается и стенка, бывшая гидравлически гладкой, может стать шероховатой, так как высота выступов шероховатости окажется больше толщины ламинарной пленки и шероховатость станет влиять на характер движения и, следовательно, на потери напора.
Для последующих практических расчетов можно принимать ориентировочные значения высоты выступа шероховатости для труб: трубы новые стальные и чугунные - Δ ≈ 0,45 - 0,50 мм, трубы, бывшие в эксплуатации (так называемые «нормальные»), Δ ≈ 1,35 мм.
Таким образом, зная высоту выступа шероховатости и определив толщину ламинарной пленки, можно, сравнив их размеры, определить, гидравлически гладкой или гидравлически шероховатой будет стенка, ограничивающая поток в трубе.
(1.87)
Итак, различают стенки (трубы, русла) гидравлически гладкие и шероховатые. Такое разделение является условным, поскольку, как следует из формулы (1.87), толщина ламинарной пленки обратно пропорциональна числу Рейнольдса (или средней скорости). Таким образом, при движении вдоль одной и той же поверхности с неизменной высотой выступа шероховатости в зависимости от средней скорости (числа Рейнольдса) толщина ламинарной пленки может изменяться. При увеличении числа Рейнольдса толщина ламинарной пленки δуменьшается и стенка, бывшая гидравлически гладкой, может стать шероховатой, так как высота выступов шероховатости окажется больше толщины ламинарной пленки и шероховатость станет влиять на характер движения и, следовательно, на потери напора.
Для последующих практических расчетов можно принимать ориентировочные значения высоты выступа шероховатости для труб: трубы новые стальные и чугунные - Δ ≈ 0,45 - 0,50 мм, трубы, бывшие в эксплуатации (так называемые «нормальные»), Δ ≈ 1,35 мм.
Таким образом, зная высоту выступа шероховатости и определив толщину ламинарной пленки, можно, сравнив их размеры, определить, гидравлически гладкой или гидравлически шероховатой будет стенка, ограничивающая поток в трубе.
 Рис. 21. Схема внезапного расширения потока
Рис. 21. Схема внезапного расширения потока
 Рис. 22. Схема внезапного сужения потока
Рис. 22. Схема внезапного сужения потока
 Рис. 23. Схема влияния диафрагмы на поток
Рис. 23. Схема влияния диафрагмы на поток
 Рис. 24. Схема потока в диффузоре
Рис. 24. Схема потока в диффузоре
 Рис. 25. Схема потока в конфузоре
Рис. 25. Схема потока в конфузоре
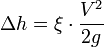
 — потери напора на гидравлическом сопротивлении;
— потери напора на гидравлическом сопротивлении; — коэффициент потерь (коэффициент Дарси);
— коэффициент потерь (коэффициент Дарси); — средняя скорость течения жидкости;
— средняя скорость течения жидкости; — ускорение свободного падения;
— ускорение свободного падения; называется скоростным (или динамическим) напором.
называется скоростным (или динамическим) напором.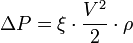
 — потери давления на гидравлическом сопротивлении;
— потери давления на гидравлическом сопротивлении;
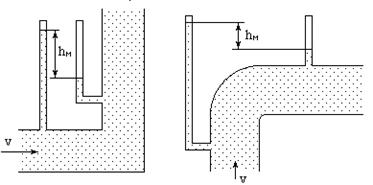
 (1)
(1) – кинетическая энергия (скоростной напор).
– кинетическая энергия (скоростной напор).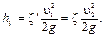
 (2)
(2) (3)
(3) степень сужения.
степень сужения.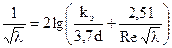
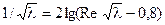
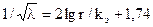
 определяются по формуле Вейсбаха:
определяются по формуле Вейсбаха: ;
; - коэффициент местного сопротивления.
- коэффициент местного сопротивления. видно, что он учитывает все виды потерь энергии потока жидкости на участке местного сопротивления. Его физический смысл состоит в том, что он показывает долю скоростного напора, затрачиваемого на преодоление данного сопротивления.
видно, что он учитывает все виды потерь энергии потока жидкости на участке местного сопротивления. Его физический смысл состоит в том, что он показывает долю скоростного напора, затрачиваемого на преодоление данного сопротивления. - диаметр трубопровода, соединяющего местные сопротивления), весьма вероятно их взаимное влияние друг на друга, а их действительные коэффициенты местных сопротивлений будут отличаться от табличных. Такие сопротивления нужно рассматривать как единое сложное сопротивление, коэффициент
- диаметр трубопровода, соединяющего местные сопротивления), весьма вероятно их взаимное влияние друг на друга, а их действительные коэффициенты местных сопротивлений будут отличаться от табличных. Такие сопротивления нужно рассматривать как единое сложное сопротивление, коэффициент  которого определяется только экспериментально. Нужно отметить, что из-за взаимного влияния местных сопротивлений, расположенных вблизи друг друга в потоке, во многих случаях суммарная потеря напора не равна простой сумме потерь напора на каждом из этих сопротивлений.
которого определяется только экспериментально. Нужно отметить, что из-за взаимного влияния местных сопротивлений, расположенных вблизи друг друга в потоке, во многих случаях суммарная потеря напора не равна простой сумме потерь напора на каждом из этих сопротивлений. Рис. 26. Схема свободного истечения жидкости из малого отверстия
в тонкой стенке
Рис. 26. Схема свободного истечения жидкости из малого отверстия
в тонкой стенке
 ,
,