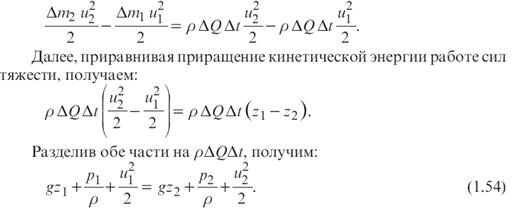|
|
Сила давления жидкости на криволинейные цилиндрические поверхности
Сила давления жидкости на криволинейную цилиндрическую поверхность (рис.2.10) складывается из горизонтальной
Горизонтальная составляющая
где Вертикальная составляющая
Объем тела давления - объем, заключенный между данной стенкой, свободной поверхностью жидкости и вертикальными плоскостями, проходящими по контуру стенки. 14.Установившееся и неустановившееся движение.Установившимся называют такое движение жидкости, при котором скорость потока и давление в любой его точке не изменяются с течением времени и зависят только от ее положения в потоке, т. е. являются функциями ее координат. Примерами установившегося движения могут служить истечение жидкости из отверстия резервуара при постоянном напоре, а также поток воды в канале при неизменном его сечении и постоянной глубине. Неустановившимся называют такое движение жидкости, при котором скорость движения и давление в каждой данной точке изменяются с течением времени.. Примером неустановившегося движения служит истечение жидкости из отверстия резервуара при переменном напоре. В этом случае в каждой точке сечения струи, вытекающей из отверстия, скорость движения и давление изменяются во времени.
Поток. Совокупность элементарных струек, представляющая собой непрерывную массу частиц, движущихся по какому-либо направлению, образует поток жидкости. Поток может быть полностью или частично ограничен твердыми стенками, например, в трубопроводе или канале, и может быть свободным, например, в виде струи, выходящей из сопла гидромонитора. Гидравлические элементы потока. К ним относят: живое сечение, расход, смоченный периметр, гидравлический радиус и среднюю скорость. Живым сечением ω потока называют поперечное сечение потока, перпендикулярное его направлению. Расходом потока Q называют объем жидкости, проходящей в единицу времени через живое сечение потока. Расход жидкости измеряют в м3/с или в л/с. Смоченным периметром χ называет часть периметра живого сечения, на которой жидкость соприкасается с твердыми стенками. Гидравлическим радиусом R называют отношение площади живого сечения потока к смоченному периметру: R = ω / χ . Гидравлический радиус измеряют в единицах длины. Средней скоростью потока v и называют частное от деления расхода потока на площадь его живого сечения: v = Q / ω Равномерное движение жидкости. Равномерным называют такое установившееся движение жидкости, при котором живые сечения и средняя скорость потока не меняются по его длине. Примером равномерного движения служит движение жидкости в цилиндрической трубе или в канале неизменного сечения и постоянной глубины. Неравномерным называют такое установившееся движение жидкости, при котором живые сечения и средние скорости потока изменяются по его длине. Примером неравномерного движения служит движение жидкости в конической трубе, в естественном русле, на перепаде. При равномерном движении линии тока представляют собой систему прямых параллельных линий (рис. 13). Такое движение называется также параллельноструйным. При движении жидкости в естественных руслах живое сечение обычно непрерывно изменяется вдоль потока как по форме, так и по площади, и движение жидкости является установившимся неравномерным.
Последнее свойство просто обосновывается. Если внутри плавно изменяющегося потока выделить частицу жидкости и спроектировать все действующие на нее силы на плоскость живого сечения, то вследствие того, что скорости и ускорения почти перпендикулярны живому сечению, силы инерции в уравнение равновесия не войдут; в связи с этим уравнение равновесия и закон распределения давления в плоскости живого сечения не будут отличаться от закона распределения давления в жидкости, находящейся в покое. Существуют понятия напорного и безнапорного потока. Напорным называется поток, у которого по всему периметру живого сечения жидкость соприкасается с твердыми стенками. Примером напорного потока может служить движение воды в водопроводных трубах. Безнапорным называется поток со свободной поверхностью. Примером безнапорного потока служит движение воды в реках, каналах, водоотводящих и водосточных трубах
15.Элементарная струйка. Если в движущейся жидкости выделить бесконечно малый замкнутый контур и через все его точки провести линии тока, соответствующие данному моменту времени, получится как бы трубчатая непроницаемая поверхность, называемая трубкой тока. Масса жидкости, движущейся внутри трубки тока, образует элементарную струйку. Элементарные струйки жидкости при установившемся движении обладают следующими свойствами: · площадь поперечного сечения струйки и ее форма с течением времени не изменяются, так как не изменяются формы линий токов; · перетекание жидкости через боковую поверхность элементарной струйки не происходит; · во всех точках поперечного сечения элементарной струйки скорости движения одинаковы вследствие малости площади поперечного сечения. Форма, площадь поперечного сечения элементарной струйки и скорости в различных поперечных сечениях струйки могут изменяться. Существуют понятия напорного и безнапорного потока. Напорным называется поток, у которого по всему периметру живого сечения жидкость соприкасается с твердыми стенками. Примером напорного потока может служить движение воды в водопроводных трубах. Безнапорным называется поток со свободной поверхностью. Примером безнапорного потока служит движение воды в реках, каналах, водоотводящих и водосточных трубах 16.Уравнение неразрывности потока. Рассмотрим установившееся движение жидкости в жестком русле переменного сечения (рис. 14).
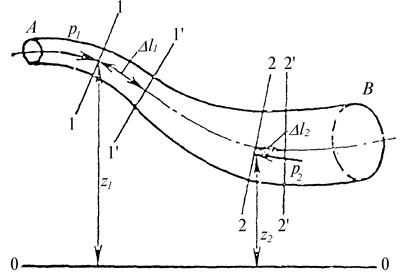
Масса m1 не может быть и меньше массы m2, так как разрыв в сплошном потоке при установившемся движении невозможен. Следовательно, m1 = m2 = const. Массы жидкости можно выразить в виде объемов, прошедших через сечения I—I и II—II за время Δt: m1 = ρ1Q1 Δt и m2 = ρ2Q2 Δt Так как m1 = m2 и ρ1 = ρ2 (жидкость несжимаема), то Q1= Q2 = const Это уравнение называют уравнением постоянства расхода. Из него следует, что при установившемся движении несжимаемой жидкости расход ее в любом сечении потока постоянен. Так как Q = vω, то уравнение может быть записано в следующем виде: v1ω1 = v2ω2 = const Данное уравнение называют уравнением неразрывности потока. Оно показывает, что при установившемся движении несжимаемой жидкости произведение площади живого сечения на среднюю скорость потока является постоянной величиной или, что средние скорости потока обратно пропорциональны площадям соответствующих живых сечений. Уравнение Бернулли для потока жидкости. Общий вид уравнения Бернулли для потока жидкости можно записать в виде: z + p/γ + αv2/(2g) + hпот. = const Коэффициент αучитывает влияние неравномерности распределения скоростей по сечению на удельную кинетическую энергию потока, вычисленную по средней скорости. Коэффициент α называют коррективом кинетической энергии или коэффициентом Кориолиса. 17. Рассмотрим элементарную струйку идеальной жидкости при установившемся движении. Выделим сечениями 1-1и 2-2отсек этой струйки (рис. 1.24). Высотное положение центров тяжести живых сечений относительно произвольно расположенной плоскости сравнения 00 характеризуется ординатами z1и z2. Давления в центрах сечений p1 и p2,скорости u1 и u2соответственно.
Рис. 1.24. Элементарная струйка идеальной жидкости при установившемся режиме движения Условимся, что на отсек действуют только силы тяжести и силы гидродинамического давления (силы внутреннего трения отсутствуют, поскольку жидкость невязкая). За малый промежуток времени Δtчастицы жидкости из 1-1переместятся в 1’-1’на расстояние Δl1 = u1Δt,а частицы из 2-2 - 2’-2’на расстояние Δl2 = u2Δt. Применим теорему кинетической энергии. Согласно теореме приращение кинетической энергии отсека должно быть равно сумме работ всех сил, действующих на отсек, при указанном движении. Работу производят силы тяжести и силы давления, действующие по крайним живым сечениям струйки. Направление по нормали к боковым поверхностям струйки (к направлению движения) давления окружающей массы невязкой жидкости работы не производят.
Приращение кинетической энергии отсека за tравно разности кинетических энергий элементов 1-1’и2-2’, так как в пределах участка 1’-2при установившемся движении кинетическая энергия остается постоянной. Тогда
Это и есть уравнение Бернулли для элементарной струйки невязкой жидкости при установившемся движении под действием сил тяжести.

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
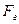 и вертикальной
и вертикальной  составляющих
составляющих . (2.17)
. (2.17)
 (2.18)
(2.18) - расстояние от свободной поверхности жидкости до центра тяжести ее вертикальной проекции;
- расстояние от свободной поверхности жидкости до центра тяжести ее вертикальной проекции;  -площадь вертикальной проекции.
-площадь вертикальной проекции. , т.е.
, т.е. . (2.19)
. (2.19) Рис.13. Схематическое изображение плавно изменяющегося движения
Рис.13. Схематическое изображение плавно изменяющегося движения
 Рис.14. Схема к выводу уравнения
неразрывности потока
Рис.14. Схема к выводу уравнения
неразрывности потока