
|
|
Основное уравнение гидростатикиГидростатическое давление и его свойства Гидростатика — раздел гидравлики, изучающий законы равновесия покоящейся жидкости. Жидкость, находящаяся в покое, подвергается действию внешних сил двух категорий: массовых и поверхностных. К массовым относятся силы, пропорциональные массе жидкости (сила тяжести, сила инерции). К поверхностным относятся силы, распределенные по поверхности, ограничивающей любой мысленно выделенный объем жидкости, и пропорциональные площади этой поверхности (сила давления, центробежная сила). Под действием внешних сил в каждой точке жидкости возникают внутренние силы, характеризующие ее напряженное состояние (давление в точке). Рассмотрим некоторый объем покоящейся жидкости (рис. 1). Мысленно разделим этот объем на две части произвольной плоскостью ABCD и отбросим верхнюю часть. Для сохранения равновесия нижней части к плоскости ABCD необходимо приложить силы, заменяющие действие верхней части объема жидкости на нижнюю.
В гидравлике силу
Иначе говоря, гидростатическое давление в точке является пределом отношения силы давления, действующей на элементарную площадку, к ее площади, если она стремится к нулю. Гидростатическое давление измеряется в единицах силы, деленных на единицу площади. В системе СИ за единицу давления принят паскаль (Па) — равномерно распределенное давление, при котором на площадь 1 м2 действует сила 1 Н. Гидростатическое давление обладает двумя свойствами: гидростатическое давление всегда направлено по внутренней нормали к площадке, на которую оно действует; гидростатическое давление в любой точке жидкости действует одинаково по всем направлениям, т. е. не зависит от угла наклона площадки, на которую оно действует. Причём гидростатическое давление всегда направлено по внутренней нормали.
Основное уравнение гидростатики
.Основное уравнение гидростатики. Закон Паскаля. Рассмотрим жидкость, находящуюся в покое, и определим гидростатическое давление р в точке А на бесконечно малой площадке dω, расположенной на глубине h от свободной поверхности жидкости и параллельной ей (рис. 2). Выделим над этой площадкой некоторый цилиндрический объем жидкости, заменив действие окружающей его среды силами давления на свободную поверхность p0dω , на нижнее основание цилиндра pdω и на его боковую поверхность.
Абсолютное, или полное, гидростатическое давление состоит из внешнего давления на свободную поверхность жидкости и манометрического (или избыточного) давления, которое создает слой воды над рассматриваемой точкой А (рис. 3).
Из рис. 3 следует, что в закрытом сосуде рабс = ратм + γhр, а с другой стороны рабс = р0 + γh, следовательно, ратм + γhр = р0 + γh или
hр = h + (р0 - ратм) / γ Величина hр — пьезометрическая высота, показывающая избыточное давление в точке, где присоединена трубка (пьезометр). В открытом сосуде hр = h, так как р0 = ратм, т. е, пьезометрическая высота будет равна глубине погружения точки А в жидкость. Высоту поднятия воды в пьезометре относительно плоскости отсчета 00 называют пьезометрическим напором Hр. Для закрытого сосуда: Hр = hр + z = h + z + (p0 - ратм) / γ Давление на жидкость ниже атмосферного называется вакуумом, т. е. вакуум — это недостаток давления до атмосферного: рвак = ратм - рабс Для измерения вакуума используют вакууметры (рис. 4).
Для измерения давления применяют пьезометры, жидкостные и механические манометры и вакуумметры. Пьезометр (см. рис. 3) представляет собой открытую сверху стеклянную трубку диаметром 5 — 12 мм, помещенную на измерительной шкале и соединенную нижним концом с той областью, где требуется измерить давление. Жидкость в пьезометре поднимается на высоту hр под действием давления р0 на свободной поверхности жидкости и веса столба жидкости высотой h. Избыточное гидростатическое давление в точке установки пьезометра составит ризб. = γhр, откуда hр = ризб. /γ Пьезометрическую высоту измеряют в метрах столба жидкости. Длина трубки пьезометра обычно не превышает 3—4 м. Жидкостные манометры отличаются от пьезометров тем, что в них используется жидкость с определенным удельным весом (вода, спирт, ртуть и др.). Простейшим является U-образный ртутный манометр, схема которого представлена на рис. 5. Высота трубки уменьшается по сравнению с трубкой обычного пьезометра в 13,6 раза, так как удельный вес ртути примерно в 13,6 раза больше удельного веса воды.
Вакуумметры (как и манометры) бывают жидкостными и механическими. Конструкция и принцип действия их аналогичны конструкции и принципу действия манометров 4. 5. Закон Паскаля формулируется так: Давление, производимое на покоящуюся жидкость или газ, передается в любую точку жидкости или газа одинаково по всем направлениям.Закон назван в честь французского учёного Блеза Паскаля.На основе закона Паскаля работают различные гидравлические устройства: тормозные системы, прессы и др.Данный закон является прямым следствием отсутствия сил трения покоя в жидкостях и газах.Закон Паскаля неприменим в случае движущейся жидкости (газа) — в этом случае необходимо пользоваться уравнениями гидродинамики, а также в случае, когда жидкость (газ) находится в гравитационном поле; так, известно, что атмосферное и гидростатическое давление уменьшается с высотой. Закон сообщающихся сосудов — один из законов гидростатики, гласящий, что в сообщающихся сосудах уровни однородных жидкостей, считая от наиболее близкой к поверхности земли точки, равны. Рассмотрим два сообщающихся сосуда, в которых находится жидкость плотностью 6. Плавание тел в жидкости. Закон Архимеда. Рассмотрим тело АВ, погруженное в жидкость (рис. 11).
Подъемная сила Рп равна весу жидкости, вытесненной погруженным в нее телом, и направлена по вертикали снизу вверх. Это положение носит название закона Архимеда. На этом законе основана теория плавания тел. Подъемная сила приложена в центре погруженной части тела, называемом центром водоизмещения. В теории плавания тел используют два понятия: плавучесть и остойчивость. Плавучесть — это способность тела плавать. Остойчивость — способность плавающего тела восстанавливать нарушенное при крене равновесие после устранения сил, вызвавших крен. Плавучесть тела. В зависимости от соотношения между весом плавающего тела G и подъемной силой Рп возможны три состояния тела, погруженного в жидкость. Если G > Рп — тело тонет. Когда G < Рп — тело плавает в полупогруженном состоянии и когда G = Рп — тело плавает в погруженном состоянии. Остойчивость плавающего тела. При воздействии на плавающее тело внешних сил, например, ветра, крутого поворота, оно будет отклоняться от положения равновесия (давать крен). Если центр тяжести тела «с» расположен ниже центра водоизмещения, появляющаяся при крене пара сил противодействует ему, и после прекращения воздействия внешних сил тело принимает прежнее положение. Такое расположение центров соответствует остойчивому плаванию. Если центр тяжести «с» расположен выше центра водоизмещения, плавание будет неостойчивым. Тело будет выведено из состояния равновесия и уже не способно возвратиться в первоначальное положение, а наоборот, будет все более от него отклоняться. Наконец, при совпадении центров тяжести и водоизмещения тело будет находиться в состоянии безразличного равновесия.
7. Рассмотрим три сосуда разной формы, заполненные жидкостью до одного уровня hc. Все сосуды такие, что имеют одинаковую площадь дна. В соответствии с общей формулой определения силы, действующей на плоскую поверхность
можно вычислить силу, действующую на дно сосуда. Для всех трёх сосудов эти силы окажутся одинаковыми и независящими от веса жидкости в сосуде. Но на опору все сосуды будут действовать с разными силами, равными весу сосудов с жидкостью. Этот факт получил названиегидростатического парадокса.
8. Гидравлические машины гидростатического действия. В основу принципа действия многих гидравлических машин положены законы гидравлики. Одним из наиболее широко применяемых в технике законов является закон Паскаля. Гидравлический пресс (рис. 6) состоит из двух сообщающихся камер, в которых установлены поршни П1 и П2 площадью ω1 и ω2.
Эта сила будет сжимать тело, помещенное между поршнем П2 и неподвижным горизонтальным упором. Таким образом, сила давления Р1 приложенная к малому поршню П1 создает сжимающую силу Р2, превышающую силу Р1 во столько раз, во сколько площадь ω2 больше площади ω1. Гидравлический домкрат. Подъемы больших грузов на малую высоту можно легко осуществлять с применением гидравлических домкратов. Гидравлический домкрат состоит из цилиндра (сосуда) с большим поршнем и насоса с малым поршнем, который нагнетает в сосуд жидкость. Поршневой насос приводится в действие рычажным устройством. Давление поршня насоса передается жидкостью на большой поршень с грузом, вес которого во много раз превышает силу давления поршня насоса. Принцип работы гидравлического домкрата применяют в бульдозерах, канавокопателях, автокранах и в других строительных машинах. 9. Для измерения давления используют жидкостные (барометр, пьезометр, вакуумметр, дифманометр), механические (манометр, вакуумметр) и электрические приборы. Рассмотрим принцип действия основных из них. Барометр состоит из открытой чашки, заполненной ртутью, и стеклянной трубки, верхний конец которой запаян,
где Пьезометр - это прибор для измерения небольших давлений в жидкости при помощи высоты столба этой жидкости (рис.2.6).
По основному уравнению гидростатики
Вакуумметр - это U-образная стеклянная трубка, в колене которой имеется жидкость, тяжелее от той, которая
Пружинный манометр (рис.2.8) состоит из корпуса 5, штуцера 6, манометрической (пружинной) трубки 4, передающе-
10.Понятие о пьезометрической высоте и вакууме
Различают давление, которое соответствует абсолютному нулю, и давление атмосферное (рис.2.3). Относительно абсолютного нуля давление в любой точки жидкости называется абсолютным
Избыточным (манометрическим) называется давление, превышающее атмосферное (см.рис.2.3). Давление, недостающее до атмосферного, или разность между атмосферным
Рассмотрим закрытый сосуд1, заполненный жидкостью, на поверхности которой действует давление
Пьезометрическая высота
Аналогично определяется вакуумметрическая высота с учетом уравнения (2.6):
Плоскость П-П, давление во всех точках которой равно атмосферному, называется пьезометрической. Если сосуд открыт, то пьезометрическая плоскость совпадает со свободной поверхностью жидкости. 11. Эпюра давления. Для графического изображения закона изменения гидростатического давления по глубине служат эпюры давления. Площадь эпюры выражает силу давления, а центр тяжести эпюры — это точка, через которую проходит равнодействующая сила давления. При построении эпюр учитывают, что давление направлено нормально к стенке, а уравнение р = р0 + γh, характеризующее распределение гидростатического давления по глубине, является уравнением прямой. На рис. 7 показаны эпюры гидростатического давления (абсолютного и избыточного), действующего на вертикальную плоскую стенку АВ. Для их построения достаточно отложить в выбранном масштабе гидростатическое давление по горизонтальному направлению, совпадающему с направлением гидростатического давления, на поверхности жидкости и у дна, соединив концы этих отрезков прямой линией. Эпюра абсолютного гидростатического давления представляет собой трапецию, а эпюра избыточного гидростатического давления — треугольник. Если плоская стенка АВ, на которую действует жидкость, наклонена к горизонту под углом α (рис. 8), то основное уравнение гидростатики принимает следующий вид: рабс. = р0 + γh = р0 + γL sin α
В данном случае эпюры абсолютного и избыточного гидростатического давления представляют собой соответственно наклонную трапецию и наклонный треугольник. На рис. 9 показана эпюра избыточного гидростатического давления для вертикальной плоской стенки АВ, подверженной действию воды с двух направлений.
Давление жидкости на криволинейную поверхность. Рассмотрим действие избыточного гидростатического давления на криволинейную поверхность АВ (рис.10). Выделим на этой поверхности бесконечно малую площадку dω, центр тяжести которой погружен в жидкость на глубину h. На эту элементарную площадку нормально к криволинейной поверхности будет действовать сила избыточного гидростатического давления dP = γhdω, которую можно разложить на горизонтальную и вертикальную составляющие, т. е. на силы dPх и dPz.
Следовательно вертикальная составляющая равна весу жидкости в объёме тела давления. Полная сила избыточного гидростатического давления является равнодействующей её составляющих Pх и Pz и определяется по зависимости: Р =  Рис. 1 Площадь смоченной части стенки (abcd) равна w. Стенка наклоненак горизонту под углом a и симметрична относительно вертикальной оси; ширинастенки В.Направим оси y и x, как показано на рис. 1. Выделим на глубине h элементарную площадку Dw, в пределах которой гидростатическое давлениеможно считать всюду равным gh. Тогда сила давления на площадку Dw равна Dр=ghDw.Сила гидростатического давления на всю стенку площадью w равна суммеэлементарных сил давления Dр на площадки Dw, т.к. площадь wсостоит из суммы Dw. Рис. 1 Площадь смоченной части стенки (abcd) равна w. Стенка наклоненак горизонту под углом a и симметрична относительно вертикальной оси; ширинастенки В.Направим оси y и x, как показано на рис. 1. Выделим на глубине h элементарную площадку Dw, в пределах которой гидростатическое давлениеможно считать всюду равным gh. Тогда сила давления на площадку Dw равна Dр=ghDw.Сила гидростатического давления на всю стенку площадью w равна суммеэлементарных сил давления Dр на площадки Dw, т.к. площадь wсостоит из суммы Dw.  (1)Для нашего случая h=ysina, то по формуле (1) (1)Для нашего случая h=ysina, то по формуле (1)  Вынося постоянные величины g и sina за знак суммы получим Вынося постоянные величины g и sina за знак суммы получим  (2)где (2)где  - статическиймомент площади относительно оси х, равный - статическиймомент площади относительно оси х, равный  ( где yc – координата центра тяжести площади w)Подставим это выражение в формулу 2 ( где yc – координата центра тяжести площади w)Подставим это выражение в формулу 2  , но , но  тогда тогда  (3)Это уравнение следует читать так: сила гидростатического давления на плоскуюстенку, погруженную в жидкость, равна произведению площади стенки нагидростатическое давление в её центре тяжести.При определении силы абсолютного гидростатического давления формула 10 имеет вид (3)Это уравнение следует читать так: сила гидростатического давления на плоскуюстенку, погруженную в жидкость, равна произведению площади стенки нагидростатическое давление в её центре тяжести.При определении силы абсолютного гидростатического давления формула 10 имеет вид  (4) (4)
ЦЕНТР ДАВЛЕНИЯ Для полной характеристики силы давления необходимо знать еще ее точкуприложения, которая называется центром давления.Будем рассматривать только силы весового давления.Обратимся к рисунку 1. Силы давления Р приложены в некоторой точке D – центр давления, которая, как это будет доказано в дальнейшем, лежит несколькониже центра тяжести площади стенки. Для объяснения будем использовать теорему,известную из теоретической механики, о моменте равнодействующей, согласнокоторой момент равнодействующей силы относительно какой-то оси равен суммемоментов составляющих относительно той же оси. Для нашего случая это условиезаписывается в следующем виде: (5)где Р – сила давления (равнодействующая); yD – плечосилы Р относительно оси Ох; DP – сила давления на элементарнуюплощадку; y – плечо силы DP относительно оси Ох.Из предыдущего известно, что (5)где Р – сила давления (равнодействующая); yD – плечосилы Р относительно оси Ох; DP – сила давления на элементарнуюплощадку; y – плечо силы DP относительно оси Ох.Из предыдущего известно, что  , ,  Подставляя это выражение в условие 5 получим Подставляя это выражение в условие 5 получим   (6)Вынося из-под знака суммы постоянные величины g, sina и сокращаяна них, перепишем уравнение 6: (6)Вынося из-под знака суммы постоянные величины g, sina и сокращаяна них, перепишем уравнение 6:  отсюда отсюда 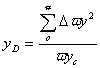 (7)где (7)где  = =  - осевой момент инерции площади w относительно оси х. Тогда выражение 7 можнонаписать так: - осевой момент инерции площади w относительно оси х. Тогда выражение 7 можнонаписать так:  (8)Из теоретической механики известно, что (8)Из теоретической механики известно, что   Подставляя значение Jx в выражение 8, получим: Подставляя значение Jx в выражение 8, получим:  (9)Из выражения 9 видно, что YD>YC, т.е. центрдавления всегда лежит ниже центра тяжести площади. ГРАФОАНАЛИТИЧЕСКОЕ ОПРЕДЕЛЕНИЕ СИЛЫ ДАВЛЕНИЯ, ДЕЙСТВУЮЩИХ НАПЛОСКИЕ ПРЯМОУГОЛЬНЫЕ СТЕНКИ Определение силы гидростатического давления на плоские стенки и центрадавления графоаналитическим путем предусматривает решение задачи частичноаналитическими способами. Рассмотрим случай плоской прямоугольнойвертикальной стенки (см. рисунок) (9)Из выражения 9 видно, что YD>YC, т.е. центрдавления всегда лежит ниже центра тяжести площади. ГРАФОАНАЛИТИЧЕСКОЕ ОПРЕДЕЛЕНИЕ СИЛЫ ДАВЛЕНИЯ, ДЕЙСТВУЮЩИХ НАПЛОСКИЕ ПРЯМОУГОЛЬНЫЕ СТЕНКИ Определение силы гидростатического давления на плоские стенки и центрадавления графоаналитическим путем предусматривает решение задачи частичноаналитическими способами. Рассмотрим случай плоской прямоугольнойвертикальной стенки (см. рисунок)  Рис. 2 Имеем вертикальную стенку (ас) шириной В, поддерживающую с однойстороны жидкость глубиной (h). Построим эпюру избыточногогидростатического давления, которая имеет вид прямоугольного треугольника (авс).На глубине h на стенке выделим элементарную площадку высотой Dh и шириной В. Площадь её равна Рис. 2 Имеем вертикальную стенку (ас) шириной В, поддерживающую с однойстороны жидкость глубиной (h). Построим эпюру избыточногогидростатического давления, которая имеет вид прямоугольного треугольника (авс).На глубине h на стенке выделим элементарную площадку высотой Dh и шириной В. Площадь её равна   .Элементарная сила давления на выделенную площадку равна .Элементарная сила давления на выделенную площадку равна  (10)Произведение (10)Произведение  (см.рисунок 2) есть часть площади эпюры давления, подставляя это значение ввыражение (10) получим (см.рисунок 2) есть часть площади эпюры давления, подставляя это значение ввыражение (10) получим 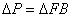 Сила гидростатического давления на всю стенку будет равна сумме элементарных сил DР, взятой в пределах площади. Сила гидростатического давления на всю стенку будет равна сумме элементарных сил DР, взятой в пределах площади.  (11)В нашем случае ширина стенки В – величина постоянная. Учитывая это мы получим (11)В нашем случае ширина стенки В – величина постоянная. Учитывая это мы получим  , но , но  и окончательнополучим: и окончательнополучим:  Таким образом сила гидростатического давления на плоскую прямоугольную стенкуравна площади эпюры гидростатического давления, умноженного на ширину стенки. Таким образом сила гидростатического давления на плоскую прямоугольную стенкуравна площади эпюры гидростатического давления, умноженного на ширину стенки.
13.Сила давления жидкости на плоские поверхности
Сила давления жидкости на погруженную в нее плоскую поверхность (рис.2.9) равна
Таким образом, полная сила давления на плоскую стенку равна произведению площади этой стенки на величину гидростатичес- кого давления Выражение (2.11) можно представить в виде
где
Сила Сила
где Для прямоугольника

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 Рис.1. Схема, поясняющая понятие
гидростатического давления
Рис.1. Схема, поясняющая понятие
гидростатического давления
 и выделим около нее малую площадку
и выделим около нее малую площадку  . В центре этой площадки действует сила
. В центре этой площадки действует сила  , представляющая собой равнодействующую сил, приложенных к различным точкам площадки
, представляющая собой равнодействующую сил, приложенных к различным точкам площадки 
 — средним гидростатическим давлением. Если уменьшать площадку
— средним гидростатическим давлением. Если уменьшать площадку 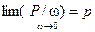
 Рис. 2. Схема к выводу основного
уравнения гидростатики
Рис. 2. Схема к выводу основного
уравнения гидростатики
 Рис. 3. Схема установки пьезометра
Рис. 3. Схема установки пьезометра
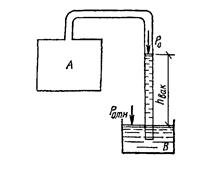 Рис. 4. Схема установки вакууметра
Рис. 4. Схема установки вакууметра
 Рис. 5. Схема установки ртутного манометра
Рис. 5. Схема установки ртутного манометра
 . Давление жидкости в I сосуде расписывается по формуле
. Давление жидкости в I сосуде расписывается по формуле  , где
, где  — высота столба в I сосуде. Давление жидкости во II сосуде
— высота столба в I сосуде. Давление жидкости во II сосуде  расписывается аналогично как
расписывается аналогично как  , где
, где  — высота столба во II сосуде. Так как система статична, то давления равны, и
— высота столба во II сосуде. Так как система статична, то давления равны, и  ,
, Рис.11. Схема действия сил на тело
погружённое в жидкость
Рис.11. Схема действия сил на тело
погружённое в жидкость
 ,
,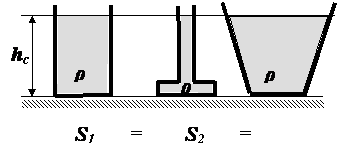
 Рис. 6. Схема гидравлического пресса
Рис. 6. Схема гидравлического пресса

 . Значение атмосфер-ного давления определяют по формуле
. Значение атмосфер-ного давления определяют по формуле
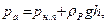 (2.9)
(2.9) - плотность ртути; h- высота подъема жидкости в трубке.
- плотность ртути; h- высота подъема жидкости в трубке.
 . (2.10)
. (2.10)
 на свободной поверхности жидкости, если трубка присоединена выше этой поверхности, вычисляют по формуле
на свободной поверхности жидкости, если трубка присоединена выше этой поверхности, вычисляют по формуле
 . (2.11)
. (2.11)
 .
.
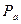 называется избыточным давлением и обозначается
называется избыточным давлением и обозначается  :
:
 (2.5)
(2.5) и абсолютным давлением
и абсолютным давлением  . (2.6)
. (2.6) , превышающее атмосферное давление
, превышающее атмосферное давление  , которая в гидравлике называется пьезометрической высотой, а сама трубка- пьезометром.
, которая в гидравлике называется пьезометрической высотой, а сама трубка- пьезометром.
 . (2.7)
. (2.7) . (2.8)
. (2.8) Рис. 7. Эпюры гидростатического давления,
действующего на вертикальную стенку
Рис. 7. Эпюры гидростатического давления,
действующего на вертикальную стенку
 Рис. 8. Эпюры гидростатического давления,
действующего на наклонную стенку
Рис. 8. Эпюры гидростатического давления,
действующего на наклонную стенку
 Рис.9. Эпюра гидростатического давления,
действующего на вертикальную стенку с двух сторон
Рис.9. Эпюра гидростатического давления,
действующего на вертикальную стенку с двух сторон
 Рис.10. Схема давления жидкости на криволинейную поверхность
Рис.10. Схема давления жидкости на криволинейную поверхность
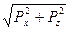
 (2.12)
(2.12)
 - глубина погружения центра тяжести смоченной части плоской поверхности; S-площадь смоченной части плоской поверхности;
- глубина погружения центра тяжести смоченной части плоской поверхности; S-площадь смоченной части плоской поверхности;
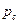 - гидростатическое давление в центре тяжести поверхности.
- гидростатическое давление в центре тяжести поверхности. (2.13)
(2.13) (2.14)
(2.14) (2.15)
(2.15) представляет собой силу поверхностного давления
представляет собой силу поверхностного давления  обусловлена давлением самой жидкости. Сила
обусловлена давлением самой жидкости. Сила  приложена в центре давления Д, координату которого определяют по формуле
приложена в центре давления Д, координату которого определяют по формуле , (2.16)
, (2.16) - момент инерции плоской фигуры относительно оси ОХ.
- момент инерции плоской фигуры относительно оси ОХ. (b-ширина, h-высота фигуры), для круга диаметром d
(b-ширина, h-высота фигуры), для круга диаметром d  .
.