
|
|
Перемещения и деформации стержня
При нагружении осевой растягивающей силой F стержень удлиняется на величину Dl , а размеры его сечения уменьшаются на величину Dв (см. рис.1.3). Обозначим: l/ - l = Dl – абсолютное удлинение (укорочение) стержня; в/ - в= Dв – абсолютное изменение размера сечения;
Очевидно, что деформации e и e/ являются безразмерными величинами. Из опыта известна связь между e и e/
либо в другой форме Здесь: n – коэффициент поперечной деформации (коэффициент Пуассона). Величина n является безразмерной и для каждого материала постоянна. Для изотропных материалов n изменяется в пределах сталь различных марок – n = 0,25 – 0,33 (обычно принимают n= 0,3); каучук натуральный – n = 0,47 (близок к несжимаемому материалу – n = 0,5); пробковое дерево – n » 0. Заметим, что знак «-» в формулах (1.6, 1.7) обусловлен различными знаками продольной и поперечной деформаций при положительном значении коэффициента Пуассона n (при растяжении величина e положительна, а e/ - отрицательна, при сжатии наоборот) Закон Гука Закон Гука формулируется следующим образом: до определенных пределов нагружения напряжения в точке тела прямо пропорциональны деформации. Аналитическая формулировка закона Гука при осевом растяжении (сжатии) имеет вид
Коэффициентом пропорциональности в законе Гука является модуль нормальной упругости (другие названия: модуль Юнга, модуль упругости I-го рода) – Е, который характеризует способность материала сопротивляться внешним силам (характеризует жесткость материала). Измеряется величина Е в тех же единицах, что и напряжения: Па, МПа. Значения Е для каждого материала постоянны. Для всех марок сталей величина Е примерно одинакова и составляет Е=2·105 МПа. Ниже, в таблице приведены значения Е для других характерных материалов
Используя формулу закона Гука (1.8), можно определить удлинение (укорочение) призматического стержня, у которого величина нормального усилия по длине не изменяется (N=const). Так, подставляя в (1.8), выражение для напряжения (1.5) получим формулу для удлинения (укорочения) призматического стержня
Заметим, что произведение Е А, стоящее в знаменателе формулы, называется жесткостью поперечного сечения стержня при растяжении-сжатии.
МЕХАНИЧЕСКИЕ ХАРАКТЕРИСТИКИ МАТЕРИАЛОВ
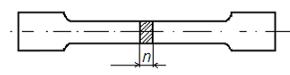
Механические характеристики материалов при расчетах на прочность, жесткость и устойчивость определяются из опытов, чаще всего, при растяжении-сжатии специальных образцов (рис.1.4):
Рис.1.4 Классификация конструкционных материалов Различают: пластичные, хрупко-пластичные и хрупкие материалы. Пластичные материалы – характеризуются существенными деформациями, предшествующими разрушению (чистые металлы: Cu, Al, Fe, конструкционные стали). Хрупкие материалы – характеризуются малыми деформациями, предшествующими разрушению (стекло, чугун, бетон, кирпич, керамика). Хрупко-пластичные материалы – занимают промежуточное место между пластичными и хрупкими (углеродистые инструментальные стали, ряд металлических сплавов, пластмасс и керамики.
I. Пластичные материалы Рассмотрим механические свойства пластичных материалов на примере широко распространенной в строительстве конструкционной стали Ст3.
Испытания на растяжение Испытания на растяжение проводятся в специальных либо универсальных испытательных машинах. При этом получают связь между нагрузкой (F)иудлинением(Dl) образца в диапазоне нагрузок от 0 до разрушения (рис.1.5).
Рис.1.5 Рис.1.6 Диаграмма «F - Dl» называетсядиаграммой растяжения (рис.1.6). Диаграмма включает в себя следующиеучастки: 1) линейный участок; 2) участок текучести (площадка текучести); 3) участок упрочнения (наклепа, нагартовки); 4) участок разрыва.
В пределах линейного участка деформации образца визуально не отмечаются. На участке текучести поверхность образца покрывается линиями Чернова-Людерса – мелкой визуально не фиксируемой сетью поверхностных микротрещин, ориентированных под углом 45° к оси образца (рис.1.7). Появление трещин проявляется визуально в том, что зеркальная поверхность полированного образец мутнеет. На этом же участке образец заметно удлиняется. При достижении Площадь, ограниченная диаграммой «F -Dl» и осью ОDl, определяет работу, затраченную на разрыв образца.
Рис.1.7 Диаграмма растяжения не может быть использована непосредственно для определения механических характеристик материала, поскольку они будут зависеть от размеров образца. Для определения характеристик материала ее перестраивают в диаграмму « Здесь:
Диаграмма напряжений
Рис.1.8 Выделяют три группы механических характеристик материала: характеристики прочности, пластичности, упругости (рис.1.8). 1. Характеристики прочности: - - - - Очевидно, что в процессе нагружения площадь сечения образца уменьшается (поэтому рассматриваемую диаграмму называют диаграммой условных напряжений). Если при построении диаграммы напряжение определять по формуле
где А – текущая площадь образца (с учетом его сужения), получим диаграмму истинных напряжений (на рис.1.8 изображена штриховой линией). 2. Деформации и характеристики пластичности: Полная деформация образца при напряжении
Основной характеристикой пластичности является остаточная деформация образца после разрыва – d (рис.1.8). Вторая характеристика – относительное сужение образца в месте разрыва – y
Величину
Упругие характеристики К упругим характеристикам относят: модуль Юнга (Е) и коэффициент Пуассона (ν), которые определяются на линейном участке диаграммы по формулам
Явление упрочнения При нагружении образца до напряжений, превышающих предел текучести (например, до точки «k» диаграммы, Механические характеристики стали Ст3: 1) характеристики прочности:
2) основная характеристика пластичности d = 0,22; 3) характеристики упругости: Е = 2×105 МПа, 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 Рис.1.3
Рис.1.3
 – относительное удлинение
(укорочение) или линейная продольная
деформация;
– относительное удлинение
(укорочение) или линейная продольная
деформация;
 - относительное изменение
поперечного размера или поперечная
деформация.
- относительное изменение
поперечного размера или поперечная
деформация.
 (1.6)
(1.6) (1.7)
(1.7) . Ниже приведены значения n для некоторых материалов:
. Ниже приведены значения n для некоторых материалов: . (1.8)
. (1.8)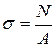 и выражение для деформации
и выражение для деформации  ,
, . (1.9)
. (1.9)


 - предельная нагрузка, выдерживаемая образцом;
- предельная нагрузка, выдерживаемая образцом;  - нагрузка разрыва.
- нагрузка разрыва. на образце возникает шейка (локальное сужение образца). На участке разрыва шейка интенсивно развивается, и при величине силы F =
на образце возникает шейка (локальное сужение образца). На участке разрыва шейка интенсивно развивается, и при величине силы F = 
 », которую называют диаграммой напряжений, либо, более строго, диаграммой условных напряжений (рис.1.8).
», которую называют диаграммой напряжений, либо, более строго, диаграммой условных напряжений (рис.1.8). ;
;  ;
; - исходная площадь образца;
- исходная площадь образца;  - исходная длина образца.
- исходная длина образца.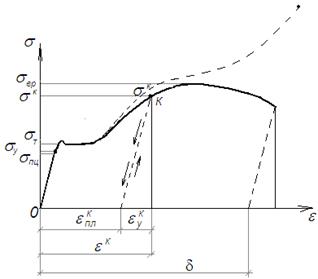
 - предел пропорциональности – наибольшее значение напряжений, при которых остается справедливым для материала закон Гука;
- предел пропорциональности – наибольшее значение напряжений, при которых остается справедливым для материала закон Гука; - предел упругости, – наибольшее значение напряжений, при которых материал остается упругим;
- предел упругости, – наибольшее значение напряжений, при которых материал остается упругим; - предел текучести – напряжения, при которых деформации развиваются без изменения нагрузки;
- предел текучести – напряжения, при которых деформации развиваются без изменения нагрузки; - предел прочности (предел временного сопротивления) – наибольшее значение условных напряжений в образце.
- предел прочности (предел временного сопротивления) – наибольшее значение условных напряжений в образце. ,
, определяется по формуле (рис.1.8)
определяется по формуле (рис.1.8) , где
, где - пластическая (остаточная) деформация;
- пластическая (остаточная) деформация; - упругая деформация.
- упругая деформация. . Здесь: Аш – площадь шейки в месте разрыва.
. Здесь: Аш – площадь шейки в месте разрыва. - используют для классификации материала: если
- используют для классификации материала: если  ,
,  .
. , см. рис.1.8), и последующей разгрузке отмечается явление упрочнения (наклепа или нагартовки), которое заключается в увеличении характеристик прочности (
, см. рис.1.8), и последующей разгрузке отмечается явление упрочнения (наклепа или нагартовки), которое заключается в увеличении характеристик прочности (  ) и снижении основной характеристики пластичности (
) и снижении основной характеристики пластичности ( 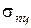 = 200 МПа;
= 200 МПа;  = 200 МПа;
= 200 МПа; = 400 МПа;
= 400 МПа; (0,3).
(0,3).