
|
|
I. Гипотезы о свойствах материала1. Гипотеза сплошности – реальный материал с дискретной структурой заменяем сплошной средой с осредненными физико-механическими характеристиками (дискретную атомистическую природу вещества во внимание не принимаем). 2. Гипотеза однородности и изотропности – физико-механические свойства материала в каждой точке (однородность) и во всех направлениях (изотропность) одинаковы. 3. Гипотеза идеальной упругости – материал, до определенных пределов нагружения, является абсолютно упругим. 4. Гипотеза о линейной зависимости между напряжениями и деформациями в точке – между напряжениями и деформациями в точке, до определенных пределов нагружения, справедлива линейная зависимость. Эта гипотеза обусловливает физическую линейность задач СМ и отражает важнейший в СМ физический закон – закон Гука. II. Гипотезы о характере деформаций 5. Гипотеза о естественном ненапряженном состоянии тела – при отсутствии нагрузки (внешних сил) напряжения в теле отсутствуют. 6. Гипотеза о малости деформации – перемещения при нагружении малы по сравнению с характерными минимальными размерами тела. Эта гипотеза обусловливает геометрическую линейность задач СМ. 7. Гипотеза плоских сечений Якоба Бернулли – сечения плоские и перпендикулярные к оси бруса до нагружения остаются плоскими и перпендикулярными к оси бруса после нагружения.
Расчетные принципы сопротивления материалов I. Принцип независимости действия сил – эффект от действия системы внешних сил (температуры) равен сумме эффектов от действия каждого из силовых факторов в отдельности (рис.0.9).
Этот принцип базируется на гипотезе о линейной зависимости между напряжениями и деформациями в точке и гипотезе о малости деформаций.
Vc=Vc(F1)+Vc(F2) Рис.0.9 II. Принцип начальных размеров (замороженности) – при рассмотрении равновесия нагруженного тела изменения его размеров и конфигурации во внимание не принимаются (уравнения равновесия формируются для недеформированного тела) (рис.0.10). Этот принцип базируется на гипотезе о малости деформаций.
Рис.0.10 III. Принцип Сен-Венана – напряженно-деформируемое состояние (НДС) в точках, удаленных от мест приложения нагрузки, не зависит от особенностей ее приложения, а определяется равнодействующей нагрузки (рис.0.11).
Рис.0.11 Следствие: При решении практических задач систему действующих внешних сил можно заменять эквивалентной ей системой, с точки зрения принципа Сен-Венана.
Напряжения и деформации в зоне приложения нагрузки называются местными (эти напряжения, в принципе, могут быть определены методами теории упругости). РАЗДЕЛ 1 ОСЕВОЕ РАСТЯЖЕНИЕ (СЖАТИЕ) СТЕРЖНЕЙ Если в сечении стержня возникает только нормальная сила – N, имеет место осевое (центральное) растяжение либо сжатие. Внешние силы в этом случае должны действовать вдоль оси либо приводиться к равнодействующей, направленной вдоль оси.
Усилия и напряжения Рассмотрим призматический стержень, который растягивается силой F, приложенной вдоль оси к нижнему торцу стержня (рис.1.1).
Рис.1.1 Используя метод сечения, определим нормальное усилие в произвольном сечении стержня – N. Собственный вес стержня не учитываем. Начало координат помещаем на свободном краю стержня.
Рис.1.2 Суммируя элементарные усилия (интегрируя) по всей площади поперечного сечения, получим
Из формулы (1.3) определить нормальное напряжение s невозможно, поскольку неизвестен закон распределения s по сечению (говорят в этой связи, что задача определения s в брусе является внутренне статически неопределимой). Для решения задачи необходимо использовать дополнительные соображения, в частности, допущения и гипотезы, касающиеся характера деформации стержня: 1) гипотезу плоских сечений (Я.Бернулли); 1) допущение о ненадавливании продольных волокон друг на друга. Согласно гипотезе Я.Бернулли, плоское сечения ав (см.рис.1.1) переместится параллельно в положение а/в/, при этом, очевидно, что деформации всех продольных волокон будут одинаковы. Поскольку, согласно допущению 2, эти волокна не взаимодействуют друг с другом, в соответствии с законом Гука, напряжения в них будут одинаковы, т.е. s будут равномерно распределены по сечению (s = const). Это позволяет вынести величину s в формуле (1.3) за знак интеграла
Учитывая, что
Правило знаков для N и s : при осевом растяжении N и s положительны; при сжатии – отрицательны. Рекомендации: на расчетной схеме метода сечений целесообразно задавать положительные направления N и s, обусловливающие растяжение рассматриваемого элемента (в направлении внешней нормали к сечению). Тогда из уравнений равновесия знак N и s будет получаться автоматически. Отметим, что, поскольку при осевом растяжении-сжатии отсутствуют поперечные составляющие внешней нагрузки, в поперечном сечении стержня касательные напряжения – t также отсутствуют, т.е.

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|




 , откуда
, откуда 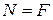 . (1.1)
Заметим, что усилие N является равнодействующей элементарных усилий (dN), распределенных по сечению. Величина этих элементарных усилий может быть определена по формуле
dN=s dA , (1.2)
где s - нормальное напряжение, dA – площадь элементарной площадки сечения (рис.1.2).
. (1.1)
Заметим, что усилие N является равнодействующей элементарных усилий (dN), распределенных по сечению. Величина этих элементарных усилий может быть определена по формуле
dN=s dA , (1.2)
где s - нормальное напряжение, dA – площадь элементарной площадки сечения (рис.1.2).
 либо, с учетом (2)
либо, с учетом (2) 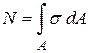 . (1.3)
. (1.3) . (1.4)
. (1.4)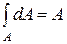 , получаем из (1.4) формулу для напряжений при осевом растяжении-сжатии
, получаем из (1.4) формулу для напряжений при осевом растяжении-сжатии . (1.5)
. (1.5) .
.