|
Погружение в тень тяготения
В смысле затраты работы совершенно безразлично, перенесете ли вы груз с Земли в бесконечно удаленную точку, или в такое место (хотя бы и весьма близкое), где он вовсе не притягивается Землей. И в том, и в другом случаях вы совершили бы одинаковую работу, ибо величина ее зависит не от длины пройденного пути, а только от различия силы притяжения в крайних точках пути. При переносе тела в бесконечность работа эта производится постепенно, на всем бесконечно длинном пути, а при переносе за экран тяготения такое же количество энергии затрачивается в те несколько мгновений, пока совершается этот перенос. Надо ли говорить, что практически вторую работу было бы гораздо труднее произвести, чем первую?
Теперь становится очевидной безнадежность фантастического проекта Уэльса. Романист не подозревал, что столь простое на вид действие, как перенесение тела за экран, непроницаемый для тяготения — представляет собою неимоверно трудную механическую задачу: ведь для этого надо сделать такое же усилие, как и для того, чтобы удалить тело с Земли в бесконечность!
Уэльс упустил из виду, что задвинуть заслонки его снаряда вовсе не так легко и просто, как захлопнуть дверцу кареты: в тот краткий миг, когда закрывается последняя заслонка и пассажиры отделяются от весомого мира, — должна быть выполнена работа, равная работе перенесения полного веса пассажиров в бесконечность. А так как два человека весят свыше 100 килограммов, то, значит, задвигая заслонки снаряда, герои романа должны совершить работу ни мало, ни много — в 600 миллионов килограммометров! Это почти так же легко выполнить, как втащить броненосец на купол Исаакиевского собора, и притом в течение всего нескольких секунд. Будь мы были подобными богатырями, мы могли бы без всякого, кеворита" буквально прыгнуть с Земли на Луну… Не приходилось бы долго размышлять над проблемой межпланетных путешествий.
Безвыходный круг
Итак, идея странствовать во вселенной под защитою вещества, непроницаемого для тяготения, приводит нас к тому, что в логике называется „безвыходным кругом". Чтобы воспользоваться таким веществом, необходимо преодолеть притяжение Земли — т.-е. выполнить именно то, ради чего и придуман экран тяготения. Следовательно, вещество, непроницаемое для тяготения, бесполезно для небесных путешествий.
5. Можно ли ослабить земную тяжесть?
Если несбыточны надежды укрыться от силы тяжести, то, быть-может, существуют способы хотя бы ослабить тяжесть на земной поверхности?
Увеличить объем Земли
Казалось бы, простой и ясный закон Ньютона не допускает подобной возможности даже в теории: сила притяжения зависит ведь от массы земного шара, которую уменьшить мы не в состоянии. Однако, это не так. Речь идет о напряжении тяжести на поверхности нашей планеты, а оно, как известно, зависит не от одной лишь массы, но также и от расстояния до центра земного шара, т.е. от величины земного радиуса. Если бы мы могли разрыхлить земной шар настолько, чтобы, увеличившись в объеме, он имел радиус, например, вдвое больше, чем теперь, то напряжение тяжести на поверхности такого шара стало бы вчетверо меньше. В самом деле: находясь на поверхности Земли, мы были бы вдвое дальше от притягивающего центра (шарообразные тела притягивают так, как будто вся их масса сосредоточена в центре). Выгода от подобного грандиозного переустройства обитаемой нами планеты получилась бы еще и та, что поверхность земного шара увеличилась бы при этом в четыре раза. Людям жилось бы на Земле буквально вчетверо свободнее и вчетверо легче.
Разумеется, ни современная техника, ни, вероятно, и будущая не в состоянии осуществить ничего подобного.
Миллионы лет назад
Любопытно, однако, что некогда, — в древние геологические эпохи, — радиус нашей планеты был действительно больше, нежели теперь; тогда и напряжение тяжести было соответственно слабее. Как утверждают геологи (теория Зюсса), горы на земном шаре образовались вследствие того, что наша планета, охлаждаясь, уменьшалась в объеме; при этом земная кора сморщивалась, как кожа иссохшего яблока. Морщины эти и есть горы. Если мысленно расправить все складчатые горы земного шара, то определится, насколько поверхность нашей планеты была некогда больше, нежели теперь. Этим путем вычислено, что в древнейшую геологическую эпоху (альгонкинскую) радиус земного шара был на 1/4 больше, нежели теперь. Мы знаем, что с удалением от центра напряжение тяжести уменьшается пропорционально квадрату расстояния. Значит, если поверхность Земли была тогда в  дальше от центра, чем теперь, то напряжение тяжести должно измениться в дальше от центра, чем теперь, то напряжение тяжести должно измениться в  раз, т.е. составляло приблизительно раз, т.е. составляло приблизительно 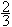 нынешней силы тяжести. Вы видите, что не всегда тяжесть на Земле была такой, как теперь: миллионы лет тому назад нынешний пуд весил на Земле всего около 25 фунтов. Приходится только пожалеть, что мы не жили на Земле несколькими миллионами лет ранее, когда задачу межпланетных путешествий можно было разрешить легче, нежели теперь… нынешней силы тяжести. Вы видите, что не всегда тяжесть на Земле была такой, как теперь: миллионы лет тому назад нынешний пуд весил на Земле всего около 25 фунтов. Приходится только пожалеть, что мы не жили на Земле несколькими миллионами лет ранее, когда задачу межпланетных путешествий можно было разрешить легче, нежели теперь…
Ускорить вращение Земли
Механика указывает и другой путь к ослаблению земной тяжести. Этот способ состоит в том, чтобы ускорить быстроту вращения Земли вокруг оси. Уже и теперь центробежная сила, возникающая при вращении земного шара, уменьшает вес всякого тела на экваторе на  долю. В соединении с другой причиной (вздутием земного шара у экватора) центробежная сила действует так, что все тела на экваторе весят на долю. В соединении с другой причиной (вздутием земного шара у экватора) центробежная сила действует так, что все тела на экваторе весят на  % меньше, чем близ полюсов. Паровоз, весящий в Москве 10.000 пудов, становится по прибытии в Архангельск на 10 пудов тяжелее, а в Одессу — настолько же легче. Партия угля в 300.000 пудов, доставленная с Шпицбергена в какой-нибудь экваториальный порт, уменьшилась бы в весе на 1.200 пудов, если бы приемщику пришла фантазия принять груз, пользуясь пружинными весами, выверенными на Шпицбергене. Броненосец, весивший в Архангельске 20.000 тонн, становится по прибытии в экваториальные воды легче на 80 тонн, т.-е. почти на 5.000 пудов; но это, конечно, остается неощутительным, так как соответственно легче делаются и все другие тела, не исключая и воды в океане. Всю эту разницу веса похищает, главным образом, центробежная сила: на экваторе она несколько больше, чем в высоких широтах, где точки земной поверхности при вращении Земли описывают гораздо меньшие круги. % меньше, чем близ полюсов. Паровоз, весящий в Москве 10.000 пудов, становится по прибытии в Архангельск на 10 пудов тяжелее, а в Одессу — настолько же легче. Партия угля в 300.000 пудов, доставленная с Шпицбергена в какой-нибудь экваториальный порт, уменьшилась бы в весе на 1.200 пудов, если бы приемщику пришла фантазия принять груз, пользуясь пружинными весами, выверенными на Шпицбергене. Броненосец, весивший в Архангельске 20.000 тонн, становится по прибытии в экваториальные воды легче на 80 тонн, т.-е. почти на 5.000 пудов; но это, конечно, остается неощутительным, так как соответственно легче делаются и все другие тела, не исключая и воды в океане. Всю эту разницу веса похищает, главным образом, центробежная сила: на экваторе она несколько больше, чем в высоких широтах, где точки земной поверхности при вращении Земли описывают гораздо меньшие круги.
Весьма нетрудно доказать, что если бы Земля вращалась в 17 раз быстрее, чем теперь, то центробежная сила на экваторе увеличилась бы 17 X 17, т.-е. почти в 290 раз. Если вы вспомните, что центробежная сила теперь похищает у тел как-раз долю их веса, то поймете, что на экваторе такой быстро вращающейся Земли тела совсем не имели бы веса! Стоило бы тогда лишь достичь экватора, чтобы, слегка оттолкнувшись здесь, быть отброшенным в мировое пространство. Задача межпланетных путешествий разрешалась бы крайне просто. А если бы Земля вращалась еще быстрее, то мы сделались бы небесными странниками поневоле, так как инерция вращения сама отбросила бы нас в бездонную глубь неба. Людям приходилось бы задумываться уже над проблемой „земных", а не межзвездных странствований.
Но в силах ли мы заставить обитаемый нами земной шар вращаться быстрее, нежели теперь? Ведь это значит совершить нечто вроде чуда Иисуса Навина — приказать Солнцу изменить свой (кажущийся) дневной путь по небесному своду!
Многим читателям, без сомнения, приятно будет узнать, что теоретически это в нашей власти. При помощи довольно простого приема люди могли бы ускорить или, если угодно, замедлить вращение земного шара.
Придется, однако, начать несколько издалека, чтобы объяснить эту возможность.
Вам случалось, вероятно, замечать, что когда, спеша выйти на берег, вы идете по дну причалившей лодки, она, к немалой досаде вашей, сама отодвигается от берега. Этим неприятным сюрпризом вы обязаны тому закону механики, который называется „законом действия и противодействия". Закон состоит в том, что всякая действующая сила всегда вызывает равную силу противодействия. Что происходит, когда вы идете по дну лодки? Вы отталкиваете свое тело от опоры; вместе с тем отталкивается назад и сама опора. При ходьбе по неподвижному полу этого не замечается, так как отталкивающее усилие уничтожается сопротивлением неподвижной опоры.
Не заметите вы обратного перемещения и в том случае, когда лодка очень велика или тяжело нагружена: это потому, что одна и та же сила сообщает различным телам различное движение, в зависимости от их массы — тяжелое тело она перемещает с меньшею скоростью, нежели легкое. Переходя по палубе большого парохода от кормы к носу, вы также отталкиваете ногами все судно назад; но скорость этого перемещения, даже если бы ему не препятствовало трение о воду, была бы ничтожна: во столько же раз меньше скорости вашего собственного перемещения, во сколько раз пароход тяжелее вас самих. Но вернемся к нашей лодке. Представьте себе, что она имеет не удлиненную форму, а форму большой плавающей тарелки, и вообразите, что вы ходите кругом вдоль борта такой круглой лодки. Что при этом произойдет с ней? Догадаться не трудно: она придет во вращательное движение в обратном направлении, т. е., отталкиваясь ногами, вы, подобно лошади на топчаке, заставите ее вращаться. Проделав тот же маневр на палубе большого парохода, вы, конечно, не приведете его во вращение: масса такой громады слишком велика по сравнению с массой вашего тела; да и, кроме того, усилие ваших ног должно при этом преодолеть трение погруженной части судна о воду. И все же, теоретически рассуждая, некоторое перемещение достижимо: чем дольше вы будете кружиться по палубе, тем на больший угол повернется пароход. Возможно, что, сделав миллион кругов, вы повернете пароход на некоторую долю градуса… Чем значительнее груз, перемещаемый по палубе, тем большую силу затратите вы на его перемещение, а следовательно, тем сильнее будет и отталкивающее действие. Запрягши слонов в пушки и заставив их в течение многих суток кружиться по палубе, вы добились бы менее ничтожных результатов, чем кружась сами.
Вот небольшой приборчик (см. черт.), помощью которого можно наглядно иллюстрировать это отталкивающее действие движущегося тела на опору. Миниатюрный заводной паровозик бегает по кольцеобразным рельсам, укрепленным на легкоподвижном столике. И можно прямо видеть при этом, как весь столик сам вращается в обратную сторону.
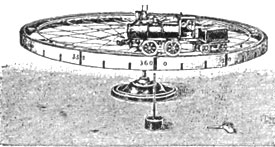
Игрушечный паровозик, иллюстрирующий отталкивательное действие движущегося тела на опору: когда паровозик бежит по рельсам, подвижная платформа вращается в обратную сторону.
Мы подошли, наконец, вплотную к интересующему нас вопросу. Вообразите, что по экватору или по параллельным кругам Земли с востока на запад совершается непрерывное перемещение грузов: мчатся поезда, плывут пароходы, течет вода в каналах и т. д. — все в одном и том же направлении. Как отразится это на вращении Земли? После всего сказанного ответ ясен. Земля сама вращается с запада на восток; перемещение грузов на запад должно сообщить ей добавочное вращение в восточную сторону; следовательно, Земля будет вращаться быстрее. Значит, мы можем сократить продолжительность суток! Теоретически, как видите, это вполне в нашей власти; практически же осуществить это трудно по многим причинам, и прежде всего за недостатком времени. Масса тех паровозов, пароходов и той воды, которые будут перемещаться по земной поверхности, так мала по сравнению с колоссальной массой земного шара, что пройдут тысячи веков, прежде чем длина суток изменится на ничтожную долю секунды. А ведь нам нужно сократить сутки в 17 раз!
Впрочем, если бы выполнение подобного проекта и оказалось по силам человечеству, то, вращаясь столь быстро, земной шар под действием огромной центробежной силы расплющился бы в диск (в плоскости своего экватора), а, быть-может, даже еще ранее разлетелся бы на части, как чересчур быстро заверченный жернов.
Возможность путешествовать в межзвездных пространствах была бы приобретена слишком дорогой ценой…
6. Вопреки тяжести. — На волнах света
Из трех мыслимых способов борьбы с тяготением мы рассмотрели и отвергли два: способ защиты от тяготения и способ ослабления земной тяжести. Мы убедились, что ни тот, ни другой не дают человечеству надежды успешно разрешить заманчивую проблему межпланетных полетов. Бесплодны всякие попытки укрыться от силы тяготения; безнадежно стремление ослабить напряжение тяжести. Остается одно: искать средство преодолеть тяготение и покинуть нашу планету вопреки ее притяжению.
Проектов подобного рода существует несколько. Для умов, практически настроенных, они, без сомнения, интереснее всяких других, так как их авторы не измышляют никаких фантастических веществ, в роде „экрана тяготения", не предлагают ни переделать земной шар, ни изменить скорость его вращения. Забегая вперед, я позволяю себе заинтриговать нетерпеливого читателя сообщением, что один из проектов типа: „вопреки тяжести" имеет шансы осуществиться в более или менее недалеком будущем.
Световое давление
Самый юный проект рассматриваемой категории предлагает воспользоваться для межпланетных перелетов давлением световых лучей. Лицам, мало знакомым с физикой, должно казаться невероятным, чтобы нежные, невесомые лучи света могли оказывать давление на озаряемые ими предметы. Между тем, одной из величайших заслуг безвременно скончавшегося гениального русского физика П. Н. Лебедева было то, что он доказал на опыте существование отталкивающей силы лучей света. Свет есть явление волнообразное, а всякая волнующаяся среда оказывает давление на встречаемую преграду.
В посмертной работе своей о световом давлении проф. П. Н. Лебедев писал:
„Давление волнующейся жидкости на препятствия, задерживающие распространение волн, легко наблюдать, если во время купания (в ванне или в пруде) ритмическим движением руки возбуждать волны и заставлять их отражаться от плавающего тела (бруска дерева): как только волны дойдут до бруска и начнут от него отражаться, так тотчас же брусок начинает двигаться с заметною скоростью в направлении распространения волн. Если на поверхности воды плавают мелкие предметы (например, опилки), которые волн не задерживают, то легко видеть, что волны двигают их вверх и вниз, но не увлекают с собою, и что, следовательно, движение плавающего тела обусловлено только силами падающих на него волн, а не движением самой жидкости".
Всякое светящееся тело — будь то свеча на вашем столе, электрическая лампа, раскаленное солнце или даже темное тело, испускающее невидимые лучи — давит своими лучами на озаряемые им тела. П. Н. Лебедеву удалось измерить силу давления, оказываемого солнечными лучами на освещаемые ими земные предметы: в мерах веса она составляет около ½ миллиграмма для площади в квадратный метр. Если умножить полмиллиграмма на число квадратных метров озаряемой Солнцем половины земного шара, мы получим весьма внушительный груз: 3½ миллиона пудов!
Такова величина силы, с которой Солнце давлением своих лучей постоянно отталкивает нашу планету. Взятая сама по себе, эта сила огромна; она подавляет воображение. Но в мире все относительно, и если сравнить ее с величиною солнечного притяжения, то окажется, что сила в 3½ миллиона пудов не может иметь ни малейшего влияния на движение земного шара, ибо она в 60 биллионов раз слабее силы солнечного притяжения! Далекий Сириус, от которого свет странствует к нам 10 лет, притягивает Землю с гораздо большею силою — 600 миллионов пудов — между тем планета наша словно не чувствует этого!
Однако, чем меньше тело, тем большую долю силы притяжения составляет сила светового давления. И вы поймете, почему это, если вспомните, что притяжение пропорционально массе тела, световое же давление пропорционально его поверхности. Уменьшите мысленно земной шар так, чтобы поперечник его стал вдвое меньше. Объем, а следовательно и масса Земли уменьшатся в 2 X 2 X 2 = 8 раз, поверхность же уменьшится лишь в 2 X 2 = 4 раза; притяжение ослабеет в 8 раз — пропорционально уменьшению массы; световое же давление уменьшится соответственно поверхности, т.-е. всего лишь в 4 раза. Вы видите, что притяжение ослабело более значительно, чем световое давление. Уменьшите Землю еще вдвое — получится снова выгода в пользу светового давления.
Если вы будете продолжать и далее такое уменьшение, т.-е. будете достаточно долго длить это неравное состязание кубов с квадратами, то неизбежно дойдете до таких мелких частиц, для которых световое давление, наконец, сравняется с притяжением. Подобная частица не будет уже притягиваться Солнцем — притяжение уничтожится равным отталкиванием. Вычислено, что для шарика плотности воды это должно иметь место в том случае, если поперечник его равен ½ миллионной доли миллиметра.
Не нашли, что искали? Воспользуйтесь поиском по сайту:
©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|


 дальше от центра, чем теперь, то напряжение тяжести должно измениться в
дальше от центра, чем теперь, то напряжение тяжести должно измениться в  раз, т.е. составляло приблизительно
раз, т.е. составляло приблизительно 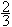 нынешней силы тяжести. Вы видите, что не всегда тяжесть на Земле была такой, как теперь: миллионы лет тому назад нынешний пуд весил на Земле всего около 25 фунтов. Приходится только пожалеть, что мы не жили на Земле несколькими миллионами лет ранее, когда задачу межпланетных путешествий можно было разрешить легче, нежели теперь…
нынешней силы тяжести. Вы видите, что не всегда тяжесть на Земле была такой, как теперь: миллионы лет тому назад нынешний пуд весил на Земле всего около 25 фунтов. Приходится только пожалеть, что мы не жили на Земле несколькими миллионами лет ранее, когда задачу межпланетных путешествий можно было разрешить легче, нежели теперь… долю. В соединении с другой причиной (вздутием земного шара у экватора) центробежная сила действует так, что все тела на экваторе весят на
долю. В соединении с другой причиной (вздутием земного шара у экватора) центробежная сила действует так, что все тела на экваторе весят на  % меньше, чем близ полюсов. Паровоз, весящий в Москве 10.000 пудов, становится по прибытии в Архангельск на 10 пудов тяжелее, а в Одессу — настолько же легче. Партия угля в 300.000 пудов, доставленная с Шпицбергена в какой-нибудь экваториальный порт, уменьшилась бы в весе на 1.200 пудов, если бы приемщику пришла фантазия принять груз, пользуясь пружинными весами, выверенными на Шпицбергене. Броненосец, весивший в Архангельске 20.000 тонн, становится по прибытии в экваториальные воды легче на 80 тонн, т.-е. почти на 5.000 пудов; но это, конечно, остается неощутительным, так как соответственно легче делаются и все другие тела, не исключая и воды в океане. Всю эту разницу веса похищает, главным образом, центробежная сила: на экваторе она несколько больше, чем в высоких широтах, где точки земной поверхности при вращении Земли описывают гораздо меньшие круги.
% меньше, чем близ полюсов. Паровоз, весящий в Москве 10.000 пудов, становится по прибытии в Архангельск на 10 пудов тяжелее, а в Одессу — настолько же легче. Партия угля в 300.000 пудов, доставленная с Шпицбергена в какой-нибудь экваториальный порт, уменьшилась бы в весе на 1.200 пудов, если бы приемщику пришла фантазия принять груз, пользуясь пружинными весами, выверенными на Шпицбергене. Броненосец, весивший в Архангельске 20.000 тонн, становится по прибытии в экваториальные воды легче на 80 тонн, т.-е. почти на 5.000 пудов; но это, конечно, остается неощутительным, так как соответственно легче делаются и все другие тела, не исключая и воды в океане. Всю эту разницу веса похищает, главным образом, центробежная сила: на экваторе она несколько больше, чем в высоких широтах, где точки земной поверхности при вращении Земли описывают гораздо меньшие круги.