Цилиндры второго порядка.
Существует три типа цилиндров второго порядка: эллиптический
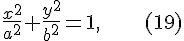
гиперболический
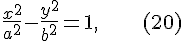
параболический
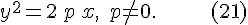
Эллиптический, гиперболический и параболический цилиндры суть поверхности, образованные прямыми линиями, проходящими через точки эллипса, гиперболы и параболы перпендикулярно плоскости каждой из этих линий. Эти линии - эллипс, гипербола, парабола - называются направляющими, а прямые, лежащие на поверхности цилиндра, - его образующими.
Для цилиндров, заданных уравнениями  , ,  , ,  , направляющими линиями являются соответственно эллипс , направляющими линиями являются соответственно эллипс
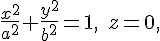
гипербола

парабола
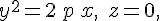
а образующие параллельны оси  . .
Определение 8.1. Прямая, все точки которой лежат на поверхности второго порядка, называется прямолинейной образующей этой поверхности.
Мы знаем, что конические и цилиндрические поверхности второго порядка имеют прямолинейные образующие, причем каждая из этих поверхностей может быть образована движением прямой в пространстве. Оказывается, что среди всех поверхностей второго порядка, кроме цилиндра, конуса и пар плоскостей, прямолинейными образующими обладают еще однополостный гиперболоид и гиперболический параболоид, причем, так же как в случае цилиндра и конуса, обе эти поверхности могут быть образованы движением прямой в пространстве.
ТЕОРЕМА 8.1. Через каждую точку однополостного гиперболоида проходят две и только две его прямолинейные образующие.
Доказательство. Пусть  --- произвольная точка однополостного гиперболоида --- произвольная точка однополостного гиперболоида
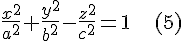
и
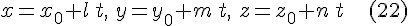
параметрические уравнения проходящей через нее прямой. Чтобы найти точки, общие поверхности  и прямой и прямой  , подставим в уравнение , подставим в уравнение  вместо вместо  и и  их выражения из формул их выражения из формул  : :
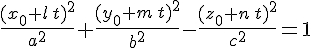
или
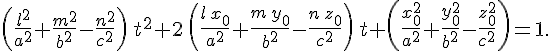
Так как точка  лежит на поверхности лежит на поверхности  , то , то
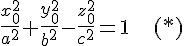
и последнее уравнение принимает вид
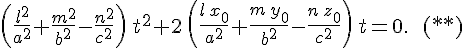
Для того чтобы прямая  целиком лежала на поверхности целиком лежала на поверхности  , необходимо и достаточно, что все ее точки лежали на этой поверхности, т.е. чтобы уравнение , необходимо и достаточно, что все ее точки лежали на этой поверхности, т.е. чтобы уравнение  удовлетворялось при всех значениях удовлетворялось при всех значениях  , а это возможно тогда и только тогда, когда оба коэффициента при , а это возможно тогда и только тогда, когда оба коэффициента при  и и  равны нулю: равны нулю:

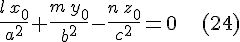
Мы получили два уравнения относительно координат  направляющего вектора прямой направляющего вектора прямой  . Из уравнения . Из уравнения  следует, что следует, что  , так как в противном случае , так как в противном случае  мы имели бы также мы имели бы также  , что противоречит определению направляющего вектора прямой линии. Так как направляющий вектор прямой определяется с точностью до коллинеарности и по доказанному , что противоречит определению направляющего вектора прямой линии. Так как направляющий вектор прямой определяется с точностью до коллинеарности и по доказанному  , то можно положить , то можно положить  . Тогда система уравнений . Тогда система уравнений  и и  примет вид примет вид
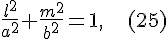

Покажем, что эта система имеет два действительных и различных решения. В самом деле, рассмотрим тождество Лагранжа
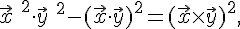
которое в координатной форме для векторов
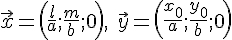
имеет вид
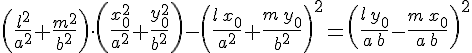
Из последнего равенства в силу уравнений  , , 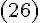 и и  находим находим
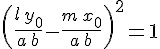
или
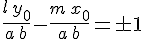
Итак, для определения координат  и и  направляющего вектора направляющего вектора  прямолинейных образующих однополостного гиперболоида прямолинейных образующих однополостного гиперболоида  , проходящих через точку , проходящих через точку  , мы имеем систему , мы имеем систему
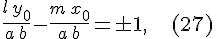
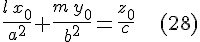
эквивалентную системе  , , 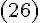 . Выбирая в правой части уравнения . Выбирая в правой части уравнения  , знак , знак  , получим первое решение этой системы, которое вместе с равенством , получим первое решение этой системы, которое вместе с равенством  дает координаты одного направляющего вектора прямолинейной образующей однополостного гиперболоида: дает координаты одного направляющего вектора прямолинейной образующей однополостного гиперболоида:
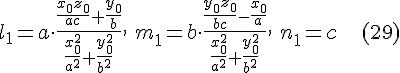
Выбирая в правой части уравнения  , знак , знак  , получим второе решение этой системы, которое вместе с равенством , получим второе решение этой системы, которое вместе с равенством  дает координаты другого направляющего вектора прямолинейной образующей однополостного гиперболоида: дает координаты другого направляющего вектора прямолинейной образующей однополостного гиперболоида:
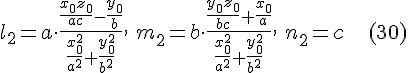
Таким образом, найдены направляющие векторы  и и  прямолинейных образующих однополостного гиперболоида прямолинейных образующих однополостного гиперболоида  , проходящие через его точку , проходящие через его точку  . Нетрудно видеть, что . Нетрудно видеть, что  и и  неколлинеарны. Теорема доказана. неколлинеарны. Теорема доказана.
Каждая из образующих пересекает плоскость 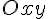 в точке, лежащей на горловом эллипсе. Поэтому за начальную точку каждой образующей всегда можно взять точку ее пересечения с горловым эллипсом в точке, лежащей на горловом эллипсе. Поэтому за начальную точку каждой образующей всегда можно взять точку ее пересечения с горловым эллипсом
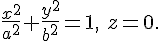
Для такой точки 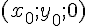
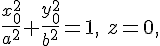
а формулы  и и  принимают вид принимают вид
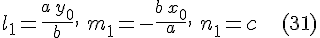
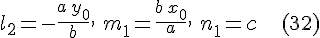
Разобьем множество образующих на два семейства: к первому семейству отнесем образующие
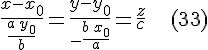
ко второму
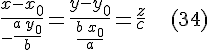
где 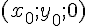 --- координаты точки горлового эллипса. --- координаты точки горлового эллипса.
ТЕОРЕМА 8.2. Две прямолинейные образующие однополостного гиперболоида  , принадлежащие к разным семействам, всегда лежат в одной плоскости и параллельны в том и только в том случае, когда они проходят через диаметрально противоположные точки горлового эллипса. , принадлежащие к разным семействам, всегда лежат в одной плоскости и параллельны в том и только в том случае, когда они проходят через диаметрально противоположные точки горлового эллипса.
Доказательство. Пусть  и и  --- произвольные точки горлового эллипса, а --- произвольные точки горлового эллипса, а
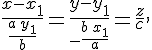

проходящие через них образующие разных семейств.
Применяя необходимое и достаточное условие принадлежности двух прямых одной плоскости, будем иметь
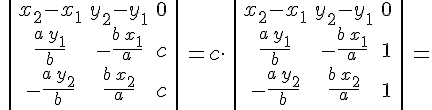
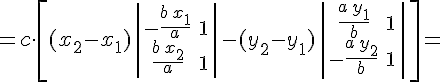
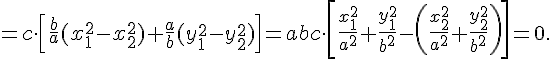
Итак, доказано, что любые две прямолинейные образующие однополостного гиперболоида, принадлежащие разным семействам, лежат в одной плоскости, т.е. либо пересекаются, либо параллельны. Данные образующие параллельны в том и только в том случае, если координаты их направляющих векторов пропорциональны, т.е. если выполняются равенства
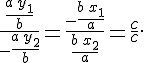
Откуда следуют равенства
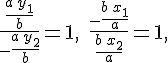
а, значит,
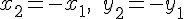
Теорема доказана полностью.
ТЕОРЕМА 8.3. Две прямолинейные образующие однополостного гиперболоида, принадлежащие одному семейству, скрещиваются.
Доказательство. Пусть  и и  --- различные точки горлового эллипса, а --- различные точки горлового эллипса, а
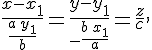
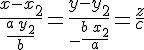
проходящие через них различные образующие одного семейства.
Имеем
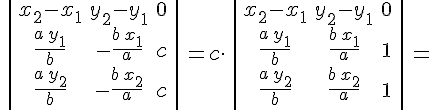

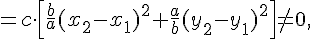
так как  и хотя бы одно из чисел и хотя бы одно из чисел  отлично от нуля. отлично от нуля.
Точно так же можно убедиться в том, что скрещиваются две любые образующие другого семейства. Теорема доказана.
Из теорем 8.1 и 8.3 следует, что через каждую точку однополостного гиперболоида проходят две образующие, принадлежащие разным семействам. Отсюда следует, что однополостный гиперболоид есть геометрической место точек, принадлежащих всем прямолинейным образующим одного семейства.
ТЕОРЕМА 8.4. Никакие три прямолинейные образующие однополостного гиперболоида, принадлежащие одному семейству, не параллельны одной плоскости.
Доказательство. Рассмотрим направляющие векторы
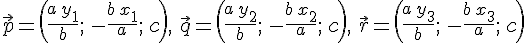
трех образующих одного семейства.
Имеем
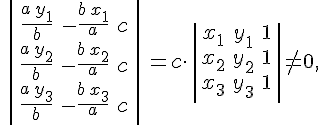
так как точки  --- точки горлового эллипса, которые не лежат на одной прямой. --- точки горлового эллипса, которые не лежат на одной прямой.
Таким образом, направляющие векторы рассматриваемых образующих некомпланарны. Теорема доказана.
Не нашли, что искали? Воспользуйтесь поиском по сайту:
©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|


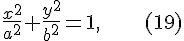
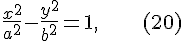
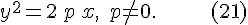
 ,
,  ,
,  , направляющими линиями являются соответственно эллипс
, направляющими линиями являются соответственно эллипс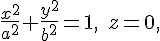

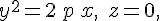
 .
. --- произвольная точка однополостного гиперболоида
--- произвольная точка однополостного гиперболоида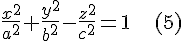
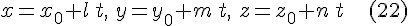
 и прямой
и прямой  , подставим в уравнение
, подставим в уравнение  и
и  их выражения из формул
их выражения из формул 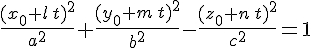
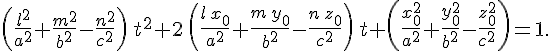
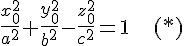
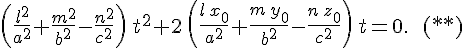
 удовлетворялось при всех значениях
удовлетворялось при всех значениях  , а это возможно тогда и только тогда, когда оба коэффициента при
, а это возможно тогда и только тогда, когда оба коэффициента при  и
и 
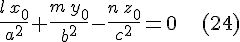
 направляющего вектора прямой
направляющего вектора прямой  следует, что
следует, что  , так как в противном случае
, так как в противном случае  мы имели бы также
мы имели бы также  , что противоречит определению направляющего вектора прямой линии. Так как направляющий вектор прямой определяется с точностью до коллинеарности и по доказанному
, что противоречит определению направляющего вектора прямой линии. Так как направляющий вектор прямой определяется с точностью до коллинеарности и по доказанному  . Тогда система уравнений
. Тогда система уравнений  примет вид
примет вид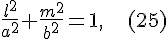

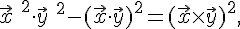
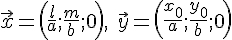
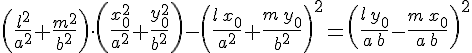
 ,
, 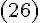 и
и 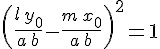
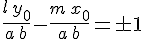
 и
и  направляющего вектора
направляющего вектора  прямолинейных образующих однополостного гиперболоида
прямолинейных образующих однополостного гиперболоида 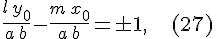
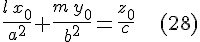
 , знак
, знак  , получим первое решение этой системы, которое вместе с равенством
, получим первое решение этой системы, которое вместе с равенством 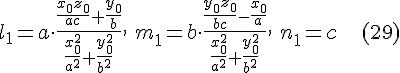
 , получим второе решение этой системы, которое вместе с равенством
, получим второе решение этой системы, которое вместе с равенством 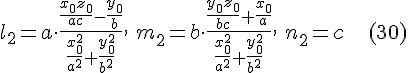
 и
и  прямолинейных образующих однополостного гиперболоида
прямолинейных образующих однополостного гиперболоида 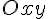 в точке, лежащей на горловом эллипсе. Поэтому за начальную точку каждой образующей всегда можно взять точку ее пересечения с горловым эллипсом
в точке, лежащей на горловом эллипсе. Поэтому за начальную точку каждой образующей всегда можно взять точку ее пересечения с горловым эллипсом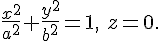
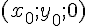
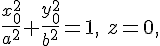
 и
и  принимают вид
принимают вид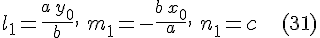
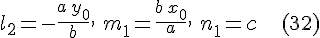
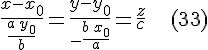
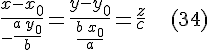
 и
и  --- произвольные точки горлового эллипса, а
--- произвольные точки горлового эллипса, а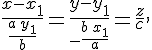

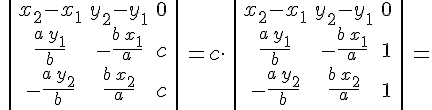
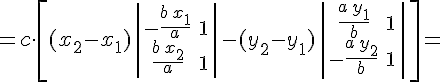
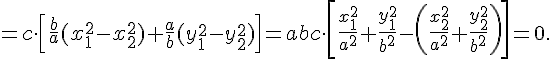
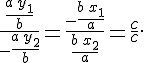
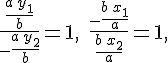
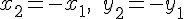
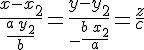
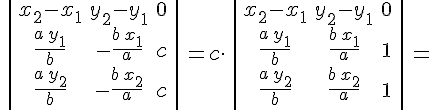

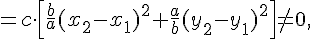
 и хотя бы одно из чисел
и хотя бы одно из чисел  отлично от нуля.
отлично от нуля.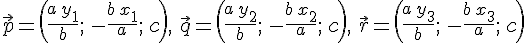
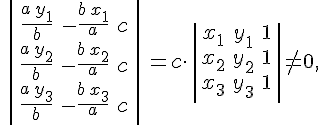
 --- точки горлового эллипса, которые не лежат на одной прямой.
--- точки горлового эллипса, которые не лежат на одной прямой.