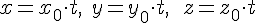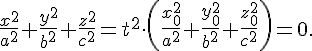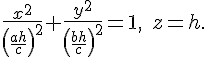Эллиптический параболоид.
Определение 4.1. Эллиптическим параболоидом называется поверхность, уравнение которой в некоторой специально выбранной прямоугольной системе координат, имеет вид
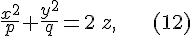
где  . .
Будем считать, что  . Если . Если  , то эллиптический параболоид , то эллиптический параболоид  --- это параболоид вращения, так как получается вращением параболы --- это параболоид вращения, так как получается вращением параболы
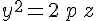
вокруг оси  , являющейся осью этой параболы. , являющейся осью этой параболы.
Ось  является осью симметрии эллиптического параболоида является осью симметрии эллиптического параболоида  , а плоскости , а плоскости  и и  --- его плоскостями симметрии. Начало координат для эллиптического параболоида --- его плоскостями симметрии. Начало координат для эллиптического параболоида  является точкой пересечения этой поверхности с ее осью является точкой пересечения этой поверхности с ее осью  и называется вершиной. и называется вершиной.
Рассмотрим сечения эллиптического параболоида  плоскостями плоскостями  , параллельными плоскости , параллельными плоскости 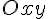 . Нетрудно видеть, что произвольная такая плоскость пересекает эллиптический параболоид . Нетрудно видеть, что произвольная такая плоскость пересекает эллиптический параболоид  по линии по линии
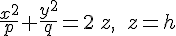
или
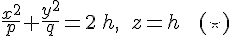
Если  , то первое уравнение , то первое уравнение  не имеет действительных решений, так как не имеет действительных решений, так как  . Это означает, что плоскость . Это означает, что плоскость  при при  не пересекает эллиптический параболоид не пересекает эллиптический параболоид  . Другими словами, эллиптический параболоид . Другими словами, эллиптический параболоид  лежит в неотрицательном полупространстве относительно плоскости лежит в неотрицательном полупространстве относительно плоскости  . .
Если  , то первое уравнение , то первое уравнение  имеет единственное решение имеет единственное решение  , т.е. плоскость , т.е. плоскость 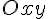 имеет с эллиптическим параболоидом только одну общую точку имеет с эллиптическим параболоидом только одну общую точку  --- вершину. --- вершину.
Если  , то, переписав уравнения , то, переписав уравнения  в виде в виде
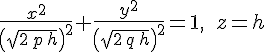
видим, что сечением является эллипс с центром в точке 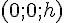 , оси которого параллельны прямым , оси которого параллельны прямым 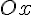 и и  , а полуоси равны , а полуоси равны
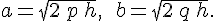
Заметим, что полуоси увеличиваются по мере удаления плоскости сечения от координатной плоскости  . .
Плоскость  пересекает эллиптический параболоид пересекает эллиптический параболоид  по параболе по параболе
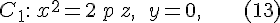
а плоскость  --- по параболе --- по параболе
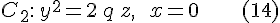
Таким образом, числа 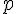 и и  --- параметры парабол --- параметры парабол  , ,  , получающихся в сечении параболоида его плоскостями симметрии (эти параболы называются главными сечениями). , получающихся в сечении параболоида его плоскостями симметрии (эти параболы называются главными сечениями).
Рассмотрим теперь сечения эллиптического параболоида  плоскостями, параллельными плоскости плоскостями, параллельными плоскости  , т.е. плоскостями, выраженными уравнением , т.е. плоскостями, выраженными уравнением  . Уравнения линии сечения: . Уравнения линии сечения:

или
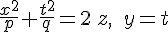
или
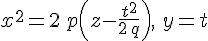
Эти уравнения выражают параболу с вершиной в точке  , ось, которой выражается уравнениями , ось, которой выражается уравнениями  и одинаково направленной с осью и одинаково направленной с осью  . Параметр этой параболы равен . Параметр этой параболы равен 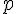 , т.е. параметру главного сечения , т.е. параметру главного сечения  эллиптического параболоида. эллиптического параболоида.
Таким образом, эллиптический параболоид может быть образован параллельным переносом параболы  , при котором вершина параболы , при котором вершина параболы  перемещается по параболе перемещается по параболе  ; плоскость параболы ; плоскость параболы  перпендикулярна плоскости параболы перпендикулярна плоскости параболы  , а оси этих парабол параллельны и одинаково направлены. , а оси этих парабол параллельны и одинаково направлены.
Аналогичная картина получается и для сечений эллиптического параболоида  плоскостями, параллельными плоскости плоскостями, параллельными плоскости  . .
5 Гиперболический параболоид.
Определение 5.1. Гиперболическим параболоидом называется поверхность, уравнение которой в некоторой специально выбранной прямоугольной системе координат, имеет вид
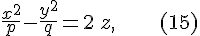
где  . .
Для гиперболического параболоида  плоскости плоскости  и и  являются плоскостями симметрии, а ось являются плоскостями симметрии, а ось  --- осью симметрии. Ось симметрии гиперболического параболоида называется просто его осью. Точка, в которой ось гиперболического параболоида пересекает эту поверхность, называется вершиной. Гиперболический параболоид --- осью симметрии. Ось симметрии гиперболического параболоида называется просто его осью. Точка, в которой ось гиперболического параболоида пересекает эту поверхность, называется вершиной. Гиперболический параболоид  имеет вершину в начале координат. имеет вершину в начале координат.
Плоскости  и и  , являющиеся для гиперболического параболоида , являющиеся для гиперболического параболоида  плоскостями симметрии, называются главными плоскостями гиперболического параболоида. плоскостями симметрии, называются главными плоскостями гиперболического параболоида.
Гиперболический параболоид
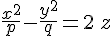
в случае  имеет только одну ось симметрии (ось имеет только одну ось симметрии (ось  ), если же ), если же  , то параболоид имеет еще две оси симметрии: , то параболоид имеет еще две оси симметрии:
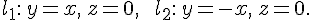
В самом деле, если координаты точки  удовлетворяют уравнению удовлетворяют уравнению
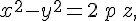
то этому же уравнению удовлетворяют координаты точки  , симметричной с точкой , симметричной с точкой  относительно прямой относительно прямой  . Так же доказывается, что прямая . Так же доказывается, что прямая  является осью симметрии. является осью симметрии.
Плоскость  пересекает гиперболический параболоид пересекает гиперболический параболоид  по линии, определяемой уравнениями по линии, определяемой уравнениями
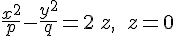
или

которая является совокупностью двух прямых линий:
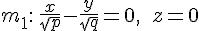
и
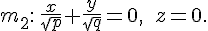
Плоскость  , параллельная плоскости , параллельная плоскости 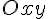 , пересекает гиперболический параболоид , пересекает гиперболический параболоид  по линии, определяемой уравнениями: по линии, определяемой уравнениями:
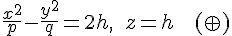
Если  , то эти уравнения можно переписать в виде , то эти уравнения можно переписать в виде
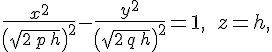
которые определяют гиперболу, расположенную в плоскости  с центром в точке с центром в точке 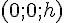 , действительная ось которой параллельна оси , действительная ось которой параллельна оси  , а мнимая --- параллельна оси , а мнимая --- параллельна оси  . .
Если  , то уравнения , то уравнения  линии сечения можно представить в виде линии сечения можно представить в виде

которые определяют гиперболу, расположенную в плоскости  с центром в точке с центром в точке 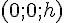 , действительная ось которой параллельна оси , действительная ось которой параллельна оси  , а мнимая --- параллельна оси , а мнимая --- параллельна оси 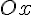 . .
Плоскость  пересекает гиперболический параболоид пересекает гиперболический параболоид  по параболе по параболе
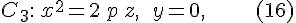
а плоскость  --- по параболе --- по параболе
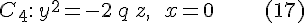
Таким образом, числа 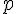 и и  --- параметры парабол --- параметры парабол  , ,  , получающихся в сечении параболоида его плоскостями симметрии (эти параболы называются главными сечениями). , получающихся в сечении параболоида его плоскостями симметрии (эти параболы называются главными сечениями).
Рассмотрим теперь сечения гиперболического параболоида  плоскостями, параллельными плоскости плоскостями, параллельными плоскости  , т.е. плоскостями, выраженными уравнением , т.е. плоскостями, выраженными уравнением  . Уравнения линии сечения: . Уравнения линии сечения:
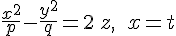
или
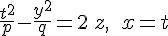
или
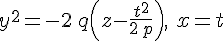
Эти уравнения выражают параболу с вершиной в точке  , ось, которой выражается уравнениями , ось, которой выражается уравнениями  и противоположно направленной с осью и противоположно направленной с осью  . Параметр этой параболы равен . Параметр этой параболы равен  , т.е. параметру главного сечения , т.е. параметру главного сечения  гиперболического параболоида. гиперболического параболоида.
Таким образом, гиперболический параболоид может быть образован параллельным переносом параболы  , при котором вершина параболы , при котором вершина параболы  перемещается по параболе перемещается по параболе  ; плоскость параболы ; плоскость параболы  перпендикулярна плоскости параболы перпендикулярна плоскости параболы  , а оси этих парабол параллельны и противоположно направлены. , а оси этих парабол параллельны и противоположно направлены.
Аналогичная картина получается и для сечений гиперболического параболоида  плоскостями, параллельными плоскости плоскостями, параллельными плоскости  . .
Рассмотренные сечения дают представление о форме гиперболического параболоида
Конус второго порядка.
Определение 6.1. Конусом второго порядка называется поверхность, уравнение которой в некоторой специально выбранной прямоугольной системе координат, имеет вид
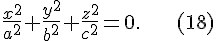
Будем считать, что  . Начало координат является центром симметрии . Начало координат является центром симметрии  и называется вершиной конуса; оси координат являются осями симметрии (главные оси); координатные плоскости являются плоскостями симметрии (главные плоскости). Осью конуса и называется вершиной конуса; оси координат являются осями симметрии (главные оси); координатные плоскости являются плоскостями симметрии (главные плоскости). Осью конуса  называют обычно ось называют обычно ось  . .
Докажем основное свойство конуса:
ТЕОРЕМА 6.1. Если на конусе  лежит точка лежит точка  (не совпадающая с вершиной (не совпадающая с вершиной  ), то на нем лежат все точки прямой ), то на нем лежат все точки прямой  , проходящей через вершину , проходящей через вершину  и эту точку и эту точку  . .
Доказательство. В самом деле, если  --- произвольная точка, лежащая на прямой --- произвольная точка, лежащая на прямой  , то , то
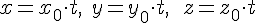
и потому
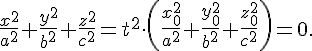
Таким образом, поверхность  образована прямыми, проходящими через начало координат. Поэтому для представления вида этой поверхности достаточно рассмотреть ее сечение какой-нибудь плоскостью образована прямыми, проходящими через начало координат. Поэтому для представления вида этой поверхности достаточно рассмотреть ее сечение какой-нибудь плоскостью  , параллельной плоскости , параллельной плоскости  . В сечении получится эллипс, уравнения которого . В сечении получится эллипс, уравнения которого
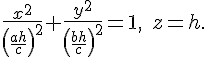
Центр этого эллипса лежит на оси  в точке в точке 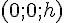 , его оси параллельны координатным осям , его оси параллельны координатным осям 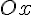 и и  . .
Следовательно, поверхность  образована прямыми, соединяющими начало координат со всеми точками этого эллипса. образована прямыми, соединяющими начало координат со всеми точками этого эллипса.
Не нашли, что искали? Воспользуйтесь поиском по сайту:
©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|


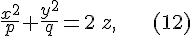
 .
. . Если
. Если  , то эллиптический параболоид
, то эллиптический параболоид  --- это параболоид вращения, так как получается вращением параболы
--- это параболоид вращения, так как получается вращением параболы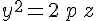
 , являющейся осью этой параболы.
, являющейся осью этой параболы. и
и  --- его плоскостями симметрии. Начало координат для эллиптического параболоида
--- его плоскостями симметрии. Начало координат для эллиптического параболоида  , параллельными плоскости
, параллельными плоскости 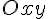 . Нетрудно видеть, что произвольная такая плоскость пересекает эллиптический параболоид
. Нетрудно видеть, что произвольная такая плоскость пересекает эллиптический параболоид 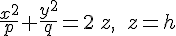
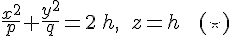
 , то первое уравнение
, то первое уравнение  не имеет действительных решений, так как
не имеет действительных решений, так как  . Это означает, что плоскость
. Это означает, что плоскость  .
. , то первое уравнение
, то первое уравнение  , т.е. плоскость
, т.е. плоскость  --- вершину.
--- вершину. , то, переписав уравнения
, то, переписав уравнения 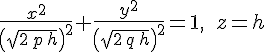
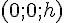 , оси которого параллельны прямым
, оси которого параллельны прямым 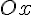 и
и  , а полуоси равны
, а полуоси равны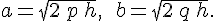
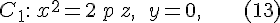
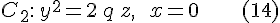
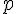 и
и  --- параметры парабол
--- параметры парабол  ,
,  , получающихся в сечении параболоида его плоскостями симметрии (эти параболы называются главными сечениями).
, получающихся в сечении параболоида его плоскостями симметрии (эти параболы называются главными сечениями). . Уравнения линии сечения:
. Уравнения линии сечения:
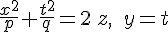
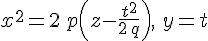
 , ось, которой выражается уравнениями
, ось, которой выражается уравнениями  и одинаково направленной с осью
и одинаково направленной с осью 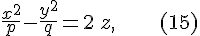
 плоскости
плоскости 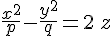
 имеет только одну ось симметрии (ось
имеет только одну ось симметрии (ось 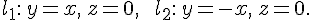
 удовлетворяют уравнению
удовлетворяют уравнению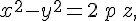
 , симметричной с точкой
, симметричной с точкой  относительно прямой
относительно прямой  . Так же доказывается, что прямая
. Так же доказывается, что прямая  является осью симметрии.
является осью симметрии. пересекает гиперболический параболоид
пересекает гиперболический параболоид 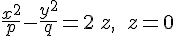

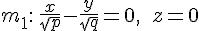
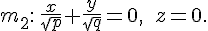
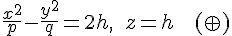
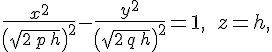
 линии сечения можно представить в виде
линии сечения можно представить в виде
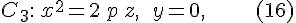
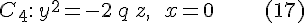
 ,
,  , получающихся в сечении параболоида его плоскостями симметрии (эти параболы называются главными сечениями).
, получающихся в сечении параболоида его плоскостями симметрии (эти параболы называются главными сечениями). . Уравнения линии сечения:
. Уравнения линии сечения: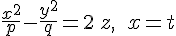
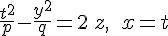
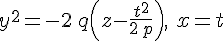
 , ось, которой выражается уравнениями
, ось, которой выражается уравнениями  и противоположно направленной с осью
и противоположно направленной с осью 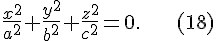
 . Начало координат является центром симметрии
. Начало координат является центром симметрии  и называется вершиной конуса; оси координат являются осями симметрии (главные оси); координатные плоскости являются плоскостями симметрии (главные плоскости). Осью конуса
и называется вершиной конуса; оси координат являются осями симметрии (главные оси); координатные плоскости являются плоскостями симметрии (главные плоскости). Осью конуса  (не совпадающая с вершиной
(не совпадающая с вершиной  ), то на нем лежат все точки прямой
), то на нем лежат все точки прямой  , проходящей через вершину
, проходящей через вершину  .
.