|
|
При прямолинейном перемещенииЕсли при действии постоянной силы
где В системе СИ работа выражается в джоулях: 1 Дж = 1 H∙м, килоджоулях: 1 кДж = 103 Дж, или в мегаджоулях: 1 МДж = 106 Дж. Из формулы (10.1) видно, что работа – величина алгебраическая.
Рис. 10.1. Работа силы
1. При изменении угла 2. При изменении угла 3. Заметим, что при Рассмотренные выше три частных случая значений работы силы при
где
а б в
Рис. 10.2. Работа силы тяжести:
10.2. Работа равнодействующей силы
Если на точку действует одновременно несколько сил, то алгебраическая сумма их работ равна работе равнодействующей силы. Допустим, что перемещение точки
Сложив правые и левые части этих равенств, получим
Известно, что сумма проекций сил на некоторую ось равна проекции равнодействующей этих сил на ту же ось:
Таким образом,
Рис. 10.3. Работа равнодействующей силы
Так как
то
или в общем случае для любого числа сил:
При равномерном прямолинейном движении точки приложенная к ней система сил уравновешена (первая аксиома динамики), т. е.
(алгебраическая сумма работ уравновешенной системы сил, приложенных к точке, равна нулю). 10.3. Работа переменной силы на криволинейном пути
Чтобы определить работу непостоянной силы F при перемещении точки М по криволинейной траектории
а б
Рис. 10.4. Работа переменной силы при перемещении по криволинейной траектории
Просуммировав все элементарные работы переменной силы
Разложив силу
Интегралы могут быть определены лишь в том случае, если известен закон движения точки.
10.4. Мощность
Скалярная величина
характеризующая быстроту совершения работы, называется средней мощностью силы. В СИ мощность выражается в ваттах:
Если в течение некоторого времени t мощность машины остается постоянной или меняется несущественно, то произведенная работа выражается формулой
отсюда и появляется единица времени 1 кВт · ч = 103 Вт · 3600 c =
10.5. Механический коэффициент полезного действия
В технике работа сил обычно связана с преодолением различных сопротивлений, для выполнения этой работы создается множество разнообразных машин и механизмов. Силы сопротивления – полезное сопротивление Fпс, для преодоления которого машины или механизмы и предназначены; – вредное сопротивление Fвс, которое приходится вынужденно преодолевать попутно с полезным. Тогда вся работа, которую совершает машина или механизм:
где
Отношение полезной работы ко всей совершенной работе называется механическим коэффициентом полезного действия:
В технике распространены случаи работы машин при их последовательном соединении друг с другом. Допустим, имеется совокупность трех механизмов с КПД
Рис. 10.5. Последовательное соединение машин Вывод: чем длиннее «цепочка» совместно работающих механизмов, тем меньше её общий КПД, причем общий КПД всегда меньше самого низкого из числа перемножаемых КПД.
10.6. Работа сил на наклонной плоскости
Пусть требуется поднять на высоту h груз, сила тяжести которого G (рис. 10.6).
Рис. 10.6. Работа силы при поднятии груза
Предположим, что подъем осуществляется тремя способами: – вертикально; – по наклонной плоскости с углом подъема α; – по менее крутой плоскости с углом подъема β (β < α). Если считать, что груз перемещается равномерно, то работа при подъеме груза во всех трех случаях совершается одинаковая:
Но в первом случае приходится преодолевать силу тяжести G, во втором – Так как β < α, то Наклонная плоскость как одно из средств получения выигрыша в силе при перемещении тяжести широко используется в технике.
Если сила F направлена параллельно наклонной плоскости (рис. 10.7), то при перемещении вверх по наклонной плоскости тела на него кроме силы F действуют еще три силы: – сила тяжести G, нормальная реакция наклонной плоскости Rn, значение которой
– сила трения Rf, значение которой
Рис. 10.7. Работа силы на наклонной плоскости
При равномерном подъеме тела М четыре силы образуют уравновешенную систему. Алгебраическая сумма работ этих сил равна нулю:
где
Если же требуется определить значение силы F, то с учетом того, что
Полезную часть работы сил F составляет работа по подъему тела на высоту
Таким образом, КПД наклонной плоскости при подъеме груза силой направленной параллельно наклонной плоскости:
Вывод: КПД наклонной плоскости зависит только от угла ее наклона и коэффициента трения при перемещении груза по плоскости.
10.7. Работа и мощность при вращательном движении тел
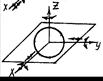
Допустим, что к рукоятке C колеса, насаженного на ось OZ, приложена сила
Рис. 10.8. Вектор силы при вращательном движении тела Но так как
При повороте колеса на угол
Если при этом вращающий момент
(работа при вращении тела равна произведению вращающего момента на угол поворота). Разделив обе части этого равенства на
или, так как
(мощность при вращении тела равна произведению вращающего момента на угловую скорость). Из формулы (10.3) вытекает важное следствие:
(при постоянной мощности вращающий момент обратно пропорционален угловой скорости).
10.8. Трение качения. Работа при качении тел
Трением качения называется сопротивление, возникающее при перекатывании одного тела по поверхности другого. Тело 1 и каток 2 (рис. 10.9) абсолютно недеформируемые. Малая сила F вместе с силой трения
Рис. 10.9. Работа сил при качении тела
На самом деле абсолютно недеформируемых тел нет (рис. 10.9, б). При перекатывании катка силой При качении катка на него действуют четыре силы, образующие две пары сил: движущую пару (
Для перекатывания катка сила
Глава 11. Общие теоремы динамики
11.1. Импульс силы. Количество движения. Кинетическая энергия
Любое взаимодействие тел, приводящее к какому-либо изменению движения, длится некоторое время. Векторная мера действия силы
Векторная мера механического движения точки Скалярная мера механического движения точки
11.2. Теорема об изменении количества движения точки
Пусть на точку массой m действует система постоянных сил, равнодействующая которых
(изменение количества движения точки равно импульсу всех сил). Спроецировав на оси координат обе части векторного равенства (11.1), в общем случае получим: а) систему трех скалярных уравнений:
где б) если силы, действующие на точку, лежат в одной плоскости, то получим два скалярных уравнения; в) если силы действуют вдоль одной прямой, то, спроецировав уравнение (11.1) на эту прямую, получим одно скалярное уравнение:
11.3. Теорема об изменении кинетической энергии точки
Пусть на точку действует система постоянных сил, равнодействующая которых
На прямолинейном пути
Отсюда с учетом того, что
т. е. изменение кинетической энергии точки равно сумме работ действующих сил.
11.4. Понятие о механической системе
Совокупность материальных точек, связанных между собой силами взаимодействия, называется механической системой (рис. 11.1). Например, механическую систему образуют Земля и Луна или спортивный самолет и буксируемый им планер. Любое материальное тело рассматривается в механике как механическая система, образуемая совокупностью материальных точек. Абсолютно твердое тело носит название неизменяемой механической системы, так как расстояние между материальными точками остается неизменным. Изменяемые системы – любые машины или механизмы.
Рис. 11.1. К понятию о механической системе
Если рассматривать какую-либо механическую систему, то силы, действующие на точки системы со стороны точек или тел, не входящих в эту систему, называются внешними (Fe, Re), а силы, действующие на точки системы со стороны точек или тел этой же системы, называются внутренними (Fi). Главный вектор всех внутренних сил механической системы равен нулю, причем это условие соблюдается, только если рассматриваемая механическая система неизменяемая. Движение механической системы зависит: 1) от действующих сил; 2) суммарной массы системы
где m – масса механической системы;
3) положения центра масс системы. Движение центра масс определяется (только при поступательном движении) уравнением
где m – масса системы;
Как видим, это уравнение аналогично основному уравнению динамики точки. Смысл его состоит в том, что центр масс системы движется как материальная точка, в которой сосредоточена масса всей системы и приложены все внешние силы.
11.5. Основное уравнение динамики вращающегося тела
Пусть твердое тело (рис. 11.2) под действием внешних сил
Рис. 11.2. К определению работы сил, действующих на вращающееся тело
Алгебраическая сумма моментов всех сил (активных сил и сил сопротивления) относительно оси OZ
называется вращающим моментом. Рассматривая твердое тело как механическую систему, разобьем его на множество материальных точек массами Приложим к каждой материальной точке элементарные силы инерции: касательную
(моменты сил У любой точки вращающегося тела числовое значение касательного ускорения
Величина Основное уравнение динамики вращающегося тела:
В СИ момент инерции тела выражается в кг · м2. 11.6. Кинетическая энергия тела. Кинетический момент
Кинетическая энергия тела складывается из кинетических энергий его отдельных точек. 1. При поступательном движении тела (рис. 11.3) скорости всех его точек равны между собой и равны
где m – масса тела;
Рис. 11.3. К определению кинетической энергии при поступательном движении тела
2. При вращательном движении тела с некоторой угловой скоростью
Рис. 11.4. К определению кинетической энергии при вращательном движении тела
А так как
Кинетическая энергия тела при сложном его движении (в частности, при плоскопараллельном) складывается из кинетической энергии поступательного движения со скоростью центра масс и кинетической энергии вращательного движения с угловой скоростью вокруг оси, проходящей через центр масс, т. е.
Кроме кинетической энергии мерой вращательного движения тела является величина РАЗДЕЛ 2 ОСНОВЫ ПОСТРОЕНИЯ И ИССЛЕДОВАНИЯ МЕХАНИЗМОВ
Глава 12. Структура механизмов
12.1. Основные понятия
Механизмомназывается система тел, предназначенная для преобразования движения одного или нескольких твердых тел в требуемые движения других твердых тел. Машинойназывается устройство, выполняющее механические движения для преобразования энергии, материалов и информации с целью замены или облегчения физического и умственного труда человека. В зависимости от основного назначения различают энергетические, технологические, транспортные и информационные машины. Энергетические машины предназначены для преобразования энергии. К ним относятся, например, электродвигатели, двигатели внутреннего сгорания, турбины, электрогенераторы. Технологические машины предназначены для преобразования обрабатываемого предмета, которое состоит в изменении его размеров, форм, свойств или состояния. Транспортные машины предназначены для перемещения людей и грузов. Информационные машины предназначены для получения и преобразования информации. В состав машины обычно входят различные механизмы. Всякий механизм состоит из отдельных твердых тел, называемых деталями. Детальявляется такой частью машины, которую изготовляют без сборочных операций. Детали могут быть простыми (гайка, шпонка и т. п.) и сложными (коленчатый вал, корпус редуктора, станина станка и т. п.). Детали частично или полностью объединяют в узлы. Узел представляет собой законченную сборочную единицу, состоящую из ряда деталей, имеющих общее функциональное назначение (подшипник, муфта, редуктор и т. п.). Сложные узлы могут включать в себя несколько узлов (подузлов), например, в состав редуктора входят подшипники, валы с насаженными на них зубчатыми колесами и т. п. Одно или несколько жестко соединенных твердых тел, входящих в состав механизма, называются звеном. В каждом механизме имеется стойка, т. е. звено неподвижное или принимаемое за неподвижное. Из подвижных звеньев выделяют входные и выходные. Входным называется звено, которому сообщается движение, преобразуемое механизмом в требуемые движения других звеньев. Выходным звеном называется звено, совершающее движение, для выполнения которого предназначен механизм. Кинематической парой называется соединение двух соприкасающихся звеньев, допускающее их относительное движение.
12.2. Классификация кинематических пар. Кинематические цепи
По числу связей, наложенных кинематической парой на относительное движение ее звеньев, все кинематические пары делятся на пять классов. Свободное тело (звено) в пространстве обладает шестью степенями свободы.
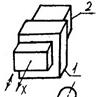
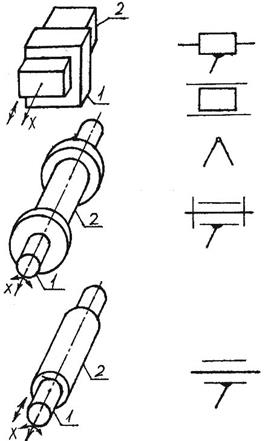
Основные кинематические пары
Поверхности, линии и точки, по которым соприкасаются звенья, называются элементами кинематической пары. Различают низшие (1–5) пары, элементами которых являются поверхности, и высшие (6, 7) пары, элементами которых могут быть только линии или точки. Кинематические цепи Кинематической цепью называется система звеньев, связанных между собой кинематическими парами (рис. 12.1, 12.2).
12.3. Структурный синтез и анализ механизмов
Структурный синтез механизма заключается в проектировании его структурной схемы, под которой понимается схема механизма, указывающая стойку, подвижные звенья, виды кинематических пар и их взаимное расположение. Метод структурного синтеза механизмов, предложенный русским ученым Л.В. Ассуром в 1914 г., состоит в следующем: механизм может быть образован путем наслоения структурных групп к одному или нескольким начальным звеньям и стойке. Структурной группой (группой Ассура) называется кинематическая цепь, число степеней свободы которой равно нулю после присоединения ее внешними кинематическими парами к стойке и которая не распадается на более простые цепи, удовлетворяющие этому условию. Принцип наслоения иллюстрируется на примере образования Для структурных групп плоских механизмов с низшими парами
откуда
где W –число степеней свободы; n – число подвижных звеньев; Рн – число низших пар. Этому соотношению удовлетворяют следующие сочетания.
В роли одноподвижных пар выступают низшие пары. Простейшей является структурная группа, у которой n = 2 и Pн = 3. Она называется структурной группой второго класса.
а б в г
Рис. 12.3. Принцип наслоения структур, φ1 –угол поворота кривошипа (обобщенная координата)
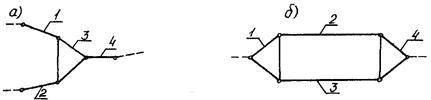
Порядок структурной группы определяется числом элементов ее внешних кинематических пар, которыми она может присоединяться к механизму. Все группы второго класса имеют второй порядок. Структурные группы, у которых n = 4 и Рн = 6, могут быть третьего или четвертого класса (рис. 12.4).
а б Рис. 12.4. Структурные группы: а – третьего класса; б – четвертого класса Класс структурной группы в общем случае определяется числом кинематических пар в замкнутом контуре, образованном внутренними кинематическими парами. Класс механизма определяется высшим классом структурной группы, входящей в его состав. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|
на точку М (рис. 10.1) ее перемещение 
, то скалярная мера действия силы называется работой: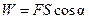
, (10.1)
– угол между направлением действия силы и направлением перемещения.
значение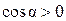 
. Поэтому если угол 
положительная. В частном случае, когда направление действия силы совпадает с направлением перемещений ( 
и 
.
. Следовательно, если угол 
и 
.
и 
, т. е. работа силы, направленной перпендикулярно перемещению точки, равна нулю.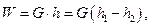
– начальная высота точки над заданным уровнем на Земле;
– конечная высота над тем же уровнем.
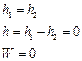
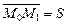произошло при действии на нее трех сил: 
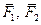и 
(рис. 10.3). Тогда, обозначив работу каждой из сил соответственно W1, W2 и W3, можем записать: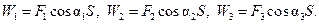
и есть работа равнодействующей силы
,
.
, и тогда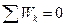
, надо дугу 
, настолько малых, что каждую из них можно считать отрезком прямой (рис. 10.4, а). Тогда работа силы F на перемещении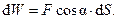 
(10.2)
и 
, направленные соответственно по нормали и касательной, увидим, что работа нормальной составляющей равняется нулю и, следовательно, в формуле (10.2) произведение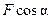 
выражает модуль касательной составляющей силы 
, и этой формуле можно придать вид
,
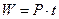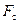, которые преодолевает любая машина (механизм):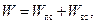
– работа по преодолении полезного сопротивления, отсюда
(рис. 10.5). Если работа, совершенная механизмами,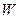 
и их полезная работа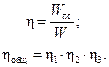 
, в третьем – 
.
, значит, 
– работа силы тяжести;
– работа силы трения;
– работа нормальной реакции.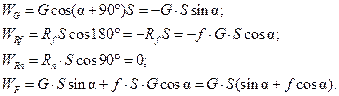
, получаем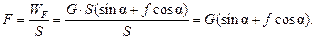
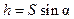и тогда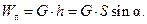
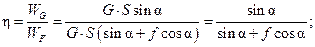
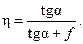
(рис. 10.8). При вращении колеса точка приложения силы 
.
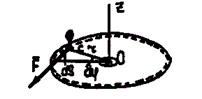
, то 
, где произведение 
называется вращающим моментом. Следовательно, при вращении тела элементарная работа
работа
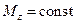, то
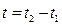(время действия вращающего момента), получим его мощность:
(10.3)
, приложенной к катку в точке K, образуют пару (F , 
опорной поверхности также смещается несколько вперед на длину 
относительно теоретической точки касания K и отклоняется от нормали 
на небольшой угол (рис. 10.9, в).
) с моментом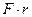 
и пару сопротивления качению ( 
, 
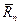) с моментом 
. Момент пары сопротивления иначе называют моментом трения качения, а величину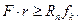 
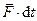, равная произведению силы на элементарный промежуток времени ее действия, называется элементарным импульсом силы. Направление вектора импульса совпадает с направлением вектора силы. Единица импульса в СИ – Н ∙ с: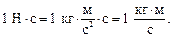
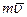, равная произведению массы точки на ее скорость в данный момент времени, называется количеством движения. Направление вектора количества движения совпадает с направлением вектора скорости. Единица количества движения в СИ – 
. Как видим, единицы импульса силы и количества движения одинаковы.
, равная половине произведения массы точки на квадрат ее скорости, называется кинетической энергией. Единица кинетической энергии – джоуль (Дж):
согласно основному закону динамики
.
;
.
,
,
,
– массы ее отдельных точек;
,
– результирующая всех внешних сил, приложенных к точкам системы;
– ускорение центра масс системы.
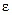(эти силы на рис. 11.2 не показаны) вращается около оси OZ с угловым ускорением 
.
, с ускорением 
, которое разложим на касательное 
и нормальное 
ускорение.
и нормальную 
. Согласно принципу Даламбера, активные силы, силы реакции связей и силы инерции образуют уравновешенную систему. Поэтому алгебраическая сумма моментов всех этих сил относительно оси OZ должна быть равна нулю, т. е.
относительно оси OZ равны нулю, так как линии действия этих сил пересекают ось).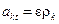
, поэтому значение 
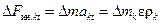, где 
, равная сумме произведений масс всех точек тела на квадраты их расстояний от оси вращения, называется моментом инерции тела (системы) относительно этой оси.
– скорости центра масс тела. Поэтому легко понять, что кинетическая энергия тела при поступательном движении
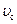– значение скорости центра масс.
(рис. 11.4) все его точки движутся по окружностям различных радиусов 
. Определив кинетическую энергию каждой точки 
и сложив ее по всему объему тела, получим
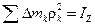– момент инерции тела относительно оси Z, для кинетической энергии находим такое выражение:
, называемая кинетическим моментом вращающегося тела. Кинетический момент в СИ выражается в 
.
