|
|
РЕШЕНИЕ СИСТЕМ НЕЛИНЕЙНЫХ УРАВНЕНИЙСистема нелинейных уравнений с р неизвестными обычно имеет вид
fi (x1, .... хр) = 0, i=1, .... р,
где хотя бы одна функция fi нелинейная. Для решения такой системы в редких случаях можно применить метод последовательного исключения неизвестных, который приводит решение системы к решению одного нелинейного уравнения с одним неизвестным с последующей подстановкой. Например, для решения нелинейной системы
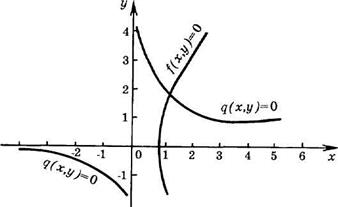
x y2 +4 = 0, x - y2 +5 = 0
из второго уравнения найдем х = у2 — 5 и подставим в первое, получим уравнение с одним неизвестным: у2(у2 - 5) + 4 = 0, корни которого y1 = 1, у2 = - 1, y3 =2, y4 = -2. Следовательно, решениями системы являются точки
A (-4, 1), В(- 4, -1), С( -1, 2), D( - 1, -2).
Однако в подавляющем большинстве случаев нелинейные системы решают итерационными методами.
Метод простой итерации
Метод простой итерации применим к системам, которые предварительно приведены к виду x1 = φ1 (x1, .... хр) …………………………………………. (6.1) xp = φp (x1, .... хр) или, в векторной форме, х = Ф(х). (6.2) Пусть x(0) = (x1(0), .... хр(0) ) начальное приближение. Последующие приближения в методе простой итерации находятся по формулам
x1(m+)1 = φ1 (x1(m), .... хр(m) ), x1(m+1) = φ1 (x1(m), .... хр(m) ,), (6.3) ……………….…. x1(m+1) = φ1 (x1(m), .... хр(m) ),
или, в векторной форме, х(m+1)= Ф(х(m) .(6.4)
Если последовательность векторов х(т) = (x1(m), .... хр(m) ) сходится к вектору x* = (x1*, ..., хp*), а функции φi (x) непрерывны, то вектор х* является решением системы (6.2). Для получения условий сходимости метода итераций введем в р-мерном векторном пространстве какую-либо норму (например, кубическую, октаэдрическую или сферическую). Теорема 3. Пусть для уравнения (6.2) и начального приближения х(0) выполнены условия: 1) для ||х-х(0)|| ≤ δ (6.5) вектор-функция Ф удовлетворяет условию ||Ф (х')-Ф (х")|| ≤ q ||х'-х"||, (6.6) где 0 < q < 1; 2) ||Ф (х(0)) – х0|| ≤ (1 – q) δ , Тогда уравнение (6.2) в сфере (6.5) имеет единственное решение х*, к нему сходится последовательность (6.4) и погрешность метода оценивается неравенством ||х(m)-х*|| ≤ Сходимость метода итераций считается хорошей, если q ≤ 1/2 Приведем достаточное условие, обеспечивающее выполнение неравенства (6.6) в кубической норме. Сфера (6.5) в кубической норме является р-мерным кубом с центром в точке x(0) = (x1(0), ..., х(р0)): ||х-х(0)|| =
Предположим, что в кубе (6.8) функции φi ( i = 1, ..., р ) имеют непрерывные частные производные
Пример. Методом простой итерации найти решение системы
f1 (x, y) = 2x – sin 0,5 (x - y) = 0, f2 (x, y) = 2y – cos 0,5 (x + y) = 0,
с точностью ε = 10 -2. Решение. Графически отделяем корни системы. Из рис. 5.1 видно, что корень единственный и расположен в квадрате |х| ≤ 0,5, |у — 0,5| ≤ 0,5.
Рис. 6.1
Преобразуем данную систему к виду
х = 0,5 sin 0,5 (х - y) ≡ φ1 (х, у), y = 0,5 cos 0,5 (х + y) ≡ φ2 (х, у).
Убеждаемся, что неравенство (6.9) выполнено q ≤ 0,5. За начальное приближение возьмем хо = 0, уо = = 0,5. Дальнейшие вычисления отражены в табл. 6.1.
Таблица 6.1
Метод Ньютона
Метод Ньютона применяется к решению систем уравнений вида
fi(х1..., хр) = 0, I = l , ..., р, (6.10) или, в векторной форме, F(x) = 0. (6.11)
Введем матрицу Якоби J(х) для функций fi(х), I = l, ..., р, которые будем предполагать непрерывно дифференцируемыми:
J(x) = ……………………………
Пусть задано начальное приближение х(0). Вместо нелинейного уравнения (6.11) решаем линейное уравнение F(x(0)) – J(х(0)) (х-х(0)) = 0.(6.13)
Если det J (х(0)) ≠ 0, то уравнение (6.13) имеет единственное решение, которое обозначим х(1). Здесь удобно решать уравнение (6.13) относительно
F(x(m)) – J(х(m)) (х-х(m)) = 0.
которая в координатной форме имеет вид
f1(х(m)) + (6.14) fp(х(m)) + Для системы второго порядка f (x, y) = 0, g (x, y) = 0
последовательные приближения по методу Ньютона вычисляются по формулам
xn+1 = xn -
f {хп, уп) fy '(хп, уп) Аn = g(xn, yл) gy'(xn, yn) ,
Bn = gx'(xn, yn) g(xn, yл) ,
fx '(хп, уп)fy '(хп, уп) Jn = ≠ 0. gx'(xn, yn) gy'(xn, yn) Метод Ньютона сходится, если начальное приближение выбрано удачно и матрица J(х*) невырожденна. На практике итерации обычно оканчивают, если ||x(n+1)- х(n)|| ≤ ε. Для выбора начального приближения применяют графический метод, метод проб, метод табулирования и т. д.
Рис. 6.2 Пример. Найти решение системы f (x, y) = х 3 - у2 – 1 = 0, g (x, y) = ху3 - у - 4 = 0 методом Ньютона с точностью ε =10-3.
Матрица Якоби имеет вид 3 х2 - 2у J(x,y)= . у3 3x у2 - 1
Дальнейшие вычисления отражены в табл. 6.2. Таблица 6.2
ОСНОВНАЯ ЛИТЕРАТУРА
1. Березин И.С., Жидков Н.П. Методы вычислений. - М.: Госиздат, 1962.- 639с. 2. Быховцев В.Е., Быховцев А.В., Бондарева В.В. Компьютерное моделирование систем нелинейной механики грунтов. -Гомель: УО «ГГУ им. Ф. Скорины», 2002.-215с. 3. Демидович Б.П., Марон И.А. Основы вычислительной математики. М.:Наука, 1970. 4. Копченова Н.В., Марон И.А. Вычислительная математика в примерах и за дачах. - М.:Наука, 1972. 5. Крылов В.И.,Бобков В.В., Монастырный П.И. Выислительные методы. - М.: Наука, 1977.- 399с. 6. Икрамов Х.Д. Численные методы для симметричных линейных систем (прямые методы). - М.: Наука, 1988.- 160с. 7. Фаддеев А.К., Фаддеева В.Н. Вычислительные методы линейной алгебры.- М.: Госиздат, 1960.- 656с.
ДОПОЛНИТЕЛЬНАЯ ЛИТЕРАТУРА
1. Вергасов В.А. и др. Вычислительная математика. -М.: Недра, 1976.- 230с. 2. Воеводин В.В. Численные методы алгебры. Теория и алгорифмы.- М.:Наука, 1966. 3. Самарский А.А. Введение в численные методы. - М.:Наука, 1982.

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
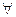 х', х" из сферы
х', х" из сферы ||Ф (х(0)) – х0|| . (6.7)
||Ф (х(0)) – х0|| . (6.7) . (6.8)
. (6.8) φi /
φi / 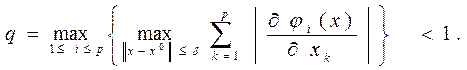 (6.9)
(6.9)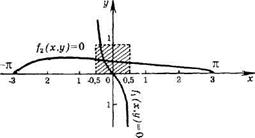





 х(0) = х - х(0), а затем вычислять x(l) = x(0) +
х(0) = х - х(0), а затем вычислять x(l) = x(0) + 

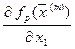

 , yn+1 = yn -
, yn+1 = yn -  ,
,