Методы решения СЛАУ с трехдиагональной матрицей
Методы обращения матриц
Задача нахождения обратной матрицы вплотную примыкает к задаче решения систем линейных алгебраических уравнений вида  . Пусть . Пусть  - обратная матрица к матрице - обратная матрица к матрице  . Умножим обе части последнего матричного уравнения слева на матрицу . Умножим обе части последнего матричного уравнения слева на матрицу  . В результате получим . В результате получим  . Откуда . Откуда  или или  . Таким образом, зная обратную матрицу . Таким образом, зная обратную матрицу  , можно определить решение системы уравнений. , можно определить решение системы уравнений.
a) Метод Гаусса.
Используем метод Гаусса для нахождения обратной матрицы. Пусть обратная матрица  к матрице к матрице
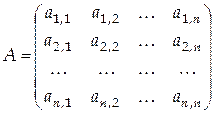 имеет вид имеет вид  . .
Из определения обратной матрицы следует, что  , т. е. , т. е.
 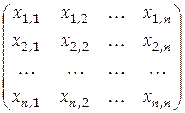 = =  . .
Перемножая матрицы в левой части равенства и сравнивая с соответствующими элементами матрицы  в правой части, получим в правой части, получим  систем линейных алгебраических уравнений с систем линейных алгебраических уравнений с  неизвестными вида неизвестными вида
 , ,
где вектор   -ой системы имеет вид: -ой системы имеет вид:  , ,  , если , если  . Решив все . Решив все  систем методом Гаусса, получим матрицу систем методом Гаусса, получим матрицу  . .
b) Метод Жордана.
Пусть после  -го шага преобразования по методу Жордана матрица -го шага преобразования по методу Жордана матрица  имеет вид имеет вид
 . .
Разделим  - ю строку матрицы - ю строку матрицы  на ведущий элемент на ведущий элемент  и исключим все внедиагональные элементы и исключим все внедиагональные элементы  - го столбца. После выполнения этой операции приходим к матрице - го столбца. После выполнения этой операции приходим к матрице 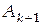 , которая имеет точно такой же вид, что и предыдущая матрица , которая имеет точно такой же вид, что и предыдущая матрица  , но с заменой индекса , но с заменой индекса  на индекс на индекс  . Матрицы . Матрицы  и и 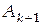 связаны соотношением связаны соотношением  , где матрица , где матрица  имеет вид имеет вид
 . .
Применяя описанный процесс к матрице  , получим матрицы , получим матрицы  , причем, , причем,  , ,
 , ,
…………………..
 , ,
 . .
Но в соответствии с методом Жордана  . Отсюда находим . Отсюда находим
 . .
Из определения обратной матрицы имеем 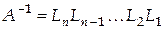
Обозначим  . Матрица . Матрица  выражается следующим образом выражается следующим образом  , т. е. переход от матрицы , т. е. переход от матрицы  к матрице к матрице  осуществляется по тем же формулам, что и переход от матрицы осуществляется по тем же формулам, что и переход от матрицы  к матрице к матрице 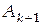 . Кроме того, первые . Кроме того, первые  столбцов матрицы столбцов матрицы  и последние и последние  столбцов матрицы столбцов матрицы  совпадают со столбцами единичной матрицы. Это позволяет определять элементы обратной матрицы внутри одного массива. Таким образом, метод Жордана дает простой алгоритм вычисления обратной матрицы без использования дополнительной оперативной памяти. Пусть совпадают со столбцами единичной матрицы. Это позволяет определять элементы обратной матрицы внутри одного массива. Таким образом, метод Жордана дает простой алгоритм вычисления обратной матрицы без использования дополнительной оперативной памяти. Пусть  . Строим последовательно матрицы . Строим последовательно матрицы  , вычисляя их коэффициенты , вычисляя их коэффициенты  по следующим формулам по следующим формулам
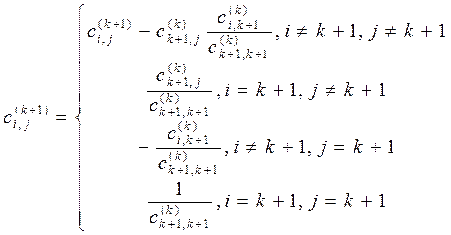
Тогда  . При этом все вычисления происходят внутри одного массива. . При этом все вычисления происходят внутри одного массива.
с) Метод отражений.
Метод отражений позволяет преобразовать произвольную невырожденную матрицу в верхнюю треугольную с помощью матриц отражения  следующим образом следующим образом 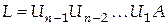 . Тогда после умножения слева на матрицу . Тогда после умножения слева на матрицу  получим, что получим, что  . Из последнего равенства следует, что . Из последнего равенства следует, что  . Так как матрица . Так как матрица  верхняя треугольная, то и матрица верхняя треугольная, то и матрица  будет верхней треугольной и, значит, может быть легко определена. будет верхней треугольной и, значит, может быть легко определена.
Рассмотрим алгоритм обращения верхней треугольной матрицы. Пусть
 , ,  . .
Тогда  и по правилу умножения матриц получаем и по правилу умножения матриц получаем
 , ,  ; ;
 , , 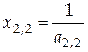 , ,  ; ;
 , ,  , ,  , ,
 ; ;
………………………………………………………………………………………………………
 , ,  , ,  , ,
 . .
ЛЕКЦИЯ № 14
4.9. Обусловленность систем линейных алгебраических уравнений
Математическая задача поставлена корректно, если ее решение существует и единственно и если оно непрерывно зависит от входных данных. Последнее свойство задачи называется устойчивостью относительно входных данных.
Рассмотрим вопрос корректности решения системы линейных алгебраических уравнений (4.1) (  ) с квадратной матрицей порядка ) с квадратной матрицей порядка  . Решение этой системы существует для любого . Решение этой системы существует для любого  - мерного вектора - мерного вектора  тогда и только тогда, когда тогда и только тогда, когда  . В этом случае можно определить обратную матрицу . В этом случае можно определить обратную матрицу  , обратную матрице , обратную матрице  , и записать решение в виде , и записать решение в виде  . .
Входными данными для системы линейных алгебраических уравнений являются правая часть  и элементы и элементы  , ,  , матрицы , матрицы  . Поэтому различают устойчивость по правой части (когда возмущается только правая часть . Поэтому различают устойчивость по правой части (когда возмущается только правая часть  , а матрица , а матрица  остается неизменной) и коэффициентную устойчивость (когда возмущается только матрица остается неизменной) и коэффициентную устойчивость (когда возмущается только матрица  , а правая часть , а правая часть  остается неизменной). остается неизменной).
Будем считать, что решение и правая часть системы (4.1) принадлежат линейному пространству  , состоящему из , состоящему из  - мерных векторов. Введем в пространстве - мерных векторов. Введем в пространстве  норму. Нормой вектора называется действительное число, удовлетворяющее условиям: норму. Нормой вектора называется действительное число, удовлетворяющее условиям:
 для любого для любого  , ,  ; ;
 для любого числа для любого числа  и любого и любого  ; ;
 для любых для любых  . .
Нормой матрицы  , подчиненной данной норме вектора, называется число , подчиненной данной норме вектора, называется число
 . (4.32) . (4.32)
Из определения следует, что  для всех для всех  , ,  , ,
 для любых матриц для любых матриц  , ,  ; ; 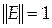 , где , где  - единичная матрица. - единичная матрица.
Вместе с основной системой (4.1) рассмотрим возмущенную систему
 , (4.33) , (4.33)
которая отличается от (4.1) правой частью. Будем предполагать, что матрица  не возмущается. Обозначим не возмущается. Обозначим  , ,  . .
Говорят, что система (4.1) устойчива по правой части, если при любых  и и  справедлива оценка справедлива оценка
 , (4.34) , (4.34)
где  - постоянная, не зависящая от правых частей - постоянная, не зависящая от правых частей  и и  . Оценка (4) выражает факт непрерывной зависимости решения от правой части, т. е. показывает, что . Оценка (4) выражает факт непрерывной зависимости решения от правой части, т. е. показывает, что  при при  . Вопрос исследования устойчивости является важным потому, что никогда нельзя задать правую часть . Вопрос исследования устойчивости является важным потому, что никогда нельзя задать правую часть  точно. На самом деле вместо вектора точно. На самом деле вместо вектора  задается какой-то близкий ему вектор задается какой-то близкий ему вектор  . Погрешность . Погрешность  может возникнуть, например, в результате округления. может возникнуть, например, в результате округления.
Покажем, что если  , то система (4.1) устойчива по правой части. Так как из (4.1) и (4.33) следует, что , то система (4.1) устойчива по правой части. Так как из (4.1) и (4.33) следует, что  , то в силу существования обратной матрицы , то в силу существования обратной матрицы  и и
 , (4.35) , (4.35)
т.е. выполняется неравенство (4.34) с константой  . .
Замечание. Чем ближе к нулю определитель матрицы  , тем больше постоянная , тем больше постоянная  и, следовательно, тем сильнее погрешность правой части может исказить искомое решение. и, следовательно, тем сильнее погрешность правой части может исказить искомое решение.
В оценку (4.35) входят абсолютные погрешности решения  и правой части и правой части  . При решении системы (4.1) более естественными характеристиками являются относительные погрешности . При решении системы (4.1) более естественными характеристиками являются относительные погрешности
 , ,  . .
Получим оценку, выражающую относительную погрешность решения через относительную погрешность правой части. Для этого используем неравенство
 , (4.36) , (4.36)
которое следует из (4.1). Перемножив (4.35) и (4.36), получим оценку
 , (4.37) , (4.37)
где  . .
Число  называется числом обусловленности матрицы называется числом обусловленности матрицы  , которое характеризует степень зависимости относительной погрешности решения от относительной погрешности правой части. Матрицы с большим числом обусловленности , которое характеризует степень зависимости относительной погрешности решения от относительной погрешности правой части. Матрицы с большим числом обусловленности  называются плохо обусловленными матрицами. При численном решении систем с плохо обусловленными матрицами возможно сильное накопление погрешностей. называются плохо обусловленными матрицами. При численном решении систем с плохо обусловленными матрицами возможно сильное накопление погрешностей.
Предположим, что в системе (4.1) возмущены как правая часть, так и коэффициенты матрицы  . Рассмотрим вместе с системой (4.1) возмущенную систему . Рассмотрим вместе с системой (4.1) возмущенную систему
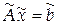 (4.38) (4.38)
и обозначим  , ,  , ,  . .
Лемма 4.1. Пусть  - квадратная матрица, удовлетворяющая условию - квадратная матрица, удовлетворяющая условию  и и  - единичная матрица. Тогда существует матрица - единичная матрица. Тогда существует матрица  , причем , причем
 . (4.39) . (4.39)
Доказательство: Для любого вектора  имеем имеем
 , ,
где  . Однородное уравнение . Однородное уравнение  имеет только нулевое имеет только нулевое
решение, так как из равенства  и неравенства и неравенства  следует, следует,
что  и и  . Поэтому в неравенстве . Поэтому в неравенстве  можно обозначить можно обозначить
 , ,  и переписать его в виде и переписать его в виде  . Отсюда получаем . Отсюда получаем
 , ,
следовательно, из определения нормы матрицы, подчиненной данной норме вектора, получаем утверждение (4.39).
Теорема 4.4. Пусть матрица  имеет обратную и пусть выполнено условие имеет обратную и пусть выполнено условие
 . (4.40) . (4.40)
Тогда матрица  имеет обратную и справедлива следующая оценка относительной погрешности: имеет обратную и справедлива следующая оценка относительной погрешности:
 . (4.41) . (4.41)
Доказательство: Докажем, что существует матрица, обратная матрице  . Имеем . Имеем
 , ,
где  . По условию (10) имеем . По условию (10) имеем
 , (4.42) , (4.42)
поэтому согласно лемме 4.1 существует матрица  , следовательно, и , следовательно, и  . .
Получим оценку (4.41). Для этого сначала представим вектор  в виде в виде
 . .
Согласно (4.1) имеем  , поэтому , поэтому
 . (4.43) . (4.43)
Получим оценки норм матриц  и и  . Обозначим . Обозначим  . Имеем . Имеем
 , ,
 , ,  . .
По лемме 4.1 получим
 , ,
так как  . Далее, . Далее,

и
 . .
Переходя к равенству (4.43), получим
 . .
Преобразуем  . Получаем . Получаем
 . .
Тогда окончательно имеем неравенство
 , ,
которое совпадает с неравенством (4.41).
Число обусловленности  зависит от того, какая норма матриц выбрана, но при любой норме зависит от того, какая норма матриц выбрана, но при любой норме  . Чем больше это число, тем хуже обусловленность системы. Обычно . Чем больше это число, тем хуже обусловленность системы. Обычно  уже означает плохую обусловленность. В практических расчетах таким определением плохой обусловленности пользуются редко, так как для проверки необходимо находить обратную матрицу, что при плохо обусловленной матрице уже означает плохую обусловленность. В практических расчетах таким определением плохой обусловленности пользуются редко, так как для проверки необходимо находить обратную матрицу, что при плохо обусловленной матрице  нелегко сделать. Чаще ограничиваются проверкой условия нелегко сделать. Чаще ограничиваются проверкой условия  , хотя оно является необходимым, но недостаточным. , хотя оно является необходимым, но недостаточным.
ЛЕКЦИЯ № 15
Методы решения СЛАУ с трехдиагональной матрицей
Не нашли, что искали? Воспользуйтесь поиском по сайту:
©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|


 . Пусть
. Пусть  - обратная матрица к матрице
- обратная матрица к матрице  . Умножим обе части последнего матричного уравнения слева на матрицу
. Умножим обе части последнего матричного уравнения слева на матрицу  . Откуда
. Откуда  или
или  . Таким образом, зная обратную матрицу
. Таким образом, зная обратную матрицу 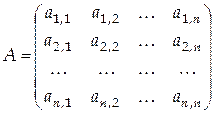 имеет вид
имеет вид  .
. , т. е.
, т. е.
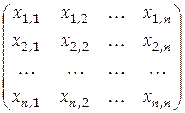 =
=  .
. в правой части, получим
в правой части, получим  систем линейных алгебраических уравнений с
систем линейных алгебраических уравнений с  ,
,
 -ой системы имеет вид:
-ой системы имеет вид:  ,
,  , если
, если  . Решив все
. Решив все  -го шага преобразования по методу Жордана матрица
-го шага преобразования по методу Жордана матрица  имеет вид
имеет вид .
. - ю строку матрицы
- ю строку матрицы  и исключим все внедиагональные элементы
и исключим все внедиагональные элементы 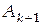 , которая имеет точно такой же вид, что и предыдущая матрица
, которая имеет точно такой же вид, что и предыдущая матрица  . Матрицы
. Матрицы  , где матрица
, где матрица  имеет вид
имеет вид .
. , получим матрицы
, получим матрицы  , причем,
, причем,  ,
, ,
, ,
, .
. . Отсюда находим
. Отсюда находим .
.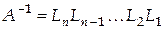
 . Матрица
. Матрица  выражается следующим образом
выражается следующим образом  , т. е. переход от матрицы
, т. е. переход от матрицы  к матрице
к матрице  столбцов матрицы
столбцов матрицы  . Строим последовательно матрицы
. Строим последовательно матрицы  , вычисляя их коэффициенты
, вычисляя их коэффициенты  по следующим формулам
по следующим формулам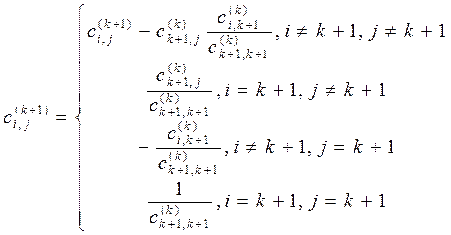
 . При этом все вычисления происходят внутри одного массива.
. При этом все вычисления происходят внутри одного массива. следующим образом
следующим образом 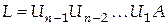 . Тогда после умножения слева на матрицу
. Тогда после умножения слева на матрицу  получим, что
получим, что  . Из последнего равенства следует, что
. Из последнего равенства следует, что  . Так как матрица
. Так как матрица  верхняя треугольная, то и матрица
верхняя треугольная, то и матрица  ,
,  .
. и по правилу умножения матриц получаем
и по правилу умножения матриц получаем ,
,  ;
; ,
, 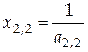 ,
,  ;
; ,
,  ,
,  ,
, ;
; ,
,  ,
,  ,
, .
. . В этом случае можно определить обратную матрицу
. В этом случае можно определить обратную матрицу  ,
,  , матрицы
, матрицы  , состоящему из
, состоящему из  для любого
для любого  ,
,  ;
; для любого числа
для любого числа  и любого
и любого  ;
; для любых
для любых  .
. . (4.32)
. (4.32) для всех
для всех  ,
, для любых матриц
для любых матриц  ;
; 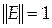 , где
, где  , (4.33)
, (4.33) ,
,  .
. справедлива оценка
справедлива оценка , (4.34)
, (4.34) - постоянная, не зависящая от правых частей
- постоянная, не зависящая от правых частей  при
при  . Вопрос исследования устойчивости является важным потому, что никогда нельзя задать правую часть
. Вопрос исследования устойчивости является важным потому, что никогда нельзя задать правую часть  , то в силу существования обратной матрицы
, то в силу существования обратной матрицы  и
и , (4.35)
, (4.35) .
. и, следовательно, тем сильнее погрешность правой части может исказить искомое решение.
и, следовательно, тем сильнее погрешность правой части может исказить искомое решение. ,
,  .
. , (4.36)
, (4.36) , (4.37)
, (4.37) .
. называется числом обусловленности матрицы
называется числом обусловленности матрицы  . Рассмотрим вместе с системой (4.1) возмущенную систему
. Рассмотрим вместе с системой (4.1) возмущенную систему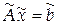 (4.38)
(4.38) ,
,  ,
,  .
. - квадратная матрица, удовлетворяющая условию
- квадратная матрица, удовлетворяющая условию  и
и  , причем
, причем . (4.39)
. (4.39) ,
, . Однородное уравнение
. Однородное уравнение  имеет только нулевое
имеет только нулевое следует,
следует, и
и  . Поэтому в неравенстве
. Поэтому в неравенстве  ,
,  и переписать его в виде
и переписать его в виде  . Отсюда получаем
. Отсюда получаем ,
, . (4.40)
. (4.40) имеет обратную и справедлива следующая оценка относительной погрешности:
имеет обратную и справедлива следующая оценка относительной погрешности: . (4.41)
. (4.41) . Имеем
. Имеем ,
, . По условию (10) имеем
. По условию (10) имеем , (4.42)
, (4.42) .
. .
. , поэтому
, поэтому . (4.43)
. (4.43) и
и  . Имеем
. Имеем ,
, .
. ,
, . Далее,
. Далее,
 .
. .
. . Получаем
. Получаем .
. ,
, . Чем больше это число, тем хуже обусловленность системы. Обычно
. Чем больше это число, тем хуже обусловленность системы. Обычно  уже означает плохую обусловленность. В практических расчетах таким определением плохой обусловленности пользуются редко, так как для проверки необходимо находить обратную матрицу, что при плохо обусловленной матрице
уже означает плохую обусловленность. В практических расчетах таким определением плохой обусловленности пользуются редко, так как для проверки необходимо находить обратную матрицу, что при плохо обусловленной матрице  , хотя оно является необходимым, но недостаточным.
, хотя оно является необходимым, но недостаточным.