
|
|
Рассмотрим систему трехточечных уравнений
и предположим, что коэффициенты
Системы вида (4.44) возникают при трехточечной аппроксимации краевых задач для обыкновенных дифференциальных уравнений второго порядка с постоянными и переменными коэффициентами, а также при реализации разностных схем для уравнений в частных производных. Эффективным методом решения системы (4.44) является метод исключения Гаусса, который приводит к формулам прогонки. Предположим, что
с неопределенными коэффициентами
Подставим
Получим
Подставим теперь (4.45) в (4.46) и преобразуем полученное равенство
Последнее уравнение справедливо для любых
Отсюда получаем рекуррентную формулу для
и рекуррентную формулу для определения
В обоих случаях предполагается, что Если коэффициенты
Сравнивая эти уравнения, получим
Используем теперь для определения значения
решая которую находим
Описанный метод решения систем линейных алгебраических уравнений с трехдиагональной матрицей называется методом правой прогонки. Коэффициенты Алгоритм метода правой прогонки будет корректен, если в формулах (4.47) и (4.48) отличны от нуля значения Теорема 4.5 (достаточное условие корректности и устойчивости метода прогонки). Пусть коэффициенты системы (4.1) удовлетворяют условиям
причем хотя бы в одном из неравенств (4.51) или (4.52) выполняется строгое неравенство, т. е. Матрица системы (4.44) имеет диагональное преобладание. Тогда для метода прогонки имеют место неравенства Доказательство: Покажем, что из неравенства
Пусть
Следовательно,
Так как
Покажем, что метод прогонки при выполнении условий теоремы не приводит к накоплению ошибок округления. Пусть
Это означает, что погрешность вычислений не возрастает в процессе решения системы (4.44), т. е. метод прогонки устойчив.
ЛЕКЦИЯ № 16
5. ПОЛНАЯ И ЧАСТИЧНАЯ ПРОБЛЕМЫ СОБСТВЕННЫХ ЗНАЧЕНИЙ. Постановка задачи
В предыдущем материале мы рассмотрели одну из основных групп вычислительных задач линейной алгебры — задачи численного нахождения решения системы линейных алгебраических уравнений. Сейчас рассмотрим другую важную группу таких задач, порождаемую так называемой проблемой собственных значений. Собственным значением (или характеристическим числом) квадратной матрицы А называется такое число λ, что для некоторого ненулевого вектора х имеет место равенство Ах= λ х. (5.0)
Любой ненулевой вектор х, удовлетворяющий этому равенству, называется собственным вектором матрицы А, соответствующим (или принадлежащим) собственному значению λ. Очевидно, что все собственные векторы матрицы определены с точностью до числового множителя. Анализ собственных значений матриц является важной темой научно-технических исследований. Условием существования у однородной системы (5.0) ненулевого решения (для наглядности запишем эту систему в виде (А— λ Е)х = 0является требование
|А- λ Е| =
Это уравнение обычно называют вековым (или характеристическим) уравнением матрицы А. Такие уравнения часто встречаются в приложениях. Левая часть векового уравнения |А- λ Е| = (-1)n (λn – p1 λn-1- p2 λn-2 - …., - рп)
носит название характеристического полинома матрицы А. Старший коэффициент этого полинома равен (—1)п. Иногда вместо характеристического полинома рассматривают полином, отличающийся от характеристического множителем (-1)п. Этот полином Р( λ )= λn – p1 λn-1- p2 λn-2 - …., - рп
обычно называют собственным многочленом матрицы. Собственные значения матрицы являются корнями собственного многочлена. Совокупность всех собственных значений λ1, λг, .... , λп матрицы А, где каждое собственное значение выписано столько раз, какова его кратность как корня собственного многочлена, называется спектром этой матрицы. Собственными же векторами матрицы А являются нетривиальные решения однородной системы (5.0), в которой вместо λподставлены собственные значения λiматрицы. В том случае, когда для данного собственного значения система (5.0) имеет несколько линейно независимых решений, этому собственному значению принадлежит несколько собственных векторов. Задачу вычисления собственных значений и собственных векторов матрицы А можно разбить на три естественных этапа: 1) строение собственного многочлена Р( λ ) матрицы; 2) решение уравнения Р(λ)=0 и нахождение собственных значений λi (i=1, 2,... , п) матрицы; 3) отыскание нетривиальных решений однородных систем (А- λi Е)х = 0),(i=1,2.. ,n), т. е. нахождение собственных векторов матрицы. Каждый из трех отмеченных этапов решения проблемы собственных значений представляет собой достаточно сложную вычислительную задачу. В самом деле, построение собственного многочлена Р(λ), например, связано с развертыванием определителя
что представляет собой значительные технические трудности. Основное затруднение вызвано тем обстоятельством, что λвходит в каждую строку и в каждый столбец определителя. В общем же случае, как известно из алгебры, коэффициенты pi собственного многочлена Р(λ) представляют собой взятые со знаком (-1)i-1 суммы всех главных миноров (т. е. миноров, симметрично расположенных относительно главной диагонали) порядка i определителя матрицы Л. Число таких миноров для каждого i равно числу сочетаний из п по i. Значит, непосредственное вычисление коэффициентов собственного многочлена Р(λ) квадратной матрицы порядка п связано с вычислением 2n -1 определителей различных порядков. Трудности в непосредственном осуществлении второго и третьего этапов решения проблемы собственных значений, т. е. трудности, связанные с решением алгебраических уравнений высоких степеней, и трудности в нахождении нетривиальных решений систем однородных линейных алгебраических уравнений, также значительны. К настоящему времени создано немало специальных вычислительных приемов, упрощающих численное нахождение собственных значений и собственных векторов матрицы. Все эти методы, как и в случае проблемы численного решения системы линейных алгебраических уравнений, можно разделить на точные и итерационные методы. К первой группе относятся методы, по которым сначала строят собственный многочлен матрицы (т. е. вычисляют его коэффициенты р1, р2, ... , рп), затем, находя его корни, получают собственные значения матрицы и уже по ним находят соответствующие собственные векторы. Методы этой группы получили название точных методов в связи с тем обстоятельством, что в случае точного задания (рациональными числами) элементов матрицы и при точном (по правилам действий над обыкновенными дробями) проведении вычислений такие методы приводят к точным значениям коэффициентов собственного многочлена, а координаты собственных векторов при этом оказываются выраженными через соответствующие собственные значения. В методах второй группы собственные значения матрицы определяются непосредственно, без обращения к собственному многочлену, при этом обычно одновременно вычисляются и соответствующие собственные векторы. Вычислительные схемы таких методов носят итерационный характер. В них используется многократное умножение матрицы на вектор. Схемы этого типа обычно приводят к последовательности векторов, имеющей своим пределом собственный вектор, и к числовой последовательности, предел которой является соответствующим собственным значением. Сам факт сходимости этого процесса и ее скорость определяются величиной отношения модулей различных соседних собственных значений. Как правило, итерационные методы позволяют с достаточной точностью определить лишь первые (наибольшие по модулю, например) собственные значения и соответствующие им собственные векторы. Поэтому методы этой группы чаще всего применяются к решению так называемой частичной проблемы собственных значений, т. е. их чаще используют лишь для отыскания одного или нескольких собственных значений матрицы и соответствующих собственных векторов. Точные же методы позволяют решать также и полную проблему собственных значений, т. е. дают возможность находить все собственные значения матрицы и все принадлежащие им собственные векторы. Полная проблема собственных значений в некоторых случаях может быть решена также и специальными итерационными методами. Эти методы, конечно, более трудоемки, чем точные методы и чем итерационные методы решения частичной проблемы собственных значений. Их практическое использование стало возможным лишь с появлением быстродействующих вычислительных машин. Однако перед точными методами решения полной проблемы собствейных значений итерационные методы имеют одно несомненное преимущество, связанное с возможностью нахождения всех собственных значений без предварительного построения собственного многочлена матрицы. Это особенно важно в связи с тем, что ошибки в вычислении коэффициентов собственного многочлена могут сильно сказываться на точности определения его корней, т. е. на точности нахождения собственных значений исходной матрицы (и соответствующих им собственных векторов). Кроме того, большим достоинством итерационных методов перед точными является простота и единообразие производимых действий, что особенно ценно при использовании быстродействующих вычислительных машин. Полная и частичная проблемы собственных значений сильно различаются как по методам их решения, так и по области приложений. Так как решение полной проблемы собственных значений даже в случае матриц не очень высокого порядка обычно связано с очень большим объемом вычислительного труда, то возможность решения частичной проблемы собственных значений другими методами, минуя вычислительные трудности решения полной проблемы, является очень ценной для практики. Таким образом, задача отыскания собственных значений и собственных векторов матрицы сводится к отысканию коэффициентов характеристического уравнения, определению его корней, и к отысканию нетривиальных решений системы Ах = Х, в которой вместо X рассматривают одно из найденных собственных значений. Наиболее простой метод определения собственных чисел и собственных векторов матрицы основан на методе непосредственного вычисления определителя. Покажем это на конкретном примере. Пример 1. Найти собственные числа и собственные векторы матрицы A методом непосредственного вычисления определителя (ε = 0.5 · 10-3 ).
А = Составим характеристическое уравнение матрицы А, корнями которого являются собственные числа матрицы |А- λ Е| = Непосредственно вычислив определитель третьего порядка, имеем
(2 — λ) (4 — λ)( — 1— λ) —15 — 12 — 9(4 — λ) — 10(2 — λ) — 2( — 1— λ) = 0,
откуда λ 3 — 5 λ 2 — 19 λ + 89 = 0. Полученное уравнение решаем методом Ньютона, предварительно отделив корни. Находим
f(λ ) = λ 3 — 5 λ 2— 19 λ + 89, f'(λ) = 3 λ 2—10 λ —l9, следовательно λ1 =1,2; λ2 = 4,7. Составим таблицу знаков функции f(λ )
Как видно из таблицы, уравнение имеет три действительных корня:
λ1
Выберем для уточнения один из них, например λ2. Уменьшим промежуток [-1,2; 4,7], в котором находится этот корень. Для этого вычислим значения функции f(λ ) в некоторых точках промежутка: f(2) = 39 > 0; f(3) = 14 > 0; f(4)= - 3 < 0. Итак, корень λ2 содержится внутри промежутка [3; 4]. Уточнение корня производим по формуле λn+1 = λn - f(λn) / f / (λn)/
После уточнения имеем λ2 ≈ 3,7621. Для определения двух других собственных чисел решаем квадратное уравнение, полученное при делении многочлена f(λ ) на
λ- 3,7621: λ 2—1б2379 λ — 23,6571 = 0: λ1 ≈ - 4,2841; λ3 ≈ 5,5220.
Для определения собственных векторов, соответствующих найденным собственным значениям, воспользуемся системой линейных уравнений, полученных из равенства (А— λ Е)х = 0. При λ1 ≈ - 4,2841 получим систему
6,2841x1 - x2 + 3x3 = 0, - 2х1 + 8,2841 х2 + 5х3 = 0, Зх1 + 2x2 + 3, 2841x3 = 0.
Решив ее, получим х(1) = с (- 0,597; - 0,746; 1)T.
Аналогично определяются два других собственных вектора. При λ2 = 3,7621 имеем -1,7621x1 - x2 + 3x3 = 0, - 2х1 + 0,2379 х2 + 5х3 = 0, Зх1 + 2x2 -4,7621x3 = 0.
х(2) = с (1; -0,492; 0,423)T. При λ3= 5,5220 имеем -3,522x1 - x2 + 3x3 = 0, - 2х1 + 1,522 х2 + 5х3 = 0,
Зх1 + 2x2 - 6,522x3 = 0. х(3) = с ( - 0,00858; 0,228; 1)T.
Рассмотрим один точный вычислительный метод решения проблемы собственных значений, метод А. Н. Крылова, при этом, если противное не оговорено особо, мы будем иметь в виду лишь матрицы с вещественными элементами. Метод А. Н. Крылова В начале тридцатых годов нашего столетия А. Н. Крыловым был предложен достаточно удобный, метод нахождения собственных значений и собственных векторов матриц. Пусть D(λ) ≡ det(λ E - A) = λn + p1 λn-1 + p2 λn-2 + …., + рп (5.1)
— характеристический полином (с точностью до знака) матрицы А. Согласно тождеству Гамильтона — Кели, матрица А обращает в нуль свой характеристический полином; поэтому An + p1 An-1 +…+ pn E = 0. (5.2) Возьмем теперь произвольный ненулевойвектор y (0) = Умножая обе части равенства (5.2) справа на y(0) получим:
An y(0) + p1 An-1 y(0) +…+ pn y(0) = 0. (5.3) Положим: Ak y(0) = y(k) (k=1, 2, ..., п); (5.4)
тогда равенство (5.3) приобретает вид
y(n) + p1 y(n-1) +…+ pn y(0) = 0. (5.5)
или где y(k) =
Следовательно, векторное равенство (5.5*) эквивалентно системе уравнений
p1 yj (n-1) + p2 yj (n-2) + …., + рп yj(0) = -yj(n)(j = 1. 2. . . ., n),(5.6)
из которой можно определить неизвестные коэффициенты p1, p2,....., рп . Так как на основании формулы (5.4) y(k) =A y (k -1), где (k = 1, 2, . . ., п),
то координаты y1 (к) , y2 (к) , …, yn (к) вектора y(k) последовательно вычисляются по формулам
Таким образом, определение коэффициентов pj характеристического полинома (5.1) методом А. Н. Крылова сводится к решению линейной системы уравнений (5.6), коэффициенты которой вычисляются по формулам (5.7), причем координаты начального вектора y (0) = произвольны. Если система (6) имеет единственное решение, то ее корни р1, р2, ..., рп являются коэффициентами характеристического полинома (5.1). Это решение может быть найдено, например, методом Гаусса. Если система (5.6) не имеет единственного решения, то задача усложняется . В этом случае рекомендуется изменить начальный вектор. Пример. Методом А. Н. Крылова найти характеристический полином матрицы А = Решение. Выберем начальный вектор y (0) = Пользуясь формулами (5.7), определим координаты векторов
y(k) = Ak y(0) , (k=1, 2, ..., п).
y(1) = A y(0) =
y(3) = A y(2) =
Составим систему (6):
которая в нашем случае будет иметь вид
Отсюда 208p1 + 30p2 + p3 + p4 = - 2108, 178p1 + 22p2 +2p3 = - 1704, 192p1 + 18p2 +3p3 = - 1656, 242p1 + 20p2 +4p3 = - 1992.
Решив эту систему, получим: р1 = - 4; р2 = - 40; р3 = - 56; р4 = - 20. Следовательно, det(λ E - A) = λ4 - 4 λ3 - 40 λ2 - 56 λ – 20.
Определение собственных чисел матрицы состоит в решении полученного характеристического уравнения каким – либо из ранее рассмотренных методов. Этим самым поставленная задача решена.
ЛЕКЦИЯ № 17

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 (4.44)
(4.44) и
и  отличны от нуля. Матрица этой системы является трехдиагональной и имеет вид
отличны от нуля. Матрица этой системы является трехдиагональной и имеет вид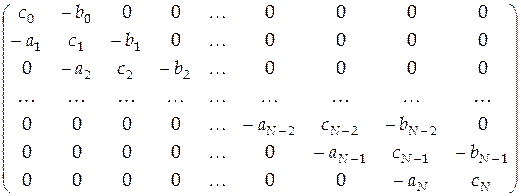
 и
и  связаны рекуррентным соотношением
связаны рекуррентным соотношением (4.45)
(4.45)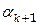 и
и  .
. в уравнение
в уравнение  .
. . После приведения подобных имеем
. После приведения подобных имеем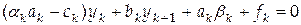 . (4.46)
. (4.46)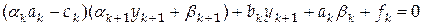 ,
, .
. ,
, .
. ,
, 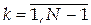 , (4.47)
, (4.47) ,
,  . (4.48)
. (4.48) .
. и
и  известны и известно значение
известны и известно значение  , то, двигаясь от
, то, двигаясь от  к
к  , получим последовательно все
, получим последовательно все  . Имеем
. Имеем ,
, .
. ,
, 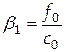 . (4.49)
. (4.49) . В результате получим систему уравнений
. В результате получим систему уравнений ,
, . (4.50)
. (4.50) операций умножения и деления.
операций умножения и деления. . Кроме того, если все
. Кроме того, если все  достаточно велико, то полученное реальное решение будет значительно отличаться от искомого решения.
достаточно велико, то полученное реальное решение будет значительно отличаться от искомого решения. ,
,  ,
,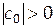 ,
,  ,
, 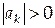 ,
,  ,
,  , (4.51)
, (4.51) ,
, 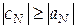 , (4.52)
, (4.52) ,
,  и условий теоремы следует, что
и условий теоремы следует, что  .
. =
=  .
. .
. , то неравенства
, то неравенства  . Если
. Если  , то
, то  и
и  . Значит, если одно из неравенств (4.51) или (4.52) является строгим, то обязательно
. Значит, если одно из неравенств (4.51) или (4.52) является строгим, то обязательно  и
и .
. - искаженное решение, полученное в результате наличия ошибок округления. Тогда из уравнений
- искаженное решение, полученное в результате наличия ошибок округления. Тогда из уравнений следует, что
следует, что , т. е.
, т. е.  , где
, где  и
и . Так как
. Так как  .
.

 (-1)n (λn – p1 λn-1- p2 λn-2 - …., - рп) = (-1)n Р(λ),
(-1)n (λn – p1 λn-1- p2 λn-2 - …., - рп) = (-1)n Р(λ),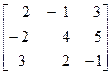
 = 0.
= 0. [- ∞; -1,2]; λ2
[- ∞; -1,2]; λ2 
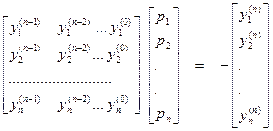 (5.5*)
(5.5*)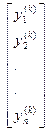 , (k=1, 2, ..., п).
, (k=1, 2, ..., п). ,
,  ,…,
,…,  (5.7)
(5.7)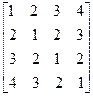
 .
. ; y(2) = A y(1) =
; y(2) = A y(1) =  ;
; ; y(4) = A y(3) =
; y(4) = A y(3) = 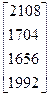 ;
;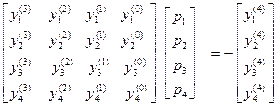

 = -
= -  .
.