
|
|
Взаимное расположение двух прямых на плоскостиЕсли прямые
Условие перпендикулярности этих прямых имеет вид а условие их параллельности Если прямые заданы уравнениями Условие перпендикулярности этих прямых имеет вид Расстояние
Решение типовых задач Пример.Даны вершины треугольника ABC: A(-4;2), B(8;-6), C(2;6). Найти: 1) уравнение стороны AB; 2) уравнение высоты CH; 3) уравнение медианы AM; 4) точку N пересечения медианы AM и высоты CH; 5) уравнение прямой, проходящей через вершину C параллельно стороне AB; 6) расстояние от точки C до прямой AB. Решение. 1) Используем уравнение прямой, проходящей через две точки A и B. Получим уравнение стороны AB: 2) Высота опускается из точки C на сторону AB, угловой коэффициент которой 3) Предварительно найдем координаты середины М отрезка ВС:
4) Точку пересечения N медианы АМ и высоты CH находим из совместного решения им соответствующих уравнений: Решив эту систему, получим 5) Воспользуемся уравнением пучка прямых, проходящих через точку С:
6)Расстояние от точки С до прямой AB вычисляем по формуле
Замечание. Предложенное решение задачи можно считать наиболее оптимальным, так как удачный выбор всевозможных уравнений позволил до минимума сократить количество операций. На практике чаще всего требуется просто решить задачу на основании каких-то данных. Тогда при решении задачи можно использовать только те уравнения, которые Вам известны. Например, воспользуемся уравнением прямой с угловым коэффициентом 1) Найдем уравнение стороны AB, учитывая то, что прямая проходит через две точки. Последнее означает, что координаты точек A и B должны удовлетворять уравнению Подставим значения коэффициентов в уравнение и получим
2) Уравнение высоты CH также ищем в виде Решим систему Уравнение высоты CH запишется в виде 3) Согласно тому, что прямая АМ проходит через две точки, записываем систему равенств: Решив систему, получим Тогда уравнение АМ будет 4) Запишем уравнение прямой, проходящей через точку C, параллельно стороне AB, основываясь снова на уравнении 5) Найдем предварительно точку K пересечения прямых CH и AB из решения системы уравнений Имеем
Линии второго порядка Линией (кривой) второго порядка называется множество точек плоскости, декартовы координаты x и y которых удовлетворяют алгебраическому уравнению второй степени. Окружностью называется множество точек на плоскости, равноудаленных от одной и той же точки, называемой ее центром. Окружность радиусом R с центром в начале координат задается уравнением
Если центр сместить в точку
Эллипсс полуосями a и b симметричный относительно осей координат определяется простейшим (каноническим) уравнением
Точки Число Для любой точки M эллипса сумма расстояний этой точки до фокусов есть величина постоянная, равная 2a: Гиперболас действительной полуосью a, мнимой полуосью b, с центром в начале координат имеет следующее каноническое уравнение:
Фокусы гиперболы – точки Прямые Параболас вершиной в начале координат, симметричная относительно оси Ox, имеет следующее каноническое уравнение: Уравнения вида Кривые эллипс, гипербола и парабола обладают общим свойством: отношение расстояния от любой точки M кривой до фокуса к расстоянию от этой точки до прямой (называемой директрисой) есть величина постоянная
Решение типовых задач Пример. Написать уравнение кривой, модуль разности расстояний от каждой точки которой до точек Решение. Пусть
Упростим это равенство, выполняя следующие операции: Окончательно получим уравнение кривой Пример. Даны точка а) в б) в в) равноудалена от точки Решение: а) Пусть точка
Произведем упрощение полученного равенства:
Следовательно, искомая линия - эллипс. Точка б) Согласно условию задачи
т.е. данная линия – гипербола, для которой точка в) По условию
Получили уравнение параболы с фокусом в точке Пример. Составить канонические уравнения: а) эллипса, расстояние между фокусами которого б) гиперболы с действительной полуосью равной 8 и эксцентриситетом в) параболы, имеющей директрису Решение. а) Каноническое уравнение эллипса имеет вид Значения полуосей эллипса находим из системы уравнений Из первого уравнения имеем б) Каноническое уравнение гиперболы имеет вид На основании предыдущего равенства получим в) В рассматриваемом случае каноническое уравнение параболы должно иметь вид

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 и
и 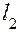 заданы общими уравнениями
заданы общими уравнениями  и
и  , то угол
, то угол 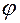 между ними находится из формулы
между ними находится из формулы .
. ,
, .
. и
и  , то угол
, то угол  .
. , а условие иx параллельности
, а условие иx параллельности  .
. от точки
от точки 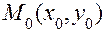 до прямой, заданной в общем виде, вычисляется по формуле
до прямой, заданной в общем виде, вычисляется по формуле  .
. , откуда
, откуда  или
или  .
. . Если обозначим угловой коэффициент стороны CH через
. Если обозначим угловой коэффициент стороны CH через  , то согласно условию перпендикулярности
, то согласно условию перпендикулярности  . Воспользуемся уравнением пучка прямых, проходящих через точку C:
. Воспользуемся уравнением пучка прямых, проходящих через точку C:  . Из этого пучка выберем прямую, перпендикулярную AB, придав значение
. Из этого пучка выберем прямую, перпендикулярную AB, придав значение  . Получим
. Получим  или
или 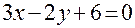 .
.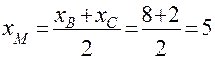 ,
,  . По известным двум точкам составляем уравнение прямой АМ:
. По известным двум точкам составляем уравнение прямой АМ: или
или  .
.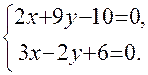
 .
.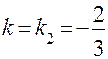 . Получим уравнение искомой прямой в виде
. Получим уравнение искомой прямой в виде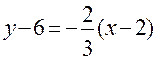 или
или  .
. .
.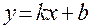 и проследим за тем, как изменяются рассуждения при решении отдельных пунктов задачи.
и проследим за тем, как изменяются рассуждения при решении отдельных пунктов задачи. и
и 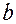 :
:  Решив ее, получим
Решив ее, получим  ,
,  .
. или
или  . Далее учтем, что эта же прямая перпендикулярна AB. Это означает, что
. Далее учтем, что эта же прямая перпендикулярна AB. Это означает, что 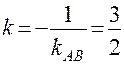 .
. Откуда имеем
Откуда имеем  ,
,  .
. или
или 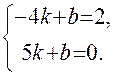
 ,
,  .
. или
или  . Решаем систему уравнений
. Решаем систему уравнений  Имеем
Имеем  . Тогда уравнение искомой прямой будет
. Тогда уравнение искомой прямой будет  или
или  .
.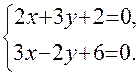
 . Далее находим расстояние от точки C до прямой AB как расстояние между точками C и K:
. Далее находим расстояние от точки C до прямой AB как расстояние между точками C и K: .
. .
. , то уравнение примет вид
, то уравнение примет вид .
. .
. и
и  , расположенные на оси Ox и отстоящие на расстоянии
, расположенные на оси Ox и отстоящие на расстоянии  от начала координат, называются фокусами эллипса. В частном случае, если a=b, то фокусы
от начала координат, называются фокусами эллипса. В частном случае, если a=b, то фокусы 
 называется эксцентриситетом эллипса и является мерой его сплюснутости (при
называется эксцентриситетом эллипса и является мерой его сплюснутости (при  эллипс вырождается в окружность). Прямые
эллипс вырождается в окружность). Прямые 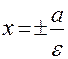 называются директрисами эллипса.
называются директрисами эллипса.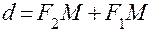 . Это характеристическое свойство эллипса часто принимается за определение эллипса.
. Это характеристическое свойство эллипса часто принимается за определение эллипса. .
.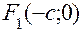 и
и  , где
, где  , а ее эксцентриситет
, а ее эксцентриситет 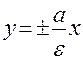 – асимптоты гиперболы, а прямые
– асимптоты гиперболы, а прямые  . Это характеристическое свойство гиперболы часто принимается за определение гиперболы.
. Это характеристическое свойство гиперболы часто принимается за определение гиперболы. , где
, где 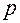 - параметр параболы. При
- параметр параболы. При  ветви параболы направлены вправо, при
ветви параболы направлены вправо, при  – влево. Точка
– влево. Точка  - фокус, а прямая
- фокус, а прямая  – директриса параболы. Парабола представляет собой множество всех точек плоскости, равноотстающих от данной точки (фокуса) и от данной прямой (директрисы). Это характеристическое свойство параболы часто принимается за определение параболы.
– директриса параболы. Парабола представляет собой множество всех точек плоскости, равноотстающих от данной точки (фокуса) и от данной прямой (директрисы). Это характеристическое свойство параболы часто принимается за определение параболы. ,
,  определяют соответственно эллипс, гиперболу и параболу, которые параллельно смещены относительно системы координат Oxy таким образом, что центр эллипса, гиперболы и вершина параболы находятся в точке
определяют соответственно эллипс, гиперболу и параболу, которые параллельно смещены относительно системы координат Oxy таким образом, что центр эллипса, гиперболы и вершина параболы находятся в точке 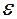 (называемая эксцентриситетом). Это свойство можно принять за определение кривых второго порядка. При этом для эллипса
(называемая эксцентриситетом). Это свойство можно принять за определение кривых второго порядка. При этом для эллипса  , для параболы
, для параболы  , для гиперболы
, для гиперболы  .
. и
и  равен 4.
равен 4. произвольная (текущая) точка искомой кривой. Запишем аналитически (в виде формулы) то свойство, которому должны удовлетворять координаты любой точки кривой. Найдем расстояние от точки
произвольная (текущая) точка искомой кривой. Запишем аналитически (в виде формулы) то свойство, которому должны удовлетворять координаты любой точки кривой. Найдем расстояние от точки  до заданных точек
до заданных точек  ;
; 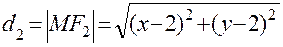 . Согласно условию задачи
. Согласно условию задачи 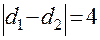 или
или .
. ;
; 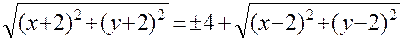 ;
;  ;
;  ;
; 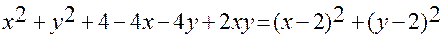 .
.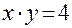 , известное из школьного курса как уравнение гиперболы, для которой оси координат являются асимптотами.
, известное из школьного курса как уравнение гиперболы, для которой оси координат являются асимптотами. и прямая
и прямая  . В декартовых координатах составить уравнение линии, каждая точка
. В декартовых координатах составить уравнение линии, каждая точка  раза ближе к точке
раза ближе к точке 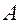 , чем к данной прямой;
, чем к данной прямой; – основание перпендикуляра, опущенного из точки
– основание перпендикуляра, опущенного из точки  . Тогда согласно условия
. Тогда согласно условия  через координаты точек это равенство запишется в виде
через координаты точек это равенство запишется в виде .
. ;
; ;
; 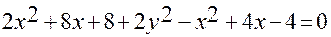 ;
;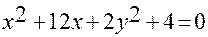 ;
; ;
; .
.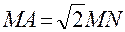 . Следовательно,
. Следовательно,  ;
; ;
; ;
; ;
; ,
, . Следовательно,
. Следовательно,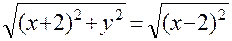 ;
; ,
, .
.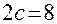 , а точка
, а точка  лежит на кривой;
лежит на кривой; ;
;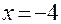 .
. . Для эллипса выполняется равенство
. Для эллипса выполняется равенство  . Точка
. Точка  .
. Эта система преобразуется к виду
Эта система преобразуется к виду 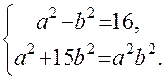
 . Исключим
. Исключим 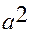 из второго уравнения:
из второго уравнения:  ,
,  ,
, 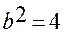 . Тогда
. Тогда  . Окончательно имеем
. Окончательно имеем  .
.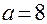 . Для гиперболы справедливо равенство
. Для гиперболы справедливо равенство  . В свою очередь
. В свою очередь  . Если учесть, что
. Если учесть, что  .
. . Искомое каноническое уравнение гиперболы имеет вид
. Искомое каноническое уравнение гиперболы имеет вид  .
. , откуда
, откуда  . Искомое каноническое уравнение параболы запишется в виде
. Искомое каноническое уравнение параболы запишется в виде  .
.