
|
|
Решение. Объём пирамиды найдем, исходя из геометрического свойствасмешанного произведения:
откуда
Элементы аналитической геометрии Аналитическая геометрия на основе метода координат изучает геометрические объекты средствами алгебры. При этом геометрическим объектам сопоставляются уравнения (системы уравнений) так, что геометрические отношения (свойства) фигур выражаются в свойствах их уравнений. Уравнение Понятие уравнения геометрического объекта дает возможность решать геометрические задачи алгебраическими методами, не прибегая к геометрическим построениям. Например, задача нахождения точек пересечения двух линий, определяемых уравнениями
Плоскость и прямая в пространстве Рассмотрим геометрические объекты, которые описываются линейными алгебраическими уравнениями. Плоскость P в декартовой прямоугольной системе координат 1) 2) вектору 3) 4) Уравнение плоскости, проходящей через три заданные точки
5) Анализируя все перечисленные уравнения плоскости, приходим к выводу: всякое уравнение первой степени Если в указанном уравнении отсутствует свободный член
ПрямаяL в пространстве может быть задана: 1) общими уравнениями как линия пересечения двух непараллельных плоскостей; 2) каноническими уравнениями
как прямая, проходящая через точку направляющему вектору 3) параметрическими уравнениями 4) уравнениями
Взаимное расположение двух плоскостей, прямой и плоскости, двух прямых в пространстве Пусть имеем две плоскости с нормальными векторами Определим угол между плоскостями и их взаимное расположение: а) Величина угла б) Плоскости P1и Р2 параллельны (перпендикулярны), если их нормальные векторы коллинеарны (ортогональны):
Расстояние d от точки
Пусть плоскость P задана уравнением Определим угол между прямой и плоскостью, и их взаимное расположение: а) Угол б) Условие параллельности прямой и плоскости:
в) Условие перпендикулярности прямой к плоскости: Пусть две прямые L1и L2 заданы уравнениями
Установим их взаимное расположение: а) Угол
б) Условие перпендикулярности двух прямых: в) Условие параллельности двух прямых:
Решение типовых задач Пример.Написать уравнение плоскости P, проходящей через точку Решение: а) Пусть б) Эту же задачу можно решить используя какое-либо уравнение плоскости. При этом решение задачи будет настолько рациональным, насколько удачно выбрано уравнение. Если его взять в виде Пример. Написать уравнение плоскости P, проходящей через две точки Решение. а)Пусть б) Решение задачи будет более простым, если воспользоваться общим уравнением плоскости
Уравнение плоскости примет вид Пример. Найти угол между плоскостью P1, проходящей через три точки Решение. Угол между плоскостями
Найдем нормальный вектор плоскости P1 через векторы
или ему коллинеарный вектор
откуда Пример. Прямая L задана общими уравнениями: Решение. Выберем одну из точек, через которую пройдет указанная прямая, заданная пересечением плоскостей. Исходная система имеет бесчисленное множество решений, одно из которых получим придавая одной из переменных конкретное значение. Пусть Решением этой системы является пара чисел В результате получим точку
Запишем канонические уравнения прямой: Обозначив равные отношения буквой t, получим параметрические уравнения прямой: Полученная ранее пропорция эквивалентна системе трех уравнений: описывающих три плоскости, проектирующие прямую на координатные плоскости Oxy, Oxz и Oyz соответственно. Чтобы найти следы прямой на координатных плоскостях, полагаем в общих уравнениях прямой последовательно системы уравнений:
Решив их, найдем следы прямой на координатных плоскостях: Замечание. Канонические уравнения прямой легко получить, записав уравнение прямой, проходящей через любые две точки, лежащие на этой прямой. Чтобы выбрать одну из них мы предположим, что решив которую, определим координаты другой точки Уравнение прямой запишем в виде
Пример. Показать, что прямые L1 : параллельны и найти расстояние Решение. Направляющим вектором прямой L2 будет вектор Ее уравнение Находим точку M1пересечения этой плоскости с прямой, заданной общими уравнениями, т.е. решим систему уравнений:
Решение ее будет тройка чисел
Прямая на плоскости Прямая на плоскости Oxy может рассматриваться как линия пересечения двух плоскостей
Эта система определяет линию (прямую) пересечения плоскости Oxy плоскостью Вектор Если заведомо известно, что прямая рассматривается на плоскости Oxy, то второе уравнение системы опускается. Тогда прямая в R2 задается одним уравнением вида Из этих рассуждений следует, что в различных по размерности пространствах одно и то же уравнение может описывать различные геометрические объекты. В рассмотренном случае линейное уравнение На основании сказанного легко получить всевозможные уравнения прямой на плоскости, исходя из аналогичных уравнений в пространстве: 1) каноническое уравнение 2) параметрические уравнения 3) уравнения прямой, проходящей через две точки, 4) уравнение прямой непараллельной оси Oy, где 5) уравнение пучка прямых, проходящих через точку
6) нормальное уравнение прямой

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
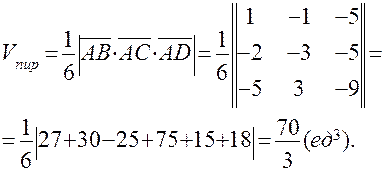
 найдем из формулы
найдем из формулы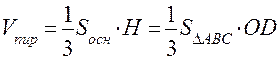 ,
,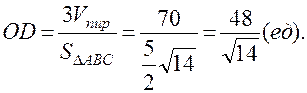
 называется уравнением поверхности (линии) в заданной системе координат, если этому уравнению удовлетворяют координаты
называется уравнением поверхности (линии) в заданной системе координат, если этому уравнению удовлетворяют координаты 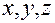 любой точки, лежащей на этой поверхности (линии), и не удовлетворяют координаты никакой другой точки, не лежащей на этой поверхности (линии).
любой точки, лежащей на этой поверхности (линии), и не удовлетворяют координаты никакой другой точки, не лежащей на этой поверхности (линии). и
и 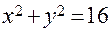 , сводится к алгебраической задаче решения системы этих уравнений.
, сводится к алгебраической задаче решения системы этих уравнений.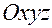 может быть задана одним из уравнений:
может быть задана одним из уравнений: – общее уравнение плоскости;
– общее уравнение плоскости;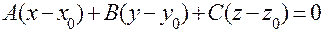 – уравнение плоскости, проходящей через точку
– уравнение плоскости, проходящей через точку 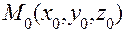 перпендикулярно нормальному
перпендикулярно нормальному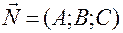 ;
; - уравнение плоскости в отрезках, где
- уравнение плоскости в отрезках, где 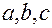 – величины направленных отрезков, отсекаемых плоскостью на координатных осях
– величины направленных отрезков, отсекаемых плоскостью на координатных осях 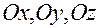 соответственно;
соответственно;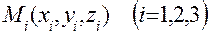 , не лежащие на одной прямой, можно записать в виде
, не лежащие на одной прямой, можно записать в виде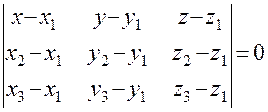 или
или  ;
;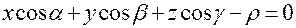 – нормальное уравнение плоскости, где
– нормальное уравнение плоскости, где 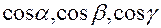 направляющие косинусы вектора
направляющие косинусы вектора 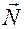 , перпендикулярного плоскости;
, перпендикулярного плоскости;  – расстояние от начала координат до плоскости.
– расстояние от начала координат до плоскости.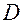 , то плоскость проходит через начало координат. Если отсутствует член с одной из координат
, то плоскость проходит через начало координат. Если отсутствует член с одной из координат 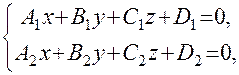
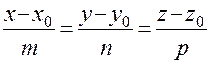 ,
,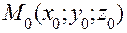 параллельно
параллельно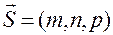 ;
;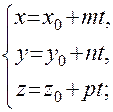
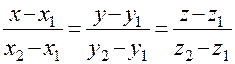 , как прямая, проходящая через две заданные точки
, как прямая, проходящая через две заданные точки  и
и  .
.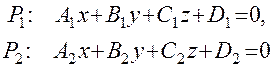
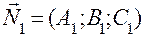 и
и 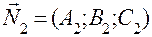 .
.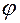 между плоскостями P1и Р2 вычисляется по формуле
между плоскостями P1и Р2 вычисляется по формуле 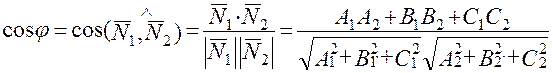 .
.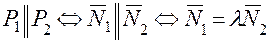 или
или  ;
;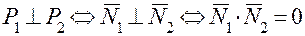 или
или 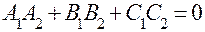 .
. .
. .
.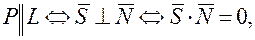 т.е.
т.е. 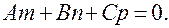

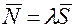 , т.е.
, т.е. 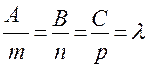 .
.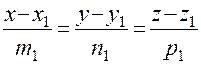 ,
,  .
.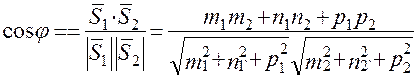 .
.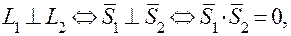 т.е.
т.е. 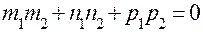 .
.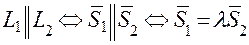 , т.е.
, т.е. 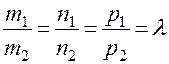 .
. перпендикулярно вектору
перпендикулярно вектору 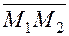 , если
, если 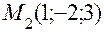 .
.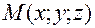 – текущая точка плоскости P. Вывести уравнение плоскости – это значит записать аналитически условие, при котором произвольная точка (текущая точка)
– текущая точка плоскости P. Вывести уравнение плоскости – это значит записать аналитически условие, при котором произвольная точка (текущая точка) 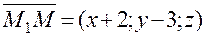 и нормального вектора плоскости
и нормального вектора плоскости 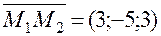 . Очевидно, что точка
. Очевидно, что точка 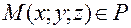 , когда указанные векторы ортогональны. Условием ортогональности этих векторов является равенство нулю их скалярного произведения, т.е.
, когда указанные векторы ортогональны. Условием ортогональности этих векторов является равенство нулю их скалярного произведения, т.е. 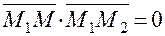 . Записав это равенство через координаты векторов, получим уравнение искомой плоскости
. Записав это равенство через координаты векторов, получим уравнение искомой плоскости 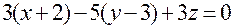 или
или 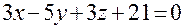 .
.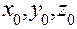 координаты точки
координаты точки 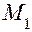 , а в качестве нормального вектора взять вектор
, а в качестве нормального вектора взять вектор 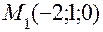 и
и 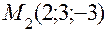 параллельно вектору
параллельно вектору 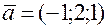 .
. и
и 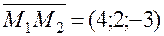 . Точка
. Точка 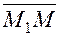 ,
, 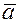 компланарны, т.е. когда
компланарны, т.е. когда 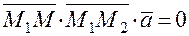 . Выразим это условие через координаты векторов:
. Выразим это условие через координаты векторов:  . Раскрыв определитель, получим уравнение плоскости вида
. Раскрыв определитель, получим уравнение плоскости вида  .
.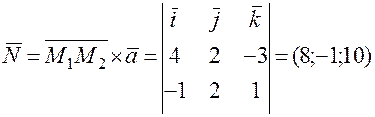 .
.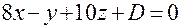 . Коэффициент D определяем из условия того, что указанная плоскость проходит через точку
. Коэффициент D определяем из условия того, что указанная плоскость проходит через точку  , откуда
, откуда 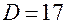 . Окончательно получим то же уравнение плоскости.
. Окончательно получим то же уравнение плоскости. ,
, 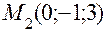 ,
, 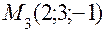 и плоскостью P2, заданной уравнением
и плоскостью P2, заданной уравнением 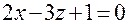 .
.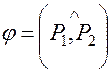 равен углу между их нормальными векторами. Поэтому
равен углу между их нормальными векторами. Поэтому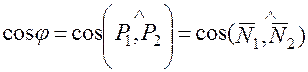 .
. ,
, 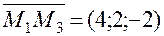 . Очевидно, в качестве этого вектора можно взять вектор
. Очевидно, в качестве этого вектора можно взять вектор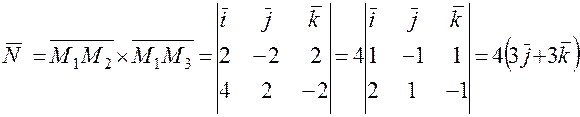
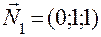 . Нормальным вектором плоскости P2 является вектор
. Нормальным вектором плоскости P2 является вектор  . Угол между плоскостями определим из равенства
. Угол между плоскостями определим из равенства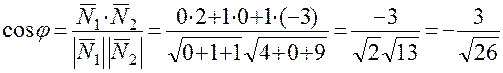 ,
,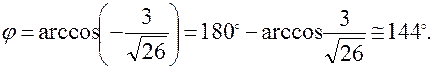
 Написать для этой прямой канонические, параметрические уравнения и уравнения в проекциях. Найти следы этой прямой на координатных плоскостях.
Написать для этой прямой канонические, параметрические уравнения и уравнения в проекциях. Найти следы этой прямой на координатных плоскостях.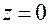 , тогда значения других неизвестных находим из системы
, тогда значения других неизвестных находим из системы 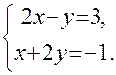
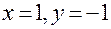 .
.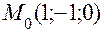 , через которую проходит искомая прямая. В качастве направляющего вектора прямой можно взять вектор
, через которую проходит искомая прямая. В качастве направляющего вектора прямой можно взять вектор  , где
, где  ,
, 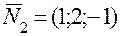 - нормальные векторы плоскостей, линией пересечения которых является прямая. Таким образом,
- нормальные векторы плоскостей, линией пересечения которых является прямая. Таким образом, .
.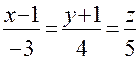 .
.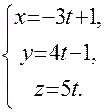
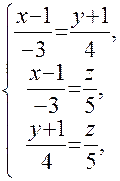 или
или 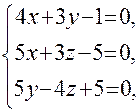
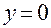 ,
, 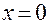 . Получим
. Получим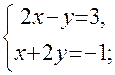
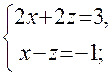
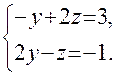
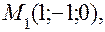
 ,
, 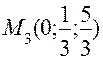 .
.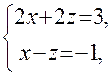
 или
или 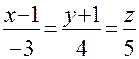 .
.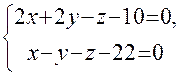 и L2:
и L2: 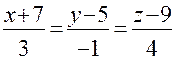
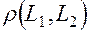 .
.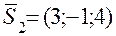 . Он ортогонален как вектору
. Он ортогонален как вектору  , так и вектору
, так и вектору 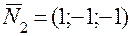 , которые являются нормальными векторами соответствующих плоскостей. Действительно, легко убедиться, что скалярные произведения
, которые являются нормальными векторами соответствующих плоскостей. Действительно, легко убедиться, что скалярные произведения  и
и 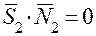 . Запишем уравнение плоскости, проходящей через точку
. Запишем уравнение плоскости, проходящей через точку 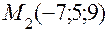 , принадлежащую прямой L2, перпендикулярно этой прямой.
, принадлежащую прямой L2, перпендикулярно этой прямой. или
или 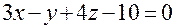 .
.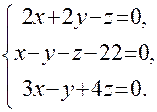
 , являющаяся координатами точки
, являющаяся координатами точки  :
:  .
. и
и 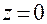 , т.е.
, т.е.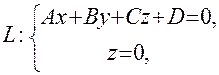 или
или 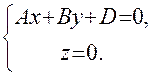
 , параллельной оси Oz.
, параллельной оси Oz.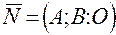 нормали плоскости
нормали плоскости  .
. , где
, где 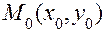 - точка, через которую проходит прямая,
- точка, через которую проходит прямая,  -ее направляющий вектор;
-ее направляющий вектор;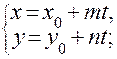
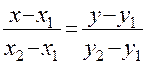 ;
;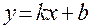 ,
, - угловой коэффициент прямой,
- угловой коэффициент прямой, 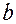 - ее начальная ордината;
- ее начальная ордината;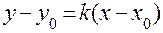 ;
;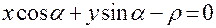 , где
, где 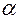 - полярный угол нормали,
- полярный угол нормали,  - расстояние прямой от начала координат.
- расстояние прямой от начала координат.