
|
|
Векторы и линейные операции над нимиВолгодонский инженерно-технический институт - филиал НИЯУ МИФИ
Методические указания К выполнению индивидуальных заданий по теме:
«Элементы векторной алгебры и аналитической геометрии» Волгодонск Элементы векторной алгебры Векторы и линейные операции над ними В геометрии вектором называют направленный отрезок Длиной (или модулем) Векторы, параллельные одной прямой, называются коллинеарными и компланарными, если они параллельны одной плоскости. Если вектор Для векторов вводятся операции сложения и вычитания. При этом заметим, что знаки «+» и «-», которые ставятся между векторами, имеют другой смысл, чем в алгебре: они обозначают не алгебраическое, а геометрическое сложение векторов по правилу треугольника или параллелограмма. Произведением вектора Сложение векторов и умножение их на число называются линейными операциями над векторами. Эти операции обладают свойствами по форме аналогичными свойствам сложения и умножения чисел. Осью называется прямая l, положительное направление которой задается единичным вектором
Проекцией (или компонентой) вектора Пусть Вектор Например, вектор Если вектор представлен как линейная комбинация некоторых векторов, то говорят, что он разложен по этим векторам. В нашем примере вектор Система n векторов Для линейной зависимости двух векторов необходима и достаточна их коллинеарность, для трех векторов – их компланарность. Если мы имеем два неколлинеарных вектора Если мы имеем три некомпланарных вектора Система n линейно независимых векторов в n -мерном пространстве называется базисом этого пространства. На плоскости два неколлинеарных вектора Базис Говорят, что в пространстве задана прямоугольная (декартовая) система координат, если в этом пространстве указан ортонормированный базис В пространственной прямоугольной системе координат вектор Если в прямоугольной системе координат точки А и В имеют координаты соответствующих координат конца В и начала А этого вектора, т.е.
а модуль его определяется как расстояние между двумя точками:
Если учесть при этом, что Пусть углы вектора Направляющие косинусы вектора Эти числа являются координатами орта Итак, задав координаты вектора, всегда можно определить его модуль и направление, т.е. сам вектор.
Линейные операции над векторами, заданными своими координатами 1) при сложении двух векторов их одноименные координаты складываются: 2) при умножении вектора Два вектора равны, если равны их соответствующие координаты, т.е. Два вектора коллинеарные, если их координаты пропорциональны. Итак, если
Умножение векторов Умножение вектора на вектор бывает двух типов: скалярное и векторное. В результате скалярного умножения двух векторов получаем число (скаляр). В результате векторного произведения двух векторов получаем вектор. Скалярным произведением Свойства скалярного произведения во многом сходны со свойствами произведения действительных чисел. Векторным произведением двух векторов 1) имеет модуль, численно равный площади параллелограмма, построенного на векторах 2) перпендикулярен к плоскости этого параллелограмма; 3) направлен в такую сторону, с которой кратчайший поворот от Отличительная особенность векторного произведения состоит в том, что для него переместительное свойство (коммутативность) не имеет места. От перестановки векторов – сомножителей векторное произведение изменяет знак на противоположный: Три вектора могут быть перемножены несколькими способами. Чаще всего рассматривают смешанное произведение двух векторов векторно и на третий скалярно.В результате получают число. Смешанное произведение трех векторов Указанные произведения векторов и их свойства достаточно просто выражаются через их прямоугольные координаты, т.е. координаты векторов в базисе Пусть заданы два вектора Скалярное произведение двух ненулевых векторов равно сумме произведений соответствующих координат этих векторов:
Угол между векторами вычисляется по формуле
или в координатной форме Проекция вектора
или в координатной форме Если учесть, что Условием перпендикулярности ненулевых векторов
Векторное произведение ненулевых векторов
Равенство нулю векторного произведения двух ненулевых векторов является условием их коллинеарности, т.е. Скаляр
Равенство нулю смешанного произведения трех ненулевых векторов является условием их компланарности:
Переход к новому базису Координаты вектора зависят от выбора базиса. Выбор базиса ничем не ограничен, и принципиальное значение имеет задача о нахождении координат вектора в одном базисе по его координатам в другом базисе. Выясним, как устанавливается связь между координатами одного и того же вектора в различных базисах. Пусть в пространстве
Матрица Обратный переход от нового базиса к старому базису осуществляется с помощью обратной матрицы Найдем зависимость между координатами некоторого вектора Подставив значения для вектора
Как нетрудно заметить, матрицей перехода от новых к старым координатам будет транспонированная матрица
Пример. В базисе Решение. Векторы
Задача сводится к решению системы:
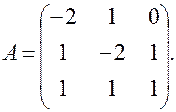
Определитель системы Связь между старым базисом Матрица перехода от старого базиса Вычисляем Находим транспонированную матрицу Координаты
Новые координаты вектора Решение типовых задач Пример. В некотором базисе Решение. Покажем, что векторы
Это же равенство удобно записать в матричной форме:
Задача сводится к решению системы: Убеждаемся в том, что определитель системы не равен нулю. Поэтому однородная система имеет только нулевое решение. Следовательно,
Запишем это равенство в координатной форме:
От этого равенства переходим к решению системы уравнений:
Решением этой системы является тройка чисел
Пример: Даны четыре точки
1) Вычислить значение выражения Решение. Находим координаты векторов Найдем их линейную комбинацию:
Вычислим модуль полученного вектора:
2) Найти Решение. Найдем координаты векторов
Найдем модули полученных векторов и их скалярное произведение:
Определяем косинус угла между векторами:
Найдем проекцию вектора
2) Определить длину медианы Решение. Определим координаты точки Вычислим длину медианы
3) Вычислить площадь Решение. Площадь треугольника найдем, исходя из геометрического свойства векторного произведения: Найдем векторное произведение:
= Тогда
Определим высоту 4) Найти объём пирамиды 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 с начальной А и конечной В точками, который можно перемещать параллельно самому себе. Таким образом, считается, что два направленных отрезка
с начальной А и конечной В точками, который можно перемещать параллельно самому себе. Таким образом, считается, что два направленных отрезка  , имеющие равные длины и одно и то же направление, определяют (изображают) один и тот же вектор
, имеющие равные длины и одно и то же направление, определяют (изображают) один и тот же вектор 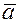 , и пишут
, и пишут  .
. вектора
вектора  , называется вектором, противоположным вектору
, называется вектором, противоположным вектору  называется вектор
называется вектор  , имеющий длину
, имеющий длину 
 , направление которого совпадает с направлением вектора
, направление которого совпадает с направлением вектора  , если
, если  , и противоположно ему, если
, и противоположно ему, если  .
. . Пусть
. Пусть  - произвольный вектор, а А1, В1 ортогональные проекции точек А и В на ось l.
- произвольный вектор, а А1, В1 ортогональные проекции точек А и В на ось l.
 ), такое, что
), такое, что  . Число
. Число  на ось l и обозначается
на ось l и обозначается  . Координата
. Координата  и со знаком «-», если
и со знаком «-», если  . Справедливо равенство
. Справедливо равенство  . Часто именно это число называют проекцией вектора
. Часто именно это число называют проекцией вектора  - векторы, а
- векторы, а  - действительные числа.
- действительные числа. называется линейной комбинацией векторов
называется линейной комбинацией векторов  .
. является линейной комбинацией векторов
является линейной комбинацией векторов  .
. разложен по векторам
разложен по векторам  называется линейно независимой, если из этих векторов невозможно составить нулевую линейную комбинацию, в которой хотя бы один из коэффициентов
называется линейно независимой, если из этих векторов невозможно составить нулевую линейную комбинацию, в которой хотя бы один из коэффициентов  был бы отличен от нуля. Иными словами, векторы
был бы отличен от нуля. Иными словами, векторы  возможно лишь тогда, когда все
возможно лишь тогда, когда все  . В противном случае система векторов линейно зависимая.
. В противном случае система векторов линейно зависимая. может быть единственным способом разложен по векторам
может быть единственным способом разложен по векторам  .
. может быть однозначно разложен по векторам
может быть однозначно разложен по векторам  .
. , где
, где  не равны нулю одновременно.
не равны нулю одновременно. , а в пространстве тройка некомпланарных векторов
, а в пространстве тройка некомпланарных векторов  , взятых в определенном порядке, образуют базис.
, взятых в определенном порядке, образуют базис. называется ортонормированным, если векторы
называется ортонормированным, если векторы  .
. определяют положительное направление трех координатных осей: Оx (оси абсцисс), Oy (оси ординат) и Oz (оси аппликат), соответственно.
определяют положительное направление трех координатных осей: Оx (оси абсцисс), Oy (оси ординат) и Oz (оси аппликат), соответственно. , где
, где  - координаты вектора
- координаты вектора  .
. и
и  , то координаты вектора
, то координаты вектора  ,
,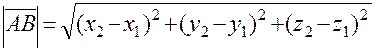 .
. , то выражение для модуля вектора можно записать так:
, то выражение для модуля вектора можно записать так:  .
. .
. ;
;  ;
;  .
. , т.е.
, т.е.  , и связаны равенством
, и связаны равенством  .
. и
и  , выполняются по следующим правилам:
, выполняются по следующим правилам: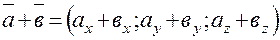 ;
; на число
на число  .
. .
. , то
, то  или
или 
 .
. двух ненулевых векторов
двух ненулевых векторов  , где
, где 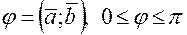 .
. , который:
, который: ;
; называется правой тройкой векторов).
называется правой тройкой векторов). .
. ,
,  или
или  , есть скаляр, абсолютная величина которого равна обьему параллелепипеда, построенного на векторах
, есть скаляр, абсолютная величина которого равна обьему параллелепипеда, построенного на векторах  , которых мы не приводим.
, которых мы не приводим. и
и  .
. .
. ,
, .
. ,
, .
. - орт вектора, то
- орт вектора, то  .
. .
. выражается через координаты данных векторов
выражается через координаты данных векторов  .
.

 , представляющий смешанное произведение трех векторов, равняется определителю третьего порядка, составленному из координат этих трех векторов:
, представляющий смешанное произведение трех векторов, равняется определителю третьего порядка, составленному из координат этих трех векторов: .
. .
. имеются два базиса: старый
имеются два базиса: старый  . Каждый из векторов
. Каждый из векторов  (i =1,2,3) нового базиса можно выразить в виде линейной комбинации векторов старого базиса:
(i =1,2,3) нового базиса можно выразить в виде линейной комбинации векторов старого базиса: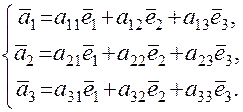 .
. (i,k=1,2,3) называется матрицей перехода от старого базиса к новому. Базисные векторы
(i,k=1,2,3) называется матрицей перехода от старого базиса к новому. Базисные векторы  (i =1,2,3) линейно независимы, поэтому матрица
(i =1,2,3) линейно независимы, поэтому матрица 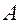 неособенная.
неособенная. .
. в разных базисах. Пусть этот вектор имеет координаты
в разных базисах. Пусть этот вектор имеет координаты  относительно старого базиса и координаты
относительно старого базиса и координаты  относительно нового базиса, т.е.
относительно нового базиса, т.е.  и
и 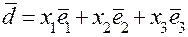
 из предыдущей системы в первое равенство
из предыдущей системы в первое равенство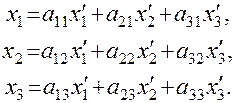
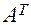 . В матричном виде взаимосвязь между старыми координатами и новыми выражается следующими равенствами:
. В матричном виде взаимосвязь между старыми координатами и новыми выражается следующими равенствами: и
и  .
. и вектор
и вектор  . Показать, что векторы
. Показать, что векторы  образуют базис, если они линейно независимы. Составим векторное равенство
образуют базис, если они линейно независимы. Составим векторное равенство 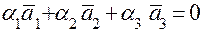 или
или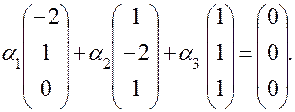
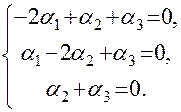
 не равен нулю. Следовательно, однородная система имеет только нулевое решение
не равен нулю. Следовательно, однородная система имеет только нулевое решение  , значит векторы
, значит векторы  выражается системой уравнений:
выражается системой уравнений: 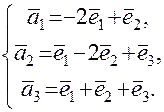


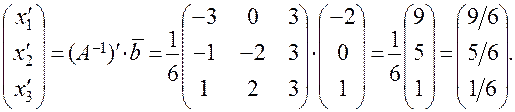

 , а также вектор
, а также вектор  . Показать, что векторы
. Показать, что векторы 
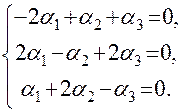
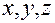 – координаты вектора
– координаты вектора  .
.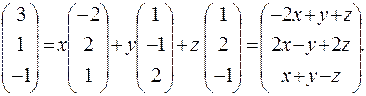
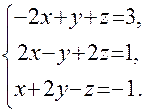
 . Они также являются координатами вектора
. Они также являются координатами вектора  или
или  .
.
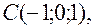
 .
. , где
, где 

 ,
,  .
. .
. .
. .
. и
и  , где
, где  ,
,  .
. ,
,  .
. ,
,  ,
, .
.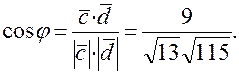
 .
. и стороны
и стороны  в треугольнике
в треугольнике  .
. как средней точки между
как средней точки между  и
и  :
:  ;
;  ;
;  ;
;  .
. и стороны
и стороны  :
: ;
; .
. и его высоту
и его высоту  .
. .
.
 .
.
 .
. , исходя из формулы
, исходя из формулы 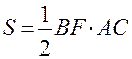 , откуда
, откуда  .
. .
.