
|
|
Базис - максимальная упорядоченнаясистема линейно независимых векторов. Если векторы
На плоскости 2 любых неколлинеарных вектора образуют базис. ДПБ-базис, состоящий из ортогональных еденичных векторов.
Операции над векторами в координатной форме.
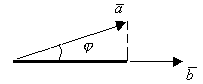
направляющие косинусы
__________________________________________________________________
Скалярное произведение векторов, его свойства, вычисление. Скалярное произведение векторов Опр. Скалярным произведением векторов наз-ся скалярное произведение длин этих векторов на косинус угла между ними. Если вектор нулевой, то все произведения-ноль Св-ва скалярного произведения. 1. Если 2. 3. 4. 5. 6. ( скалярное произведение в координатах) Условие ортоганальности векторов Условие коллинеарности векторов Скалярный квадрат
__________________________________________________________________ Векторное произведение, его свойства, вычисление. Свойства векторного произведения. 1. Если 2 вектора коллиниарны , их произведение = 0
2. Если поменять местами сомножители, меняется знак
3. 4. 5.
Пример.
__________________________________________________________________ Смешанное произведение трех векторов, его свойства, геометрический смысл, вычисление. Смешанное произведение векторов.
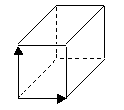
Свойства смешанного произведения. 1. 2. 3. Геометрический смысл смешанного произведения векторов: 1) Абсолютная величина смешанного произведения векторов
__________________________________________________________________ АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ Прямая линия на плоскости. Различные уравнения прямой. Угол между прямыми, условия параллельности и перпендикулярности прямых на плоскости.
Теорема: Всякое линейное ур-ние вида Векторное ур-е прямой.
Параметрическое уравнение прямой.
Условие параллельности двух прямых.
Условие перпендикулярности двух прямых.
Угол между двумя прямыми
__________________________________________________________________
Плоскость в пространстве. Угол между плоскостями, условия параллельности и перпендикулярности плоскостей. Плоскость в пространстве.
Опр: Любое линейное уравнение от 3-х переменных определяет пл-ть в пространстве и обратно.
ур-е пл-ти, проходящей через данную точку и данный нормальный вектор
Пусть
Нормальное уравнение плоскости.
p - расстояние от начала координат до плоскости. Условие параллельности двух плоскостей.
Условие перпендикулярности двух плоскостей.
Угол между плоскостями.
__________________________________________________________________ Прямая линия в пространстве. Общие и канонические уравнения прямой в пространстве. Прямая в пространстве.
t=
Пример.
Условие параллельности 2-х прямых
Если __________________________________________________________________ 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 ,
, 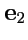 ,
,  взаимно ортогональны и по модулю равны единице, то они называются ортами прямоугольной декартовой системы координат, а сам базис ортонормированным декартовым базисом. Орты декартовой системы координат обычно обозначают как
взаимно ортогональны и по модулю равны единице, то они называются ортами прямоугольной декартовой системы координат, а сам базис ортонормированным декартовым базисом. Орты декартовой системы координат обычно обозначают как  ,
,  ,
,  .
.
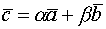
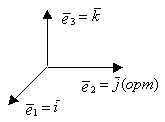
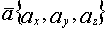
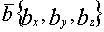
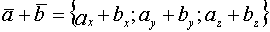
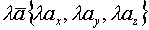

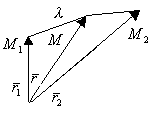
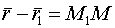
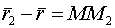
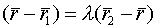
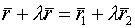
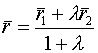


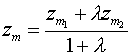
 -нач.точка
-нач.точка  -кон.точка
-кон.точка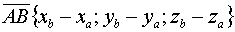
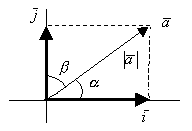

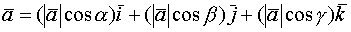
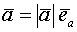
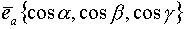

 и
и 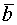 ортоганальны
ортоганальны 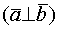 , то
, то 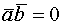
 если
если  ;
;  если
если 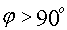
 (коммутативность)
(коммутативность) (дистрибутивность)
(дистрибутивность)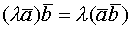
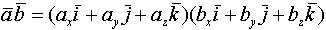 =
=  =
= 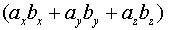
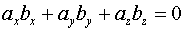
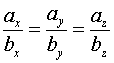
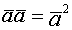

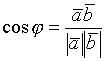
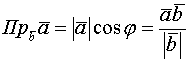
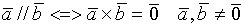
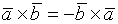 (антикоммутативность)
(антикоммутативность)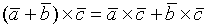
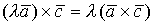
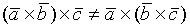
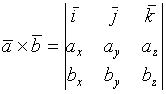

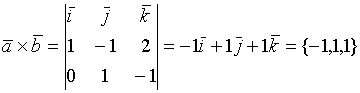
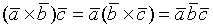
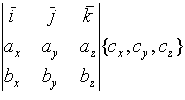 =
= 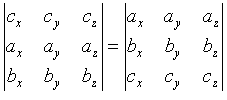 =
=  =
= 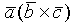
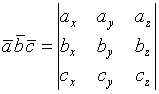
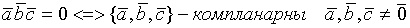

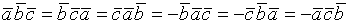
 ,
,  ,
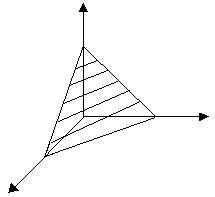
, 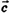 численно равна объему V1 параллелепипеда, построенного на этих векторах, т. е. V1 = |
численно равна объему V1 параллелепипеда, построенного на этих векторах, т. е. V1 = |  , V2 - объем треугольной пирамиды, построенной на векторах
, V2 - объем треугольной пирамиды, построенной на векторах 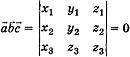
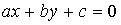 (oбщее ур-е прямой) определяет прямую на плоскости.
(oбщее ур-е прямой) определяет прямую на плоскости.
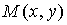 ;
; 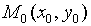 ;
;  ;
; 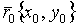
 ;
;  -векторное ур-е прямой
-векторное ур-е прямой -ур-е прямой проходящей через данную точку с данным нормальным вектором
-ур-е прямой проходящей через данную точку с данным нормальным вектором 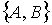

 -ур-е прямой проходящей через данную точку с заданным вектором(каноническое ур-е)
-ур-е прямой проходящей через данную точку с заданным вектором(каноническое ур-е)
 ;
;  , т.к.
, т.к.  или
или 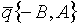
 ,где
,где  - ур-ние прямой проходящей через заданную точку с данным угловым коэффициентом.
- ур-ние прямой проходящей через заданную точку с данным угловым коэффициентом. -ур-ние прямой с данным угловым коэффициентом.
-ур-ние прямой с данным угловым коэффициентом. -ур-ние прямой проходящей через 2 заданные точки.
-ур-ние прямой проходящей через 2 заданные точки.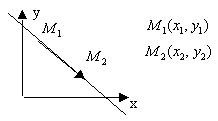
 - ур-ние прямой в отрезках
- ур-ние прямой в отрезках
 - нормальное ур-е прямой
- нормальное ур-е прямой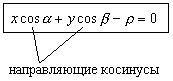
 -расстояние от начала координат до прямой
-расстояние от начала координат до прямой 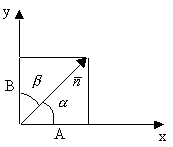
 ;
; 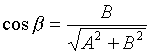
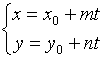

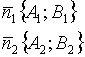
 ;
; 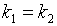
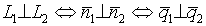

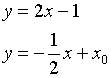
 .
. =
= 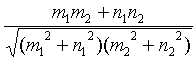
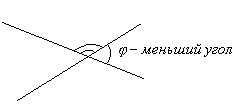


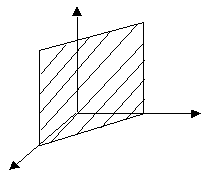
 - общее ур-е пл-ти в пространстве
- общее ур-е пл-ти в пространстве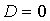 -пл-ть проходит через начало координат
-пл-ть проходит через начало координат 
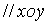

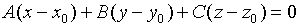
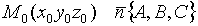

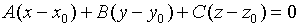


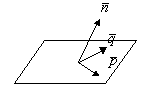
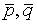 -направляющие вектора пл-ти
-направляющие вектора пл-ти
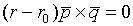
 -смешанное произведение 3-х векторов
-смешанное произведение 3-х векторов - ур-е пл-ти проходящей через данную точку с данными направляющими векторами.
- ур-е пл-ти проходящей через данную точку с данными направляющими векторами.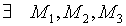
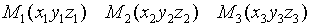
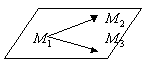
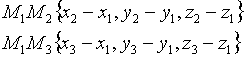
 x,y,z -текущие координаты
x,y,z -текущие координаты
 - ур-е пл-ти в отрезках.
- ур-е пл-ти в отрезках.
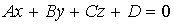
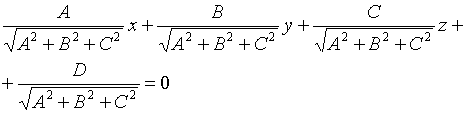
 -нормальное ур-е пл-ти
-нормальное ур-е пл-ти ;
; 


 ;
;  ;
; 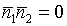
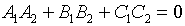

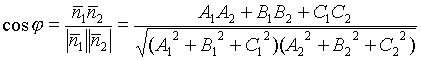


 - векторное ур-е прямой в пространстве
- векторное ур-е прямой в пространстве каноническое ур-е прямой
каноническое ур-е прямой - параметрическое ур-е прямой в пространстве
- параметрическое ур-е прямой в пространстве
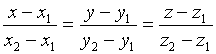 - ур-е прямой прох. через 2 данные точки
- ур-е прямой прох. через 2 данные точки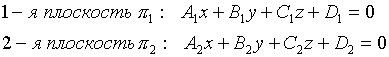
 - общее ур-е прямой в пространстве
- общее ур-е прямой в пространстве
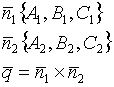
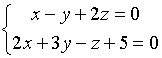

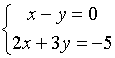

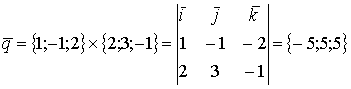

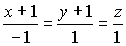
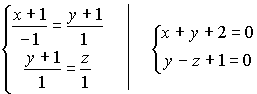


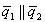 ;
;  ;
; 
 , то прямые перпендикулярны ортогонально.
, то прямые перпендикулярны ортогонально.