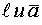|
|
Исследование систем линейных алгебраических уравнений. Теорема Кронекера-Капелли. Однородные системы линейных алгебраических уравнений.Исследование систем линейных уравнений. Теорема Кронекера-Капелли. Рассмотрим систему линейных уравнений (*) А=( Т. Кронекера-Капелли. Система уравнений (*) совместна тогда и только тогда, когда ранг матрицы системы А равен рангу расширенной матрицы r(A)=r(H) Если система совместна, то она имеет единственное решение, если r(A)=r(H)=n и его можно найти методами Крамера или Гаусса. Если r(A)=r(H)=k<n, то система имеет бесконечно много решений. В этом случае n-k неизвестных обьявляются свободными неизвестными (принимают любые значения), оставшиеся kнеизвестных выражаются через эти свободные неизвестные.
Однородные системы линейных уравнений Если в системе (*) все свободные члены Однородные системы всегда совместны т.к. 1) 2) Если ранг матрицы А меньше числа неизвестных,то система имеет бесконечно много решений Свойства решений линейной однородной системы уравнений. 1) Если Доказательство.
2) Если
Доказательство.
+
откуда получим 3) Если также является решением системы. Доказательство.
+
откуда получим Каждое из решений системы можно записать в виде строки матрицы Пример.
{
__________________________________________________________________ ВЕКТОРНАЯ АЛГЕБРА. 1) Геометрический вектор. Равенство векторов, коллинеарность, компланарность. Линейные операции над векторами.
Геометрический вектор Понятие вектора Вектор: отрезок с началом в точке А и концом в точке В.
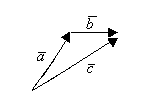
Два вектора Два вектора называются коллинеарными, если они параллельны. Три вектора называются компланарными, если они лежат в одной плоскости. Линейные операции над векторами. А) Умножение вектора на число. Б) Сложение векторов 1) 2) 3) Таким образом операции обладают св-ми. 1) 2) Вектор у которого начало и конец совпадают есть нулевой вектор 3) 4) 5) 6) 7) 8) Вычитание- обратное сложению. __________________________________________________________________
Линейная зависимость векторов. Базис. Декартов базис. Линейная зависимость векторов, теоремы о линейной зависимости. Опр 1. Система векторов Система векторов Выражение стоящее в левой части рав-ва (1) наз-ют линейной комбинацией векторов Опр 2. Система векторов является линейно зависимой, если существует линейная комбинация этих векторов с неравными 0 числами, которая тождественно равна. Теор 1. Если система векторов Док-во. Пусть
Теор 2. Если к системе линейно зависимых векторов Док-во. Т.К. система векторов
Есть
Следовательно система линейно зависима. Следствие. Если к линейно зависимой системе добавить любое кол-во векторов, то полученная система будет линейно зависима. Теор. (О линейной зависимости двух векторов.) Два вектора линейно зависимы тогда и только тогда, когда они коллинеарны. Док-во.
Теор. Три вектора линейно зависимы тогда и только тогда, когда они компланарны Док-во.
Для Теор. В трехмерном пространстве любые 4 вектора линейно зависимы. Док-во.
Вектор в системе координат 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
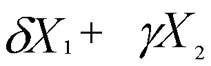
 ) H=
) H= 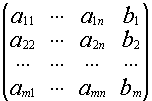
 равны нулю, то такая система является однородной.
равны нулю, то такая система является однородной. =
= 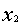 =
=  =
=  =0 всегда является решением. Такое решение называется тривиальным.
=0 всегда является решением. Такое решение называется тривиальным.
 то
то 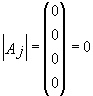
 является решением системы, то
является решением системы, то 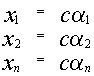 также является решением.
также является решением.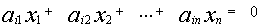
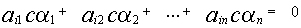
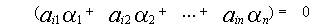
 также является решением той же самой системы, то и
также является решением той же самой системы, то и также является решением системы
также является решением системы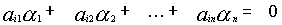
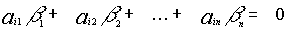
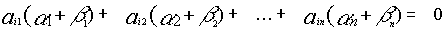

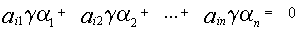
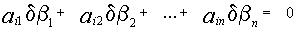
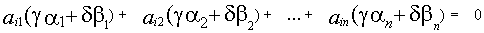
 , тогда на основании свойств можно утверждать, что матрицы
, тогда на основании свойств можно утверждать, что матрицы  есть решения, то
есть решения, то 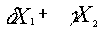 также являются решением. Минимальная возможная система решений через которую выражаются все остальные решения называется фундаментальной системой решений.
также являются решением. Минимальная возможная система решений через которую выражаются все остальные решения называется фундаментальной системой решений.
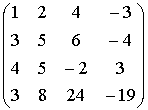 ~
~ 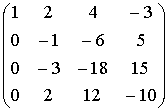 ~
~ 
 {
{ 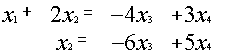
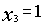
 {
{  {
{ 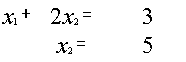

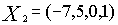
 Обозначается:
Обозначается: 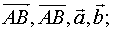
 равны, если они совпадают при параллельном переносе.
равны, если они совпадают при параллельном переносе.
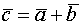


 -длину вектора умножить на
-длину вектора умножить на 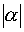 и оставить направление вектора если
и оставить направление вектора если 
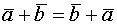
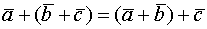
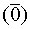
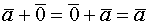

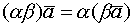
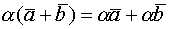
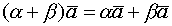
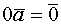
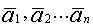 называется линейно зависимой, если сущ. числа
называется линейно зависимой, если сущ. числа  не все равные 0, такие что
не все равные 0, такие что  (1)
(1) , тогда
, тогда 
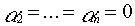
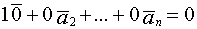
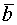 , то вновь полученная система будет линейно зависима.
, то вновь полученная система будет линейно зависима. (3)
(3) (4)
(4) ,
,  0 -не все равны нулю
0 -не все равны нулю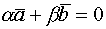
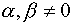
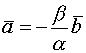
 -коллинеарны
-коллинеарны
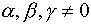
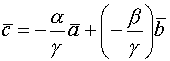

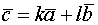
 и
и  пл-ть
пл-ть  , что
, что 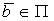 (или //) и
(или //) и 

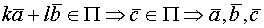 либо
либо  , либо // ей
, либо // ей 
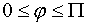

 -угол между
-угол между