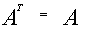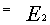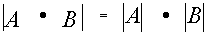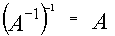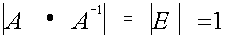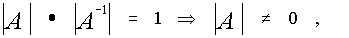|
|
Понятие обратной матрицы.ОПРЕДЕЛИТЕЛИ. МАТРИЦЫ. Определители второго и третьего порядка. Свойства определителей. Определители второго порядка. Пусть дана матрица второго порядка A= Определителем второго порядка называется число, вычисляемое по правилу:
Определитель второго порядка равен произведению элементов Главной диогонали минус произведение элементов Побочной дио- гонали.
ОПРЕДЕЛИТЕЛИ ТРЕТЬЕГО ПОРЯДКА. Определителем третьего порядка называется число, вычисляемое по правилу:
Определитель третьего порядка равен сумме произведений элементов первой строки на их алгебраические дополнения. Заменим алгебраические дополнения на миноры:
Вычисляя миноры, получим:
СВОЙСТВА ОПРЕДЕЛИТЕЛЕЙ. Свойство 1. При замене строк на столбцы определитель не меняется.
(такая операция называется транспонированием). Следствие: строки и столбцы равноправны ,т.е любые свойства или утверждения относительно строк справедливы и для столбцов и наоборот. Свойство 2. При перестановке двух строк определитель меняет знак на противоположный.
Следствие: любую строку (столбец ) можно поставить первой (первым) Свойство 3. Определитель с двумя равными строками равен нулю.
Свойство 4. Общий множитель элементов строки можно выносить за знак определителя.
Следствие : Постоянный множитель можно внести в какую-нибудь строку
Свойство 5. Если элементы какой –либо строки состоят из двух слагаемых, то определитель можно представить в виде суммы двух определите- лей.
Свойство 6. Определитель не меняется ,если любую строку умножить на любое число и прибавить к любой другой строке.
Случаи ,когда определитель равен нулю:
______________________________________________________________________ Свойства определителей. Определители 2-го порядка. Формулы Крамера. Формулы Крамера Расмотрим систему уравнений (*). И пусть А- матрица системы
Если i –столбец заменим свободными членами , то соответствующую матрицу обозначим
Если система линейных уравнений (*) такова, что определитель системы отличен от нуля ,то система линейных уравнений имеет единственное решение , которое находится по формуле:
______________________________________________________________________
Матрицы. Виды матриц. Линейные операции над матрицами. Произведение матриц. Две матрицы A и B называются равными ,если они имеют один и тот же порядок и если элементы стоящие на соответствующих местах равны.
К линейным операциям относятся : Умножение матрицы на число Для того чтобы умножить матрицу на число нужно каждый элемент матрицы умножить на это число:
Сложение матриц. Складывать можно только матрицы одинаковых размеров:
Свойства линейных операций
Если матрица в качестве элементов имеет нули , то такая матрица называется нулевой. Произведение матриц .
Пример:
Если для матриц А и В выполняется равенство А* В=В*А ,то матрицы называются перестановочными. Если для матриц А , В , С имеет смысл операция произведения, то выполняются равенства A(B*C)=(A*B)*C A(B+C)=AB+AC (B+C)A=BA+CA Транспонирование матриц Рассмотрим матрицы
AT называется транспонированной по отношению к A Если AT получена из матрицы А заменой строк на столбцы то
Очевидно: Если А является квадратной матрицей(n*n), то элементы матрицы Если для квадратной матрицы выполняется условие
то матрица А называется симметричной и в этом случае достаточно указать элементы, стоящие на главной диагонали и элементы, стоящие над главной диагональю. __________________________________________________________________ Обратная матрица и ее вычисление методом Крамера (методом присоединенной матрицы). Метод элементарных преобразований вычисления обратной матрицы. Понятие обратной матрицы. Обратные матрицы существуют только для квадратных матриц. Квадратная матрица ,у которой на главной диагонали стоят единицы, а вне главной диагонали - нули, называется единичной матрицей. Например, единичная матрица второго порядка:
Теорема. Если А и В – квадратные матрицы одного и того же порядка n, то определитель их произведения равен произведению определителей матриц-сомножителей:
Определение обратной матрицы: Матрица В называется обратной для матрицы А , если А и В перестановочны и А*В=В*А=Е Обозначение обратной матрицы:
Теорема. Если матрица А имеет обратную ,то ее определитель отличен от нуля. Доказательство. Так как А имеет обратную матрицу, то
Воспользуемся теоремой о том ,что определитель произведения равен произведению определителей.
что и требовалось доказать. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 .
.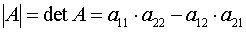
 = 1*(-4)-6 = -10
= 1*(-4)-6 = -10 =
=  =
= 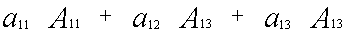
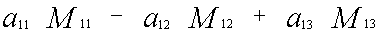

 -
- 
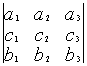 +
+ 
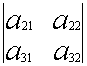
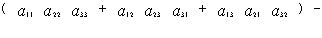
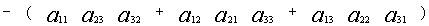
 =
= 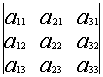
 = -
= - 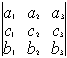
 = 0
= 0
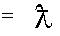
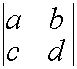



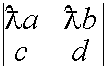


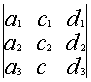


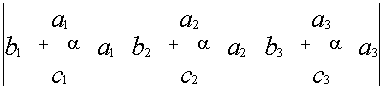
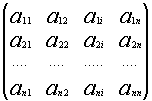

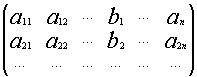
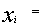

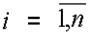

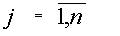
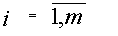
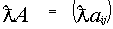
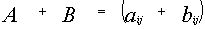
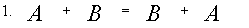
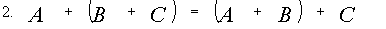
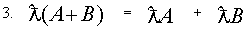
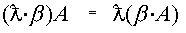
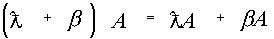



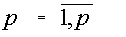
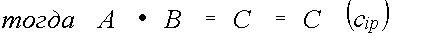
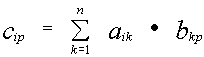


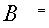
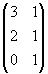

 =
= 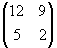

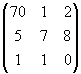
 .
.


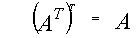
 назавают главной диагональю
назавают главной диагональю