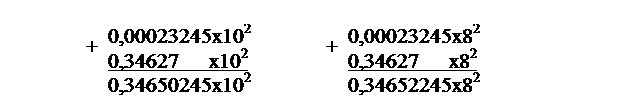|
|
Компьютерное представление вещественных чиселСуществуют два основных типа представления чисел в компьютере, называемые представлениями с фиксированной и с плавающей запятой. При представлении чисел с фиксированной запятой все разряды ячейки, кроме знакового разряда, если он есть, служат для изображения разряда числа. Место запятой фиксируется перед определенным разрядом (для целых чисел запятая находится после младшего разряда, т.е. вне разрядной сетки). Именно поэтому такое представление получило название с фиксированной запятой. Для представления вещественных чисел в современных компьютерах принят способ представления с плавающей запятой. Этот способ представления опирается на нормализованную (экспоненциальную) запись вещественных чисел. Нормализованная запись числа Нормализованная запись отличного от нуля вещественного числа – это запись вида Примеры нормализации чисел 1) 3,1415926=0,31415926 х 101; 2) 1000=0,1 х 104; 3) 0,123456789=0,123456789 х 100; 4) 0,00001078=0,1078 х 8-4; 5) 1000,00012=0,100000012 х 24. Представление чисел с плавающей запятой При представлении числа с плавающей запятой часть разрядов ячейки отводится для записи порядка числа, остальные разряды – для записи мантиссы. По одному разряду в каждой группе отводится для записи знака порядка и знака мантиссы. Например, можно представить такое распределение разрядов ячейки памяти:
Первые два разряда служат для изображения знаков порядка и мантиссы соответственно: 0 – если знак «плюс», 1 – знак «минус». Следующие k разрядов используются для изображения абсолютной величины порядка числа, остальные n разрядов используются для изображения абсолютной величины мантиссы. На точность вычислений оказывает влияние длина мантиссы, а количество разрядов, отводимых под порядок, влияет на допустимый диапазон представляемых чисел. Очевидно, чем большая точность нам требуется, тем более «длинную» ячейку придется использовать. Арифметические операции над числами Арифметические операции над числами, представленными в позиционной СС, выполняются одинаково, независимо от того, в какой позиционной СС представлены числа. Из курса школы должны быть известны некоторые простые приемы оперирования над числами, например, простые арифметические операции, так как сложение, вычитание, умножение, деление можно удобно выполнять с помощью записи в виде так называемого «столбика». Система счисления, в которой мы привыкли работать, называется десятичной, в данной системе каждый разряд кратен десяти, т.е. число Сложение и вычитание Как излагалось ранее, сложение и вычитание чисел можно удобно выполнять «столбиком», учитывая основу СС и правила арифметики для данной СС. Разберем пример сложения двух чисел данных в десятичной и восьмеричной СС:
Из примеров видно, что сложение в восьмеричной СС делается так же, как и для десятичной СС, только необходимо пользоваться правилами арифметики соответствующей СС. Для выполнения арифметических операций над вещественными числами необходимо провести подготовительное действие, называемое выравниванием порядков. Порядок меньшего по модулю числа при этом становится равным порядку большего. Для этого мантисса числа с меньшим порядком сдвигается в ячейке вправо на количество разрядов, равное разности порядков данных чисел. Таким образом, одинаковые разряды чисел оказываются расположенными в одних и тех же разрядах. После описанного преобразования сложение и вычитание мантисс чисел выполняется так же, как и над числами с фиксированной запятой. Пример. Необходимо сложить числа Перед сложением необходимо провести выравнивание порядков чисел:
Вычитание чисел делается аналогичным способом, приведенным для операции сложения. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
 , где q – целое число (положительное, отрицательное или ноль), а m – правильная P-ичная дробь, у которой первая цифра после запятой не равна нулю, т.е.
, где q – целое число (положительное, отрицательное или ноль), а m – правильная P-ичная дробь, у которой первая цифра после запятой не равна нулю, т.е.  . При этом m называется мантиссой числа, q – порядком числа.
. При этом m называется мантиссой числа, q – порядком числа.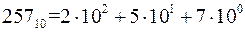 для восьмеричной СС число 257 можно представить следующим образом:
для восьмеричной СС число 257 можно представить следующим образом:  . Аналогично можно показать представление числа в любой другой позиционной СС.
. Аналогично можно показать представление числа в любой другой позиционной СС.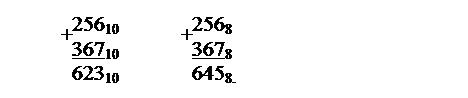
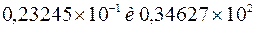 , представленные в десятичной системе счисления, и числа
, представленные в десятичной системе счисления, и числа  , представленные в восьмеричной СС.
, представленные в восьмеричной СС.