
|
|
Позиционные системы счисленияАлгоритмические языки и программирование
Позиционная Система счисления
Методические указания к выполнению лабораторной работы №1 для студентов очной формы обучения специальности 230201 – "Информационные системы и технологии"
Брянск 2007 УДК 004.43
Алгоритмические языки и программирование. Позиционная система счисления: методические указания к выполнению лабораторной работы №1 для студентов очной формы обучения специальности 230201 – "Информационные системы и технологии". – Брянск: БГТУ, 2007. - 12 с.
Разработали: Ю.А. Леонов, асс. С.М. Рощин, к.т.н.
Научный редактор Ю.М. Казаков Редактор издательства Л.И. Афонина Компьютерный набор Ю.А. Леонов Рекомендовано кафедрой «Компьютерные технологии и системы» БГТУ (протокол № от )
Темплан 2007г., п. 460
Издательство брянского государственного технического университета, 241035, Брянск, бульвар 50-летия Октября, 7, БГТУ. 58-82-49 Лаборатория оперативной полиграфии БГТУ, ул. Харьковская, 9 ЦЕЛЬ РАБОТЫ Целью работы является ознакомление с видами систем счисления (СС) и приобретение практических навыков перевода из одной СС в другую, а также овладение элементарными арифметическими операциями над числами. Продолжительность работы – 2ч. Теоретическая часть Совокупность приемов наименования и обозначение чисел называется системой счисления. В качестве условных знаков для записи чисел используются цифры.Система счисления, в которой значение каждой цифры в произвольном месте последовательности цифр, обозначающей запись числа, не изменяется, называется непозиционной. Система счисления, в которой значение каждой цифры зависит от места в последовательности цифр в записи числа, называется позиционной. Позиционные системы счисления Общепринятой в современном мире является десятичная позиционная система счисления (СС), которая из Индии через арабские страны пришла в Европу. Основой данной системы является число десять. Основой СС называется число, означающее, во сколько раз единица следующего разряда больше, чем единица предыдущего. Общеупотребительной формой записи числа является сокращенная форма записи разложения по степеням основы СС, например, для десятичной СС число 130678 будет выглядеть следующим образом:
Здесь 10 служит основой СС, а показатель степени - это вес разряда цифры (нумерация ведется справа налево, начиная от нуля). Арифметические операции в этой системе выполняют по правилам, предложенным еще в средневековье. Проблема выбора СС для представления чисел в памяти компьютера имеет большое практическое значение. В случае ее выбора обычно учитываются такие требования, как надежность представления чисел при использовании физических элементов, экономичность (использование таких СС, в которых количество элементов для представления чисел из некоторого диапазона было бы минимальным). Для представления целых чисел от 0 до 99 в десятичной системе достаточно двух разрядов, то есть двух элементов. Поскольку каждый элемент может находиться в десяти состояниях, то общее количество состояний – 102, в двоичной системе исчисления: 9910=11000112, необходимое количество состояний - 27 (индекс внизу числа - основа системы исчисления). Из приведенного примера видно, что для представления одного и того же числа в десятичной СС требуется меньше разрядов, чем в двоичной СС.
Более распространенной для представления чисел в памяти компьютера является двоичная СС. Для изображения чисел в этой системе необходимо две цифры: 0 и 1, то есть достаточно двух стойких состояний физических элементов. Эта система близка к оптимальной по экономичности, и кроме того, таблицы сложения и умножения в этой системе элементарные (табл.1).
Поскольку 23=8, а 24=16, то каждых три двоичных разряда числа образовывают один восьмеричный, а каждых четыре двоичных разряда - один шестнадцатеричный. Поэтому для сокращения записи адресов и содержимого оперативной памяти компьютера используют шестнадцатеричную и восьмеричную СС. В табл.2 приведены первые 16 натуральных чисел, записанных в десятичной, двоичной, восьмеричной и шестнадцатеричной СС. Для отладки программ и в других ситуациях в программировании актуальной является проблема перевода чисел из одной позиционной системы исчисления в другую. Если основа «новой» СС равняется некоторой степени «старой» СС, то алгоритм перевода очень простой: нужно сгруппировать справа налево разряды в количестве, равном показателю степени, и заменить эту группу разрядов соответствующим символом новой СС. Этим алгоритмом удобно пользоваться при переводе числа из двоичной СС в восьмеричную или шестнадцатеричную, например, 101102=10110=268, 10111002=1011100=5C16. Числа из восьмеричной или шестнадцатеричной СС в двоичную переводятся по обратному правилу: один символ «старой» СС заменяется группой разрядов «новой» СС в количестве, равном показателю степени «новой» СС, например, 4728=100111010=1001110102, B516=10110101=101101012. Как видим, если основа одной СС равняется некоторой степени другой, то перевод очень простой. В противном случае пользуются общими правилами перевода числа из одной позиционной СС в другую (чаще всего при переводе из двоичной, восьмеричной и шестнадцатеричной СС в десятичную, и наоборот). 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
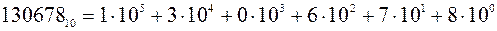 .
.