
|
|
Методы количественной невидимости
Рис. 6.19. Контурная линия Здесь вводится понятие количественной невидимости, как количество граней, закрывающих вершину (точку). Если количественная невидимость равна нулю, то точка видима. Количественная невидимость точек ребра при прохождении так называемой контурной линии может изменяться. Берется какая-нибудь вершина и прослеживается изменение количественной невидимости вдоль каждого из ребер, выходящих из этой вершины. Эти ребра проверяются на прохождение позади контурной линии. Где количественная невидимость равна нулю, ребро сразу рисуется. Если не равно нулю, то проверяется количественная невидимость для всех ребер, выходящих из новой вершины, и. т. д. Этот алгоритм более эффективен, чем алгоритм Робертса, так как количество ребер, входящих в контурную линию, намного меньше общего числа ребер. Методы двоичного разбиения пространства. Плоскости, как обычно, будут задаваться с помощью вектора нормали
Построение плоскостей и дерева в данном случае осуществляется "вручную". Для эффективности работы алгоритма надо стремиться к тому, чтобы дерево было сбалансированным. Если какие-то грани не удается отделить, то их пересекают плоскостями и рисуют как два объекта. Способ определения, по какую сторону плоскости находится наблюдатель, а по какую - грань, очень прост. Параметр плоскости Методы решения задач загораживания Метод переборного типа.(«грубой силы»). В алгоритмах переборного типа, как правило, рассматривается каждое ребро, принадлежащее каждому из объектов сцены, и анализируется его взаимное расположение со всеми гранями каждого из объектов, составляющих сцену. При этом возможны следующие ситуации: Временная сложность алгоритмов такого типа пропорциональна произведению количества ребер и количества граней в сцене. Никакие дополнительные свойства изображаемых объектов не учитываются. Метод Z-буфера. Другим методом «грубой силы» является метод Z-буфера, который весьма удобен для аппаратной реализации ввиду простоты алгоритма и используемого в нем набора операций. Временные характеристики этого метода линейно зависят от количества точек растра и «глубинной сложности сцены», т.е. усредненного числа граней, взаимно закрывающих друг друга. Для реализации метода используются две области памяти: буфер глубины (Z-буфер) и буфер кадра (хранящий информацию о состоянии пикселов экрана компьютера). Буфер длины используется для хранения координаты Z (глубины) каждого видимого на данной стадии анализа изображения пиксела картинной плоскости. В буфере кадра запоминаются атрибуты (интенсивность и цвет) соответствующего пикселя. Формально описание метода таково. Предположим, что сцена представлена в виде объединения многоугольников (возможно, пересекающихся). Построим ортогональную проекцию сцены на картинную плоскость Предполагается следующая последовательность шагов: 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|

 и расстояния до начала координат
и расстояния до начала координат 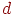 (с точностью до знака). Пусть изображаемая сцена состоит из набора непересекающихся граней
(с точностью до знака). Пусть изображаемая сцена состоит из набора непересекающихся граней  (они могут иметь общие прямолинейные участки границы). Проведем плоскость
(они могут иметь общие прямолинейные участки границы). Проведем плоскость  , разбивающую все пространство на два полупространства, в одном из которых находится наблюдатель. Предположим, что плоскость при этом не пересекает ни одну из граней (но может содержать участок ее границы). Тогда грани, находящиеся в одном полупространстве с наблюдателем, могут заслонять от него часть граней из второго полупространства, но не наоборот. Это означает, что они должны изображаться позже. Разобьем плоскостью
, разбивающую все пространство на два полупространства, в одном из которых находится наблюдатель. Предположим, что плоскость при этом не пересекает ни одну из граней (но может содержать участок ее границы). Тогда грани, находящиеся в одном полупространстве с наблюдателем, могут заслонять от него часть граней из второго полупространства, но не наоборот. Это означает, что они должны изображаться позже. Разобьем плоскостью 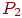 второе полупространство и снова определим, какая группа граней из него должна изображаться раньше. Продолжая этот процесс до того уровня, когда все пространство будет разбито плоскостями на секции, в каждой из которых будет находиться только одна грань, мы получим упорядоченный набор граней. Этот порядок можно изобразить в виде двоичного дерева. В контексте рассматриваемого алгоритма это дерево представляет собой структуру данных
второе полупространство и снова определим, какая группа граней из него должна изображаться раньше. Продолжая этот процесс до того уровня, когда все пространство будет разбито плоскостями на секции, в каждой из которых будет находиться только одна грань, мы получим упорядоченный набор граней. Этот порядок можно изобразить в виде двоичного дерева. В контексте рассматриваемого алгоритма это дерево представляет собой структуру данных  , элементами которой являются указатель на грань изображаемой сцены, плоскость, отделяющая эту грань, указатели на левое и правое поддерево
, элементами которой являются указатель на грань изображаемой сцены, плоскость, отделяющая эту грань, указатели на левое и правое поддерево  и
и  . Такой элемент называется узлом дерева.
. Такой элемент называется узлом дерева.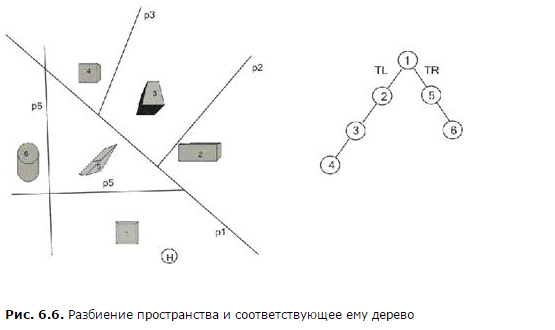
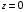 .
.