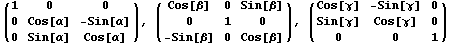Матрицы аффинных преобразований в пространстве.
Мы будем далее предполагать, что в пространстве задана декартова система координат  . В такой системе координат точки задаются тройками чисел . В такой системе координат точки задаются тройками чисел  , которые нам будет удобно записывать в виде столбцов вида , которые нам будет удобно записывать в виде столбцов вида  . .
Нас будут интересовать так называемыеиаффинные преобразования пространства. Это такие преобразования, при которых все прямые преобразуются снова в прямые. Оказывается, что все такие преобразования можно записать формулами вида

где  - координаты исходной точки; те же буквы со звёздочкой наверху обозначают координаты точки, которая получается в результате преобразования. Для компактной записи этих формул весьма полезно использовать матричные обозначения. Именно, определим матрицу и три столбца следующим образом: - координаты исходной точки; те же буквы со звёздочкой наверху обозначают координаты точки, которая получается в результате преобразования. Для компактной записи этих формул весьма полезно использовать матричные обозначения. Именно, определим матрицу и три столбца следующим образом:
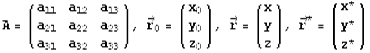
Тогда приведённое выше преобразование можно записать в форме простого матричного равенства  . В дальнейшем мы все преобразования будем записывать в такой форме, указывая при необходимости вид матрицы . В дальнейшем мы все преобразования будем записывать в такой форме, указывая при необходимости вид матрицы  . .
Самым простым преобразованием такого вида является параллельный сдвиг на вектор  , который определяется формулой , который определяется формулой  . Матрица . Матрица  в этом случае совпадает с единичной матрицей в этом случае совпадает с единичной матрицей 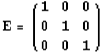 . .
Сдвиг на ненулевой вектор не имеет неподвижных точек.
В общем случае можно определить, имеет ли преобразование неподвижные точки, решая систему уравнений  , где , где  - единичная матрица. Заметим, что если матрица - единичная матрица. Заметим, что если матрица  невырожденная, то есть, её определитель не равен невырожденная, то есть, её определитель не равен  , то эта система имеет единственное решение , то эта система имеет единственное решение  , так что преобразование имеет единственную неподвижную точку. , так что преобразование имеет единственную неподвижную точку.
Если вектор  нулевой, то преобразование имеет вид нулевой, то преобразование имеет вид 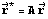 . Такое преобразование оставляет неподвижным начало координат . Такое преобразование оставляет неподвижным начало координат  . .
Если мы уже нашли преобразование нужного вида (с матрицей  ), оставляющее неподвижным начало координат, то очень легко найти преобразование такого же вида, оставляющее неподвижной заданную точку ), оставляющее неподвижным начало координат, то очень легко найти преобразование такого же вида, оставляющее неподвижной заданную точку  . Такое преобразование будет иметь вид . Такое преобразование будет иметь вид 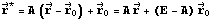 . Поэтому в дальнейшем мы будем ограничиваться преобразованиями, оставляющими неподвижным именно начало кординат, то есть, преобразованиями вида . Поэтому в дальнейшем мы будем ограничиваться преобразованиями, оставляющими неподвижным именно начало кординат, то есть, преобразованиями вида 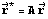 . .
Другой простейший тип преобразований - растяжения (сжатия) вдоль прямой. Растяжение вдоль оси  в в  раз задаётся, соответственно, матрицей раз задаётся, соответственно, матрицей
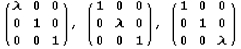
(при  получается сжатие). Растяжение одновременно по всем осям (вообще говоря, в разное число раз) задаётся матрицей получается сжатие). Растяжение одновременно по всем осям (вообще говоря, в разное число раз) задаётся матрицей

Если все диагональные элементы в этой матрице одинаковые, то получается равномерное растяжение (сжатие), то есть, преобразование подобия.
Симметрии относительно плоскостей  , осей , осей  и точки и точки 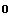 (начала координат) задаются матрицами (начала координат) задаются матрицами
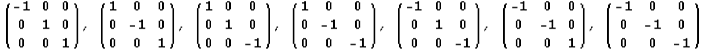
Симметрии относительно произвольных плоскостей и прямых можно получить по той же формуле, что и растяжения, взяв в качестве  нужную комбинацию чисел нужную комбинацию чисел  и и 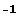 . Однако если мы хотим, чтобы полученное преобразование было действительно симметрией нужного вида, векторы . Однако если мы хотим, чтобы полученное преобразование было действительно симметрией нужного вида, векторы  , для которых , для которых 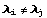 , должны быть перпендикулярны, то есть, их скалярное произведение должно быть равно , должны быть перпендикулярны, то есть, их скалярное произведение должно быть равно  : :  . .
При отыскании нужных векторов полезно иметь в виду, что вектор с координатами  перпендикулярен плоскости перпендикулярен плоскости  . .
В частности, матрица симметрии относительно плоскости 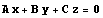 имеет вид имеет вид

Более сложным классом преобразований являются движения, то есть, преобразования, сохраняющие расстояния между точками. Матрица  , определяющая движение, является ортогональной, то есть, удовлетворяет условию , определяющая движение, является ортогональной, то есть, удовлетворяет условию  . Это означает, что обратная матрица должна совпадать с транспонированной. . Это означает, что обратная матрица должна совпадать с транспонированной.
Все движения можно разбить на две группы: собственные движения, которые являются комбинациями вращений и сдвигов и характеризуются тем, что определитель матрицы  равен равен  , и несобственные движения, которые включают дополнительно симметрию относительно плоскости или точки и характеризуются тем, что определитель матрицы , и несобственные движения, которые включают дополнительно симметрию относительно плоскости или точки и характеризуются тем, что определитель матрицы  равен равен 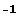 . .
Заметим, что симметрию относительно прямой можно рассматривать как вращение вокруг этой прямой на угол 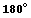 , так что такие симметрии являются собственными движениями. , так что такие симметрии являются собственными движениями.
Собственные движения, имеющие неподвижную точку, называются вращениями. Как мы и договорились, будем предполагать, что эта неподвижная точка совпадает с началом координат 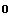 . .
Самый простой случай - поворот вокруг оси координат на заданный угол. Матрица поворота на угол  вокруг оси вокруг оси  соответственно имеет следующий вид: соответственно имеет следующий вид:
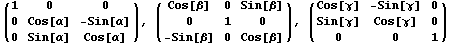
Не нашли, что искали? Воспользуйтесь поиском по сайту:
©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|


 . В такой системе координат точки задаются тройками чисел
. В такой системе координат точки задаются тройками чисел  , которые нам будет удобно записывать в виде столбцов вида
, которые нам будет удобно записывать в виде столбцов вида  .
.
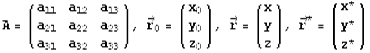
 . В дальнейшем мы все преобразования будем записывать в такой форме, указывая при необходимости вид матрицы
. В дальнейшем мы все преобразования будем записывать в такой форме, указывая при необходимости вид матрицы  .
. , который определяется формулой
, который определяется формулой  . Матрица
. Матрица 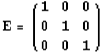 .
. , где
, где  - единичная матрица. Заметим, что если матрица
- единичная матрица. Заметим, что если матрица  невырожденная, то есть, её определитель не равен
невырожденная, то есть, её определитель не равен  , то эта система имеет единственное решение
, то эта система имеет единственное решение  , так что преобразование имеет единственную неподвижную точку.
, так что преобразование имеет единственную неподвижную точку.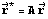 . Такое преобразование оставляет неподвижным начало координат
. Такое преобразование оставляет неподвижным начало координат  .
.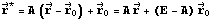 . Поэтому в дальнейшем мы будем ограничиваться преобразованиями, оставляющими неподвижным именно начало кординат, то есть, преобразованиями вида
. Поэтому в дальнейшем мы будем ограничиваться преобразованиями, оставляющими неподвижным именно начало кординат, то есть, преобразованиями вида  в
в  раз задаётся, соответственно, матрицей
раз задаётся, соответственно, матрицей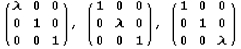
 получается сжатие). Растяжение одновременно по всем осям (вообще говоря, в разное число раз) задаётся матрицей
получается сжатие). Растяжение одновременно по всем осям (вообще говоря, в разное число раз) задаётся матрицей
 , осей
, осей 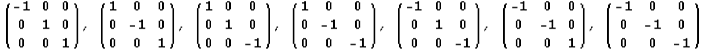
 нужную комбинацию чисел
нужную комбинацию чисел  и
и 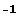 . Однако если мы хотим, чтобы полученное преобразование было действительно симметрией нужного вида, векторы
. Однако если мы хотим, чтобы полученное преобразование было действительно симметрией нужного вида, векторы  , для которых
, для которых 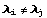 , должны быть перпендикулярны, то есть, их скалярное произведение должно быть равно
, должны быть перпендикулярны, то есть, их скалярное произведение должно быть равно  .
. перпендикулярен плоскости
перпендикулярен плоскости  .
.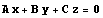 имеет вид
имеет вид
 . Это означает, что обратная матрица должна совпадать с транспонированной.
. Это означает, что обратная матрица должна совпадать с транспонированной.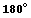 , так что такие симметрии являются собственными движениями.
, так что такие симметрии являются собственными движениями. вокруг оси
вокруг оси