|
|
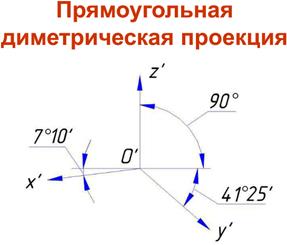
Алгоритм Брезенхейма для развертки отрезкаАксонометрическая проекция. Виды аксонометрических проекций. Аксонометрическое изображение должно отвечать двум основным требованиям: · быть наглядным, то есть таким, чтобы по нему можно было представить форму изображенного объекта и его частей; · быть обратимым (метрически определенным), то есть таким, чтобы по нему можно было изготовить изображенный объект. Аксонометрической проекцией называют изображение, полученное при параллельном проецировании на какую-либо плоскость предмета вместе с осями прямоугольных координат, к которым он отнесен в пространстве. Рассмотрим сущность метода аксонометрии. Пусть в пространстве находится каркас куба со стороной ребра е, принимаемой за натуральную масштабную единицу (рис. 1). Куб вместе с координатными осями Х, У, Z спроецируем лучами, параллельными направлению проецирования s, на некоторую плоскость П', расположенную произвольно относительно граней куба. Полученное изображение называют аксонометрическим (или аксонометрией).
Основными элементами проекционного аппарата аксонометрии являются: · s – направление проецирования и проецирующие лучи; · П'– аксонометрическая плоскость проекций (или картинная плоскость); · Х', У', Z'– аксонометрические проекции координатных осей; · ех', еу', еz' – единичные аксонометрические масштабные отрезки. При образовании аксонометрического изображения координатные отрезки – отрезки вдоль Отношения аксонометрических координатных отрезков к их натуральной величине называют коэффициентами искаженияи обозначают: по оси Х: Обратимость аксонометрического чертежа обеспечивается указанием на нем коэффициентов искажения. Угол между направлением проецирования и плоскостью аксонометрических проекций может изменяться, соответственно будут изменяться и коэффициенты искажения, так как они находятся в определенной зависимости, которая выявляется формулой, называемой основной формулой аксонометрии:
где - угол между направлением проецирования и аксонометрической плоскостью проекций.
Алгоритм Брезенхейма для развертки отрезка При построении растрового образа отрезка необходимо, прежде всего, установить критерии "хорошей" аппроксимации. Первое требование состоит в том, что отрезок должен начинаться и кончаться в заданных точках и при этом выглядеть сплошным и прямым (при достаточно высоком разрешении дисплея этого можно добиться). Кроме того, яркость вдоль отрезка должна быть одинаковой и не зависеть от наклона отрезка и его длины. Это требование выполнить сложнее, поскольку горизонтальные и вертикальные отрезки всегда будут ярче наклонных, а постоянная яркость вдоль отрезка опять же достигается на вертикальных, горизонтальных и наклоненных под углом в 45
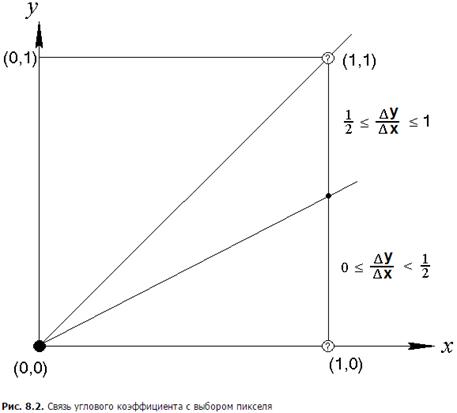
На рис. 8.2 это иллюстрируется для отрезка с угловым коэффициентом, лежащим в диапазоне от нуля до единицы. Из рисунка можно заметить, что если угловой коэффициент На рис. 8.3 показано, каким образом строятся точки растра для отрезка с тангенсом угла наклона На рис. 8.5 приведена блок-схема алгоритма для случая
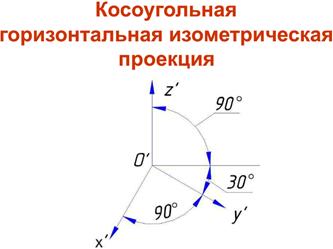
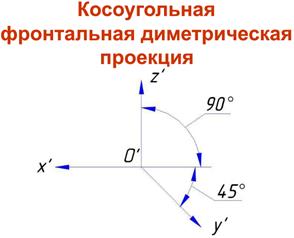
Косоугольные проекции 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
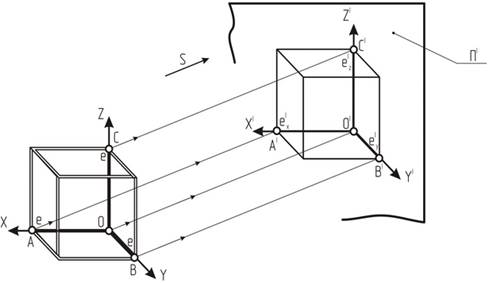
 координатных осей (е), будут проецироваться на плоскость аксонометрических проекций искаженно – в аксонометрические координатные отрезки ех', еу', еz' .
координатных осей (е), будут проецироваться на плоскость аксонометрических проекций искаженно – в аксонометрические координатные отрезки ех', еу', еz' .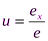 ; по осиУ:
; по осиУ: 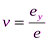 ; по оси Z:
; по оси Z: 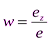 .
.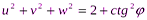 , (1)
, (1)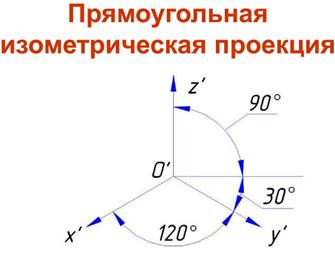

 линиях. И, наконец, алгоритм должен работать быстро. Для этого необходимо по возможности исключить операции с вещественными числами. С целью ускорения работы алгоритма можно также реализовать его на аппаратном уровне.
линиях. И, наконец, алгоритм должен работать быстро. Для этого необходимо по возможности исключить операции с вещественными числами. С целью ускорения работы алгоритма можно также реализовать его на аппаратном уровне.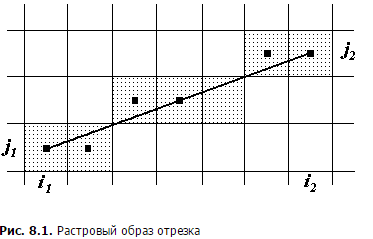
 , то при выходе из точки
, то при выходе из точки  пересечение с прямой
пересечение с прямой 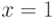 будет ближе к прямой
будет ближе к прямой  , чем к прямой
, чем к прямой  . Следовательно, точка растра
. Следовательно, точка растра  лучше аппроксимирует прохождение отрезка, чем точка
лучше аппроксимирует прохождение отрезка, чем точка 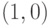 . При
. При 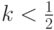 верно обратное.
верно обратное.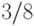 , а на рис. 8.4 - графиксмещения. В начале построения смещение полагается равным
, а на рис. 8.4 - графиксмещения. В начале построения смещение полагается равным  , а затем на каждом шаге оно наращивается на величину
, а затем на каждом шаге оно наращивается на величину 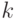 , и если при этом вертикальная координата точки растра увеличивается на единицу, то смещение в свою очередь уменьшается на единицу.
, и если при этом вертикальная координата точки растра увеличивается на единицу, то смещение в свою очередь уменьшается на единицу.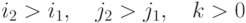 . Нетрудно понять, как от этого алгоритма перейти к целочисленному: достаточно вместо величины смещения
. Нетрудно понять, как от этого алгоритма перейти к целочисленному: достаточно вместо величины смещения  перейти к величине
перейти к величине 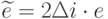 .
.