|
|
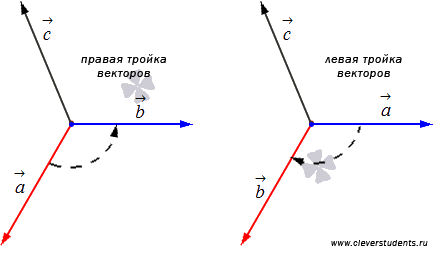
Векторное произведение, его свойства, вычисление.Векторным произведением вектора a на вектор b называется вектор с=a x b. который определяется следующими тремя условиями: 1. |a x b|=|a|*|b|*sinφ 2. a|_c, b|_c вектор с ортогонален векторам a и b 3. вектор с направлен так, что векторы a,b,c образуют правую тройку. (если кратчайший поворот вектора а к вектору b осуществляется против часовой стрелки – правая тройка. i,j,k – правая тройка.
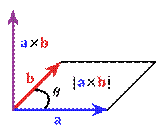
Геометрические свойства: 1. Если a||b ↔ a x b=0 (необходимое и достаточное условие коллинеарности) sinφ=0 2. Если a и b приведены к общему началу, то S=|a|*|b|*sinφ=|a x b| (площадь параллелограмма) Sтр=1/2*Sпар=1/2*|a x b|
Алгебраические свойства: 1. а x b= -b x a (меняется направленность тройки) 2. Сочетательный закон по отношению к умножению на скаляр (λa) x b= λ(a x b) (a x λb)= λ(a x b) 3. Распределительный закон относительно умножения на сумму векторов a x (b+c) = a x b + a x c (b+c) x a= b x c + c x a 4. a x a =0 Выражение векторного произведения через координаты перемножаемых векторов в декартовой системе координат. Теорема: Пусть векторы а и b заданы своими декартовыми координатами: a={x1,y1,z1} b={x2,y2,z2}
|i j k| тогда a x b=|x1 y1 z1|={ |y1 z1|, - |x1 z1|, |x1 y1|} |x2 y2 z2| |y2 z2| |x2 z2|, |x2 y2| Док-во: Составим таблицу векторного умножения базисных векторов. i x i=0 j x i =-k k x i =j i x j=k j x j =0 k x j =-i i x k=-j j x k= i k x k=0 Воспользуемся представлением a и b в декартовой системе координат: а=x1*i+y1*j+z1*k b=x2*i+y2*j+z2*k a x b= (x1*i+y1*j+z1*k)x(x2*i+y2*j+z2*k)=…=|y1 z1|i - |x1 z1|j + |x1 y1|k |y2 z2| |x2 z2| |x2 y2| Смешанное произведение трех векторов, его свойства, геометрический смысл, вычисление. Определение: (a x b)c – векторно-скалярное или смешанное произведение векторов. 1. Компланарность векторов a,b,c – принадлежность к одой плоскости или параллельным плоскостям. (можно снести на одну плоскость) 2. Упорядоченная тройка векторов, такая тройка векторов о которых известно, какой из них является первым, вторым и третьим. 3. Правая и левая тройка векторов.
y- вектор b z- вектор c (a,b,c) (b,c,a) (c,a,b) правые (b,a,c) (a,c,b) (c,b,a) левые Теорема 1: Смешанное произведение векторов (a x b)c равно объему параллелепипеда ( построенного на векторах a,b,c) взятому со знаком +, если тройка правая, и – если тройка левая. Док-во: Если a,b,c компланарны, то (a x b)c =0 (очевидно) (a x b) |_c Пусть a не коллинеарно b тогда a x b=Se (S- площадь параллелограмма) (a,b , a x b,) – правая тройка Se*c=S*|e|*прeс=S*прec=S*H=V (если a,b,c – правая) Если левая, то прec=-H, (a x b)c=-V Следствия: 1. (a x b)c=(b x c)a=a(b x c)=abc 2. Компланарность abc=0 Теорема 2: Пусть a={x1,y1,z1} b={x2,y2,z2} c={x1,y1,z1} – векторы заданные декартовыми координатами. Тогда |x1 y1 z1| abc=|x2 y2 z2| |x3 y3 z3| Док-во: abc=(a x b)c ↔ a x b=| i j k|=(y1z2-z1y2)i-(x1z2-x2z1)j+(x1y2-x2y1)k |x1 y1 z1| |x2 y2 z2| abc – скалярное произведение (a x b) и с ↔ (a x b)c=x3(y1z2-z1y2)-y3(x1z2-x2z1)+z3(x1y2-x2y1)=| x1 y1 z1 | |x2 y2 z2| |x3 y3 z3|
3.1. Прямая линия на плоскости. Различные уравнения прямой. Угол между прямыми, условия параллельности и перпендикулярности прямых на плоскости. Нормальный и направляющий вектор прямой Нормальный вектор прямой – любой ненулевой вектор, ортогональный этой прямой. n |_ L Направляющий вектор прямой называется любой ненулевой вектор, параллельный этой прямой. Определение: Уравнение данной линии ( в выбранной системе координат) называется уравнением вида F(x,y)=0. Линия – геометрическое место точек удовлетворяющее этому уравнению. Линия определяется уравнением y=f(x) – график функции f(x). Векторное уравнение прямой на плоскости.
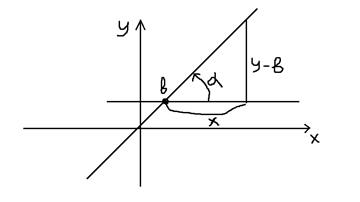
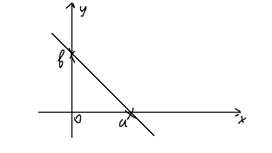
Составим общее векторное уравнение. Очевидно, что MM0 |_ n, откуда скалярное произведение M0M*n=0, поскольку M0M=r-r0, то (r-r0)n=0, или rn-r0n=0. Обозначив C=-r0n, получим rn+C=0 (общее векторное уравнение) Составим векторное параметрическое уравнение: Воспользуемся тем, что M0M||q или (r-r0)||q, откуда r-r0=tq (векторное параметрическое уравнение прямой а плоскости) Общее уравнение прямой на плоскости: Теорема: В декартовой системе координат каждая прямая определяется уравнением первой степени. Док-во: (y-b)/x=k=tgα (y-b)/x=k → y-b=kx → kx-y+b=0 уравнение первой степени. Если α=90 → x=a также уравнение первой степени. Общее уравнение прямой на плоскости: Ax+By+C=0 Неполное уравнение первой степени: а) С=0 → Ax+By=0 – уравнение прямой проходящей через начало координат. б) A=0 → By+C=0 → y=-C/B B≠0 (прямая параллельная оси Ох) в) B=0 → Ax+C=0 → x=-C/A (прямая параллельная оси Ох) Уравнение прямой в отрезках: Ax+By+C=0 → Ax+By=-C → -Ax/C-By/C=1 → x/-CA+y/-CB=1 → x/a+y/b=1 (2) (2) уравнение прямой в отрезках.
a,b – отрезки, отсекаемые прямой на координатных осях ( не длины отрезков) 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 x- вектор а
x- вектор а