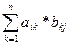|
|
Определители второго и третьего порядка. Свойства определителей.Определитель второго порядка находится как detA=а11*а22-а12*а21 Определитель третьего порядка можно найти: 1) вычеркиванием i-ой строки и j-го столбца 2) правило треугольников Свойства определителей: 1) А=(aij)n A’ =(aij)n – транспонированная detA=detA’ (доказательство примером с а11 а12 а13) 2) При перестановке местами двух строк (столбцов) определитель не меняет величины, знак меняется на противоположенный. (доказательство примером с а11 а12 а13) 3) Линейное свойство определителя. Будем говорить, что некоторая строка (а1, … , аn) если линейная комбинация строк (b1,…,bn), (C1,…,Cn), … , если существует λ, μ, υ,… такие что, aj=λ*bj+μ*cj+… (j=1, … , n) Пусть в определителе n-го порядка A некоторая i-ая строка (а1, а12, … ,а1n) является линейной комбинацией двух строк (b1, … ,bn), (C1, … , Cn) : aij=λbj+μcj (j=1,…,n) Свойство: detA=λ*detB+μ*detC аналогично для столбцов. (detB – определитель матрицы, с i-ой строкой (b1, … ,bn) detC – определитель матрицы с i-ой строкой (С1, …, Сn) Доказательство очевидно по формуле:
Следствия: 1) Определитель с двумя одинаковыми строками (столбцами) равен нулю (доказательство очевидно) 2) Умножение всех элементов стоки (столбца) на постоянный множитель равносильно умножению на этот множитель 3) Если все элементы строки (столбца) равны нулю, то detA=0 4) Если элементы двух строк (столбцов) пропорциональны, то detA=0 (из 1 и 2 следствия) 5)Если к элементам некоторой строки (столбца) добавить элементы другой строки (столбца) умноженные на произвольную постоянную, то при этом определитель не изменяется (из 3 свойства). Можно прибавить линейную комбинацию строк (столбцов) 1.2. Свойства определителей. Определители 2-го порядка. Формулы Крамера. Формулы Крамера. a11x1+a12x2+…+a1nxn=b1 a21x1+a22x2+…+a2nXn=b2 … an1x1+an2x2+…+annXn=Bn |a11 a12 … a1n| ∆=detA=|a21 a22 … a2n|≠0 |an1 an2 … ann| |a11x1 a12…a1n| |a11x1 a12x2…a1nxn| |b1 a22 … a1n| ∆*x1= |a21x1 a22…a2n|=|a21x1 a22x2…a2nxn|=|b2 a12 … a2n|= ∆1 |an1x1 an2…ann| |an1x1 an2x2…annxn| |b3 an2 … ann| Добавим к первому столбцу второй умноженный на х2, третий на х3, n-ый на хn. Получим: |b1 a22 … a1n| |b2 a12 … a2n|= ∆1 |b3 an2 … ann| x1=∆1/∆, xj=∆j/∆ - Формула Крамера аналогично для остальных Применяются только в случае, когда число переменных совпадает с числом уравнений. Необходимо, чтобы все уравнения были линейно независимы, т.е. ни одно уравнение не являлось бы линейной комбинацией остальных, для этого необходимо, чтобы detA≠0
Где
1. Если определитель системы 2. Если определитель системы 3. Если 1.3. Матрицы. Виды матриц. Линейные операции над матрицами. Произведение матриц. Матрица – набор числе записанных в таблице. (m x n) матрица (m строк, n столбцов) Бывает квадратной, прямоугольной, матрица-строка, матрица-столбец, единичная матрица, нулевая матрица, верхне-треугольная матрица, нижне-треугольная матрица, диагональная, транспонированная, др. Операции над матрицами: 1. Равенство матриц. А=В Aij=Bij (размерности совпадают) 2. Сложение А+В=С Cij=Aij+Bij i=1, … , m j=1, … , n a11+b11 a12+b12 a13+b13… Свойства: а) переместительный закон А+В=В+А б) сочетательный закон (А+В)+С=А+(В+С) 3) Умножение матрицы на число С=λА Свойства: а)λ(A+B)=λA+λB б)(λ+μ)А=μА+λА в)(λμ)А=λ(μА) 4. Разность матриц А-В=А+(-1)*В С=А-В Сij=Aij-Bij (i=1, … ,m j=1, … ,n) 5. Перемножение матриц А=(aij) i=1, … ,m j=1, …,n B= (bij) i=1, … ,n j=1, … ,k C=A*B=(Cij) i=1,…,m j=,…,p Cij= Свойства: а) АВ≠ВА б) (АВ)С= А(ВС) в) (А+В)С=АС+ВС det(AB)=detA*detB 1.4. Обратная матрица и ее вычисление методом Крамера (методом присоединенной матрицы). Метод элементарных преобразований вычисления обратной матрицы. Обратная матрица 1. Понятие обратной матрицы Правая обратная матрица "В" : A*B=E; Левая обратная матрица "С" : C*A=E; Теорема 1. Если В и С существ., то В=С. Доказ: А*В=Е; CA=E; C=CE; C=C(AB)=(CA)B=EB=B;
Матрица А-1 называется обратной по отношению к квадратной матрице А, если она перестановочна с ней и А*А-1=А-1А=Е Матрицы А и А-1 взаимно обратимы, т.е. (А-1)-1=А Обратную матрицу может иметь только квадратная матрица. Теорема 2. Для того, чтобы для квадратный матриц А существ.,правая и левая обратные матрицы, необходимо и достаточно, чтобы ее определитель был отличен от нуля. Доказ: Необходимость Пусть хотя бы одно из В, С сущ.: CA=E; det(CA)=detC*detA=1; detC=1/detA; detAне равен 0. Если обратная матрица существует, то она единственная. А=(3 7 А-1= ( 5 -7 2 5 ) -2 3) Метод присоединенной матрицы: 1. Вычислить определитель матрицы А 2. Вычислить все алгебраические дополнения Аij и составить из них матрицу алгебраических дополнений.( Аij=(-1)j+i*(минор)) 3. Получить присоединенную матрицу Аji, путем транспонирования матрицы алгебраических дополнений. 4. Разделить матрицу Аij на определить detA: + дается в виде формулы - вычисления громоздкие Метод элементарных преобразований: К элементарным преобразованиям относится: 1. Перестановка двух строк (столбцов) 2. Умножение всех элементов какой-либо строки (столбца) на ненулевой сомножитель. 3. Прибавление к элементам какой-либо строки (столбца) элементов другой строки (столбца) умноженных на один и тот же сомножитель (можно линейные комбинации других строк (столбцов)) Теорема: Пусть последовательность элементарных преобразований только над строками матрица А (detA≠0) приводят ее к единичной матрице Е. Тогда те же элементарные преобразования приводят единичную матрицу Е к обратной матрице А-1 Аналогично для столбцов. Правило вычисления обратной матрицы: 1. Записать рядом две матрицы: А|Е 2. Получить верхне-треугольную (нижне-треугольную) матрицу А 3. Получить в главной диагонали преобразуемой матрицы единицы. Тогда на месте исходной единичной матрицы Е будет находиться обратная матрица. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
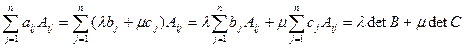
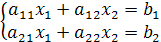




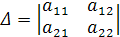
 , тогда система имеет единственное решение, определяемое формулами Крамера.
, тогда система имеет единственное решение, определяемое формулами Крамера. . Если хотя бы один из
. Если хотя бы один из  и
и  не равен нулю, тогда система не имеет решений.
не равен нулю, тогда система не имеет решений. ,
,  и
и  то одно уравнение есть следствие другого, система сводится к одному уравнению с двумя неизвестными, имеющая бесконечное множество решений.
то одно уравнение есть следствие другого, система сводится к одному уравнению с двумя неизвестными, имеющая бесконечное множество решений.