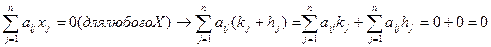Системы линейных алгебраических уравнений. Метод Гаусса. Решение систем линейных алгебраических уравнений с помощью обратной матрицы.

Системой линейных уравнений называется система уравнений вида:

a11x1+ a12x2 + … +a1nXn =b1

a21x1+ a22x2 + … +a2nXn =b2

………….

am1x1 am2x2 + … +amnXn=bm

где x1,x2,… неизвестные, a_ij коэффициент при неизвестных;

b1,b2,..bm свободные члены; m – число уравнений; n – число неизестных;

i=1,2,…,m j=1,2,…,n

Уравнение называется линейным, т.к. неизвестные входят во все уравнения в первой степени.

Решение СЛАУ: Совокупность чисел L1,L2,...Ln называется решением системы, если после подстановки x1=L1, x2=L2, xn=Ln каждое уравнение системы превращается в тождество.

Метод Гаусса (последовательное исключение) решения СЛАУ.

Матрица записывается как (A|B)

1. Прямой ход (преобразование исходной матрицы в верхне-треугольную.

2. Получение единичной диагонали.

И нахождение неизвестных начиная снизу.

+является универсальным, охватывает все возможные случаи в решении

+является экономичным, по сравнению с методом Крамера

Решение СЛАУ с помощью обратной матрицы:

Квадратная матрица и detA≠0. В этом случае можно найти решение с помощью обратной матрицы, т.к. detA≠0 и А^-1 существует.

Умножим обе части матричного уравнения АХ=В на матрицу A^-1

Слева: АХА^-1= А^-1В, откуда Х= А^-1В

XA=B→XAA^-1=BA^-1 →X=BA^-1

A1XA2=B → X=A1^-1BA2^-1

1.7. Исследование систем линейных алгебраических уравнений. Теорема Кронекера-Капелли. Однородные системы линейных алгебраических урав­нений.

Исследовать СЛАУ – это значит до нахождения решения ответить на два вопроса:

1) совместна ли она

2) определена или неопределена система.

Если система не имеет ни одного решения, то она называется несовместной.

Если у системы есть хотя бы 1 решение, то она называется совместной.

Совместная система называется определенной, если она имеет единственное решение.

Неопределенной если решений больше 1.

Теорема Кронекера-Капелли:

a11x1+a12x2+…+a1nxn=b1

a21x1+a22x2+…+a2nxn=b2

…..

as1x1+as2x2+…+asnXn=bs

(1) s≠n

СЛАУ совместна тогда и только тогда, когда r(A)=r(A|B)

Док-во:

а) необходимость

Пусть {k1,…,kn} – набор чисел – решение (1)

a11 a12 a1n b1

k1*(a21)+ k2*(a22)+ kn*(a2n)+ =(b2)

as1 as2 asn bs

→столбец (b1,…,bs)^T линейная комбинация столбцов матрицы А→ (b1,…,bs)^T линейная комбинация базисных(базовых) столбцов матрицы А→r(A)=r(A|B)

б) достаточность

Пусть r(A)=r(A|B)=r →

a11 a12 a12+1 b1

k`1*(a21)+ k`2*(a22)+ 0*(a22+1)+…+0() = (b2)

as1 as2 asr+1 bs

Таким образом мы получим по крайней мере одно решение.

x` (черта)={k'1,k'2,0,...0}

Система линейных однородных уравнений:

a11x1+a12x2+…+a1nXn=0

a21x2+a22x2+…+a2nXn=0

…

as1x1+as2x2+…+asnXn=0

(4)
Из т. К-К следует, что (4) всегда совместна, т.к. всегда r(A)=r(A|B) (столбец правых частей нулевой)

Справедливы утверждения:

1. Если r=n (S>=n), то нулевое решение (4) будет единственным решением (4)

2. Если r<n, то система (4) обладает ненулевыми решениями (часть переменных становиться свободными и образуют ненулевую правую часть)

3. Система n линейных однородных уравнений тогда и только тогда имеет ненулевые решения, когда det(A)=0

4. Если в однородной системе (4) число уравнений S<n, то (4) имеет ненулевые решения.

Свойства решений однородной СЛАУ:

1. Если k’={k1,k2,…,kn} – решение (4), то k``=βk`={βk1,βk2,…,βkn} –решение (4), β – произвольная константа.

2. Пусть k` и h` - два решения (4), тогда k`+h`={k1+h1,k2+h2,…,kn+hn} –решение (4)

Всякая линейная комбинация решений (4) также решение (4)

2.1. Геометрический вектор. Равенство векторов, коллинеарность, компла­нарность. Линейные операции над векторами.

Геометрический вектор – это отрезок имеющий начало и конец.

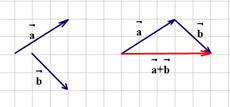
А-начало

В-конец

Модуль вектора – это число, равное расстоянию между началом и концом.

Нулевой вектор – это вектор, начало и конец которого совпадают.

Единичный вектор – вектор, модуль которого равен единице.

Векторные и скалярные величины:

Векторнаявеличина – величина, задаваемая с помощью вектора. Характеризуется числом и модулем.

Скалярная величина – величина, задаваемая только числом.

Равенство векторов:

Два вектора равны, если лежат на параллельных прямых или на одной прямой, сонаправлены и имеют равные модули.

Два вектора равные третьему, равны между собой.

Свободный вектор – можно переносить параллельно самому себе, помещая его начало в любую точку пространства. При этом вектор остается равный самому себе.

Коллинеарность и компланарность векторов

Два вектора коллинеарны, если они расположены на одной или параллельных прямых.

A||b

Если а- ненулевой вектор, то для любого коллинеарного вектора b существует единственное число λ, такое что b=λa

Если λ>0 - сонаправлены, λ<0 - направлены противоположно.

Три вектора называются компланарными, если они расположены в параллельных плоскостях (если их свести к общему началу, то на одной плоскости)

Линейные операции над векторами:

1.Произведение:

Произведение вектора а на число λ называется вектор b, определенный следующими условиями:

1)модуль вектора b равен произведению модуле сомножителей

|b|=| λ|*|a|

2) векторы a и b коллинеарны

a||b

3) a и b сонаправлены если λ>0, и направлены противоположно, если λ<0

При умножении вектора на ноль получится нулевой вектор с неопределенным направлением.

Сложение

Сложение выполняется по правилу треугольника или параллелепипеда:

Треугольника:

1) конец первого вектора совместить с началом второго.

2) провести вектор из начала первого в конец второго, он и будет равен сумме ветров.

Сложение по правилу треугольников обобщается на сумму нескольких векторов.

Параллелепипеда:

Суммой двух векторов называется вектор, служащий диагональю параллелограмма, построенного на этих векторах как на сторонах.

1) совместить начала суммируемых векторов

2) на суммируемых векторах построить параллелограмм

3)построить вектор на диагонали параллелограмма.

Свойства линейных операций над векторами:

1) переместительный закон сложения

a+b=b+a

2) сочетательный закон

a+b+c=a+(b+c)=(a+b)+c

λaβ= λ(aβ)= (λa)β

3) распределительный зако

λ(a+b)= λa+ λb

(α+β)a=αa+βa

Угол между векторами:

Угол между двумя векторами называется наименьший угол на который нужно повернуть один из векторов до совмещения с другим. ( сначала нужно совместить их начала)

Если угол между векторами прямой, то они ортогональный между собой.

Не нашли, что искали? Воспользуйтесь поиском по сайту: