
|
|
Определение термического КПД циклаТермический КПД цикла определяется как отношение полезно полученной работы в паровой турбине к количеству подведенного тепла в цикле
i′2 = Ср∙t2 = 4,19∙45,8 = 192 кДж/кг Удельный расход пара (расход пара, необходимый для выработки 1 кВт∙ч электроэнергии)
Часовой расход пара D = N∙d = 2500∙2,89 = 7,225 кг/ч. Удельный расход тепла q = d (i1 - i′2) = 2,89∙(3460 – 192) = 9445 кДж/кВт∙ч. Часовой расход тепла Q = q N = 9445∙2500 = 23,61∙106 кДж/ч. Количество охлаждающей воды, необходимой для конденсации пара, определяется из уравнения теплового баланса конденсатора D∙(i2 - i3) = GВ∙CВ∙ΔtВ, где D·(i2 - i3) – количество тепла, отводимого от пара охлаждающей водой до его полной конденсации, GВ∙CВ∙ΔtВ – количество тепла, переданного паром охлаждающей воде:
Ответ: ηt = 38,1%; D=7,225 кг/ч; Q = 23,61∙106 кДж/ч; Gв = 348,87∙103 кг/ч.
Задачи для самостоятельного решения
Задача 3.1.39. Провести термодинамический расчет поршневого двигателя, работающего по циклу Дизеля, при следующих исходных данных. Начальный удельный объем газа, υ1=1,2 м3/кг, степень сжатия, ε=υ1/υ2=12. Начальная температура сжатия, t1 = 25°С. Количество тепла, подводимое в цикле q1 = 900 кДж/кг. Определить параметры состояния (Р, υ, Т, i, и, s) в крайних точках цикла. Энтальпию i и внутреннюю энергию и определить относительно состояния газа при Т0 = 0 К; энтропию определить относительно состояния при условиях T0 = 273,2 К; Р = 0,1 МПа. Построить цикл в Р-υ и T-s координатах. Для каждого процесса определить работу, количество подведенного или отведенного тепла, изменение внутренней энергии, энтальпию и энтропию. Определить работу цикла, количество подведенного и отведенного тепла, термический КПД цикла, сравнить его с КПД цикла Карно, имеющего с рассматриваемым циклом одинаковые максимальные и минимальные температуры.
Рис. 3.1.8. Цикл Дизеля в координатах Р-υ и T-s Рабочее тело - 1 кг воздуха (R = 0,287 кДж/кг∙К; СP = 1,0 кДж/кг∙К; Сv = 0,70 кДж/кг∙К). Рабочее тело рассматривать как идеальный газ (Pυ =RT). Цикл Дизеля в координатах Р-υ и T-s имеет следующий вид (рис. 3.1.8).
Ответ: lц = 528 кДж/кг; qI = 900 кДж/кг; qII = -372 кДж/кг; ηt = 59%; Задача 3.1.40. В паросиловой установке, работающей при начальных параметрах P1 = 5 МПа, t1 = 500°С и P2 = 0,01 МПа, введен вторичный перегрев пара при P1 = 3 МПа до начальной температуры t’ = t1 = 500°С. Определить термический КПД цикла с вторичным перегревом и повышение КПД установки за счет этого перегрева. Вторичный перегрев пара в паросиловой установке используется с целью избежать появления высокой степени влажности пара в конце процесса расширения. Высокая влажность пара приводит к гидравлическим ударам на лопатках турбины и вызывает коррозию этих лопаток. Одновременно вторичный перегрев пара приводит (при правильно выбранном промежуточном давлении перегрева) к некоторому повышению и КПД установки. Схема установки с вторичным перегревом пара показана на рис. 3.1.9, а ее цикл на рис. 3.1.10.
Рис. 3.1.9. Принципиальная схема паросиловой установки с вторичным перегревом пара
Рис. 3.1.10. Процессы расширения пара в паросиловой установке с вторичным перегревом пара
Пар из парового котла I (рис. 3.1.9) после прохождения пароперегревателя II поступает в турбину высокого давления III, где расширяется до промежуточного давления P1, а после турбины идет вновь к пароперегревателю II, где его температура при давлении Р' вновь доводится до первоначальной t1. С этой температурой t1 и давлением P1 пар поступает в турбину низкого давления IV, где уже расширяется до конечного давления P2. Затем пар проходит через конденсатор V и питательным насосом VI вода подается в паровой котел I. Цикл замыкается. Цикл паросиловой установки в диаграмме Т-s показан на рис. 3.1.10. Ответ: ηt = 33,6 %.
Истечение газов и паров Теоретические основы Истечение – процесс быстрых изменений состояния вещества во всех точках сечения потока вдоль оси потока. Решение задач на истечение газов через любые отверcтия обычно сводится к определению скорости его истечения и расхода. Процесс истечения рассматривается как адиабатический. Решение подобных задач начинается с определения соотношения давлений истечения Р2/Р1 где Р2 - наружное давление, куда происходит истечение газа, P1 - давление среды у входа в отверстие истечения. Найденное соотношение давлений истечения Р2/Р1 сравнивают с так называемым критическим соотношением давления (Р2/Р1)кр, которое для обычных (двухатомных) газов равно (при k = 1):
при k = 1,3 (для многоатомных газов) (Р2/Р1)кр = 0,546. Если адиабатическое истечение происходит при (Р2/Р1) > (Р2/Р1)кр, то режим истечения докритический и теоретическая скорость истечения газа определяется уравнением
где k - показатель адиабаты, υ1 - удельный объем газа у входа в отверстие истечения, w1,2 - потенциальная работа расширения. Для идеальных газов Р1υ1= RT1, уравнение 3.1.41 принимает вид
Теоретическая скорость истечения может быть найдена также по формуле
где i1 и i2—соответственно энтальпия газа в начальном и конечном состоянии, Дж/кг. Если энтальпию выразить в кДж/кг, то формула (3.1.43) принимает вид
Расход газа в этом случае определяется уравнением
где F - выходное сечение отверстия, м2. Если адиабатическое истечение газа происходит при (Р2/Р1) <= (Р2/Р1)кр, то режим истечения – критический и теоретическая скорость истечения определяется по уравнению
При k = 1,4 (для двухатомных газов) уравнение (3.1.46) принимает вид
При k = 1,3 (для многоатомных газов) уравнение (3.1.46) принимает вид
Критическая скорость истечения может быть определена и по уравнению
где iкр - энтальпия при критическом давлении Pкр. В формуле (3.1.49) энтальпия выражена в кДж/кг. Расход газа в этом случае будет максимальным:
При k = 1,4 уравнение (3.1.50) принимает вид
Здесь давление надо представлять в Па, а объем в м3/кг; расход получается в кг/с. Минимальное сечение сопла (отверстия) определяется уравнением
Примеры решения задач
Пример 3.1.16. Пропан из резервуара с постоянным давлением P1 = 10 МПа и температурой t1 = + 15°С вытекает в атмосферу через отверстие диаметром d = 10 мм. Определить скорость истечения пропана и его секундный расход. Наружное давление равно Р2 = 0,1 МПа. Процесс расширения считать адиабатическим, k =1,3. Решение Определяем отношение Р2/Р1. Оно равно 0,1/10 = 0,01. Следовательно, оно меньше критического отношения давлений, составляющего 0,546. Поэтому скорость истечения будет равна критической, и будет определяться формулой (3.1.48):
Секундный расход газа равен (по формуле (5) при k = 1,3)
где
Следовательно,
Задачи для самостоятельного решения
Задача 3.1.41. В одном из соединений трубопровода образовалась неплотность, эквивалентная отверстию F = 1 мм2. Давление газа в трубопроводе P1 = 7,0 МПа, температура газа в трубопроводе (t1 = 45°С, молекулярная масса газа μ = 20). Показатель адиабатического процесса истечения принимается равным 1,3. Определить суточную потерю газа, принимая его подчиняющимся уравнению Клапейрона Pυ = RT. Наружное давление Р2=0,1 МПа. Ответ: Gсут = 1106 кг/сут. Задача 3.1.42. Определить конечную температуру t2, удельную потенциальную работу w1,2, линейную скорость С2 и массовую скорость u2 при адиабатическом истечении водяного пара как идеального газа от начального состояния P1 = 1,0 МПа и t1 = 400°Сдо конечного давления Р2 = 0,8 МПа. Средняя молярная теплоемкость СРт = 36,07 кДж/кмоль∙К. Ответ: t2 = 366 оС; w1,2 = 67,7 кДж/кг; С2 = 368,3 м/с; u2 = 1003,5 кг/м2. Теория теплообмена Теплопроводность Теоретические основы В основе процесса передачи тепла теплопроводностью лежит закон Ж.Фурье (1822) утверждающий, что количество тепла δQ передаваемое через элементарную поверхность dF, за элементарный промежуток времени dτ пропорционально температурному градиенту
где λ – коэффициент пропорциональности, называемый коэффициентом теплопроводности и определяющий количество тепла, которое проходит в единицу времени через единицу поверхности на единицу длины при разности температур в один градус, [Вт/м∙К] – справочная величина, берется по соответствующим таблицам. Коэффициент теплопроводности определяет способность тела проводить тепло путем непосредственного контакта между его элементами. Знак минус в уравнении (3.2.1) отражает противоположность направлений векторов теплового потока и температурного градиента, т.е. по направлению теплового потока идет снижение температуры по мере увеличения толщины стенки. Количество тепла, передаваемого через единицу площади в единицу времени называется плотностью теплового потока, q
В интегральной форме уравнения (3.2.1) и (3.2.2) для плоской стенки имеют вид
Это значит, что количество тепла, передаваемого теплопроводностью (3.2.4) прямо пропорционально коэффициенту λ и разности температур на границах этой стенки (t1 – t2) и обратно пропорционально толщине стенки δ. В условиях плоской многослойной стенки уравнение для определения теплового потока принимает вид:
где t1 – t2 - разность граничных температур на входе в первую стенку и на выходе последней. Температура на поверхности слоев в многослойной стенке определяется уравнениями:
Для однослойной цилиндрической стенки тепловой поток равен (на единицу длины трубы)
Для многослойной цилиндрической стенки плотность теплового потока, отнесенная на единицу длины равна
где d1, d2…dn – соответственно внутренний и последующие к наружному диаметры трубы, м. Температура на поверхности слоев многослойной цилиндрической стенки:
и т.д.
Примеры решения задач
Пример 3.2.1. Определить тепловой поток через поверхность 1 м газопровода с внутренним диаметром 1000 мм и толщиной стенки δ1=10 мм, изолированного двумя слоями изоляции с толщиной соответственно δ2=10мм и δ3=7 мм. Коэффициенты теплопроводности трубы в изоляции соответственно равны λ1=65 Вт/м∙К, λ2=0,035 Вт/м∙К и λ3=0,23 Вт/м∙К. Температура на внутренней поверхности газопровода t1=55оС, а на наружной поверхности изоляции t4=+2оС. Решение 1. Для многослойной цилиндрической стенки плотность теплового потока на единицу длины газопровода определяется уравнением (3.2.7а)
2. Если изоляционные слои поменять местами, то тепловой поток на единицу длины в этом газопроводе составит (при тех же граничных температурах):
т.е. тепловой поток от замены последовательностей слоев изоляции увеличится на
Это значит, что на величину теплового потока влияет не только теплопроводность изоляции, ее толщина, но и последовательность расположения слоев изоляции. Вывод этот справедлив естественно только для криволинейных стенок, в частности, цилиндрических. Пример 3.2.2. Определить температуру на границах слоев трехслойной изоляции газопровода. Наружный диаметр трубы 1420 мм, а толщина стенки трубы 10 мм, а слоев изоляции соответственно δ1=8 мм,
δ2=12 мм и δ3=25 мм. Коэффициенты теплопроводности трубы и изоляционных материалов λтр=55 Вт/м∙К, λ1=0,035 Вт/м∙К, λ2=0,06 Вт/м∙К и λ3=0,12 Вт/м∙К. Температура на внутренней поверхности трубы t1=60оС, а на наружной поверхности изоляции tн.п.=+5оС. Решение 1. Согласно уравнению (3.2.7а) тепловой поток на единицу длины трубопровода составит
2. Температура на наружной поверхности трубы определяется уравнением (3.2.8)
т.е. температура наружной стенки трубы практически совпадает с температурой на внутренней поверхности, т.к. металл хорошо проводит тепло. 3. Температура между первым и вторым изоляционным слоем по уравнению (3.2.8а) равна
4. Температура между вторым и третьим слоем изоляции по уравнению (3.2.8а) составит
5. На поверхности изолированной трубы температура задана величиной tн.п.=+5оС. Эта температура позволяет определить температуру t’4 и со стороны наружной изоляции по уравнению
Задачи для самостоятельного решения
Задача 3.2.1. Определить удельный и полный тепловой поток через бетонную стенку компрессорного цеха толщиной 250 мм, если температуры на внутренней и наружной поверхности соответственно равны t1=+15oC и t2=-25oC. Коэффициент теплопроводности бетонной стенки λб=1,55 Вт/м∙К. Общая поверхность компрессорного цеха F=600 м2. Ответ: q=248 Вт/м2; Q=148,8 кВт=0,8598 ккал/час. Задача 3.2.2. Определить коэффициент теплопроводности плоской кирпичной стенки печи толщиной 240 мм, если температура на внутренней поверхности стенки составляет t1=450оС, а на наружной поверхности t2=45oC. Потери тепла через стенку составляют q=360 Вт/м2. Ответ: λ=0,21 Вт/м∙К. Задача 3.2.3. Слой льда над поверхностью воды имеет толщину δл=200 мм. Температуры на нижней и верхней поверхности льда соответственно равны t1=0оС, t2=-20oC. Определить удельный тепловой поток через поверхность льда, если теплопроводность льда λл=1,55 Вт/м∙К. Как изменится тепловой поток, если лед покроется снегом толщиной 160 мм с коэффициентом теплопроводности λс=0,50 Вт/м∙К, а температура на поверхности снега будет равна t2с=-10oC? Ответ: 1) qл=230 Вт/м2; 2) тепловой поток уменьшится в 9 раз. Задача 3.2.4. Трубу внешним диаметром 30 мм покрывают тепловой изоляцией с коэффициентом теплопроводности λ=0,1 Вт/м∙К. Коэффициент теплоотдачи во внешнюю среду составляет α2=5 Вт/м2∙К. Целесообразно ли в данном случае использовать такую изоляцию? Ответ: нет. Задача 3.2.5.Обмуровка печи состоит из слоев шамотного (δ1=120 мм) и красного (δ3=250 мм) кирпичей, между которыми диатомитовая засыпка (δ2=50 мм). Коэффициенты теплопроводности λ1=0,93 Вт/м∙К; λ2=0,14 Вт/м∙К; λ3=0,70 Вт/м∙К. Какой толщины будет слой из красного кирпича, если отказаться от диатомитовой засыпки, чтобы тепловой поток через обмуровку остался неизменным? Ответ: 500 мм. Задача 3.2.6. Плоская стенка бака площадью 5 м2 покрыта двухслойной тепловой изоляцией. Стенка бака стальная толщиной δ1=8 мм; λ1=46,5 Вт/м∙К. Первый слой выполнен из новоасбозурита толщиной δ2=50 мм; λ2=0,179 Вт/м∙К. Второй слой изоляции – известковая штукатурка толщиной δ3=10 мм; λ3=0,698 Вт/м∙К. Температура внутренней поверхности стенки бака 250 оС, внешней поверхности изоляции 50 оС. Вычислить количество тепла, передаваемого через стенку, температуры на границах слоев изоляции. Ответ: 680,8 Вт/м2; 249,9 оС; 59,7 оС.
Конвективный теплообмен
Теоретические основы
Обычно тепловой поток при конвективном теплообмене определяют по закону Ньютона:
где, a-коэффициент теплоотдачи, Вт/м2·К; tж, tc- температура жидкости и стенки, около которой движется эта жидкость, 0С; F- поверхность передачи тепла, м2. Величину a определяют из критериальных уравнений полученных на основе теории подобия или теории размерностей. В частности для свободной конвекции можно пользоваться уравнением:
где Nu- критерий Нуссельта
где l - определяющий геометрический размер (для трубы – диаметр, для пластины – длина и т.п.); Gr - коэффициент Грасгофа – критерий опредялющий действие свободной конвенции; λж – коэффициент теплопроводности, Вт/м·К.
где gп - ускорение свободного падения, qп=9,81 м/с2; b - термический коэффициент объемного расширения для газов
Dt - температурный перепад между средой и поверхностью теплообмена;nж- кинематическая вязкость; Pr-критерий Прандтля
где a- коэффициент температуропроводности; ρ – плотность, кг/м3;
Значения С и m уравнения 3.2.11 приведены в табл. 3.2.1. В условиях вынужденной конвекции, т.е когда теплоноситель движется за счет внешних сил критериальное уравнение для определения коэффициента теплоотдачи имеет вид:
При ламинарном движении жидкостей в трубах критериальное уравнение дополняется множителем Grж0,1, где Re – критерий Рейнольдса
ω – линейная скорость жидкостей в трубе, м/с. Значения коэффициентов С, n и m уравнения 3.2.17 приведены в табл. 3.2.2. Таблица 3.2.1 Численные значения коэффициентов С и m для различных условий теплообмена при свободной конвекции
Таблица 3.2.2 Численные значения коэффициентов C, n, m для различных условий теплообмена при вынужденной конвекции
Примеры решения задач
Пример 3.2.3. Температура поверхностей стены компрессорного цеха высотой 4 м равна tс=10 0С температура воздуха в цехе составляет tв=25 0С. Определить коэффициент теплоотдачи от воздуха к стене цеха. Решение Теплообмен здесь осуществляется за счет свободной конвекции, следовательно, необходимо воспользоваться уравнением 3.2.11. Критерии
В данном случае определяющим размером у критерия Gr будет высота цеха l=4 м,
Кинематическая вязкость воздуха при температуре tв=25 оС составит ν=15,53∙10-6 м2/с. Следовательно,
Физические параметры воздуха при температуре tв=25 оС, составляют: плотность ρ=1,185 кг/м3; теплоёмкость Ср=1,005 кДж/кг∙К=1005 Дж/кг∙К; кинематическая вязкость ν=15,53∙10-6 м2/с; коэффициент теплопроводности λ=2,634∙10-2 вт/м∙К. Следовательно, критерий Прандтля равен:
Произведение критериев Gr и Pr составляет
Согласно данным табл. 3.2.1 режим движения воздуха здесь будет турбулентным, следовательно, коэффициенты уравнения 3.2.11 будут в данном случае равны С=0,15, т=0,33. Критерий Нуссельта:
Отсюда по уравнению 3.2.12 коэффициент теплоотдачи
По уравнению 3.2.10 плотность теплового потока равна
Пример 3.2.4. Определить коэффициент теплоотдачи от газа к внутренней поверхности газопровода диаметром d=1020 мм, если температура стенки трубы tc=40 0С, а температура газа в трубе tг=60 0С. Линейная скорость газа w=3 м/с. Газ - метан. Давление в трубопроводе 4 МПа. Решение При теплообмене в трубах определяющим критерием, характеризующим режим течения, является критерий Рейнольдса
Коэффициент кинематической вязкости входящий в критерий Рейеольдса связан с коэффициентом динамической вязкости уравнением
где ρ - плотность газа. Считая газ в первом приближении идеальным, подчиняющимся уравнению Клайперона (РV=RT) плотность метана (СН4) равна:
Коэффициент динамической вязкости при параметрах Р=4 МПа и t=60 0С составляет Z=12,57∙10-6 Н∙с/м2=12,57∙10-6 кг/м∙с. Следовательно, кинематическая вязкость
Следовательно, критерий Рейнольдса в данном случае будет равен
Так как режим движения явно турбулентный, то расчет теплообмена производится по формуле:
При температурах газа tг=60 0С и стенки трубы tс=40 0С численные значения физических величин ν, ρ, Ср, λ, входящих в критерий Прандтля, равны при температуре tг=60 0С: ν=0,542∙10-6 м2/с; ρ=23,2 кг/м3; Ср=2,507 кДж/кг∙К; l=86,7∙10-3Вт/м∙К. При температуре tc=40 0C: ν=0,487∙10-6 м2/с; ρ=24,64 кг/м3; Ср=2,507 кДж/кг∙К; l=86,7∙10-3 Вт/м∙К. Следовательно, при температуре газа tг=60 0С, критерий Прандтля равен:
При температуре tс=40 0C, критерий Прандтля равен:
Численные значения критерия Прандтля совпадают, следовательно, определение критерия Nu можно вести по уравнению:
Так как
Следовательно, за единицу длины l=1 м от газа к стенке передается следующее количество тепла: Ql=a∙f(tг-tс)=138,72∙pd(tг-tс)= 288,04∙3,14∙1,02(60-40)=18450,9 кВт.
Задачи для самостоятельного решения
Задача 3.2.7. Природный газ после сжатия на КС проходит по трубам аппаратов воздушного охлаждения, где охлаждается потоком наружного воздуха. Температура воздуха 200С. Скорость w=5м/с. Расположение труб в АВО коридорное, диаметр трубы 25 мм. Определить коэффициент теплоотдачи при поперечном омывании воздухом труб АВО. Ответ: a=74,8 Вт/м2∙К Задача 3.2.8. Отопление цеха компрессорной станции производится горизонтальным трубопроводом с наружным диаметром 25 мм, обогреваемым конденсирующим паром. Средняя температура наружной поверхности трубопровода 95 0С, температура в помещении должна быть 20 0С. Определить необходимую длину трубопровода, если расчетная мощность отопительной системы составляет 25 кВт=25000 Вт. Ответ: L=69,9 м. Задача 3.2.9. Воздух течет внутри трубы, имея среднюю температуру tв=150 оС, давление Р1=1 МПа, скорость ω=6 м/с. Определить тепловой поток, отнесенный к 1 м длины трубы, если внутренний диаметр d1=70 мм, толщина ее δ1=3 мм, коэффициент теплопроводности λст=20 Вт/м∙К. Снаружи труба омывается горячими газами. Температура и коэффициент теплоотдачи горячих газов, соответственно tг=600 оС; α2=40 Вт/м2∙К. Ответ: 1334 Вт/м. Задача 3.2.10. Определить средний коэффициент теплоотдачи при течении трансформаторного масла в трубе диаметром 8 мм и длиной 1 м, если средняя по длине трубы температура масла tж=80 оС, средняя температура стенки трубы tс=20 оС, скорость масла ω=0,6 м/с. Ответ: 139,6 Вт/м2∙К. Теплообмен излучением Теоретические основы Энергия, излучаемая с поверхности тела, имеющего температуру Т, определяется уравнением:
где ε-степень черноты тела; С0-коэффициент излучения абсолютно черного тела; С0=5,67Вт/м2∙К4. Теплообмен излучением между двумя параллельными поверхностями определяется уравнением: где εпр-приведенная степень черноты двух тел:
ε1 и ε2 – степени черноты первого и второго тела; Т1 и Т2 – абсолютная температура тела; F- поверхность тел, м2. Теплообмен излучением, когда одно тело расположено в другом (т.е. тело в оболочке) рассчитывается по уравнению (3.2.20), но приведенная степень черноты определяется уравнением:
если F1‹‹F2, то εпр= ε. Теплообмен излучением между излучающим газом и определяющим его объем оболочкой определяется уравнением:
где εоб – степень черноты оболочки; εг – степень черноты газа. Степень черноты газа обычно определяется по номограммам с учетом парциального давления компонентов газа и длины пути луча, определяемого по формуле: L=3,6∙V/F (3.2.24) где V – объем газа м3; F – площадь оболочки газа, м2.
Примеры решения задач
Пример 3.2.5. Продукты сгорания газотурбинной установки выбрасываются в атмосферу через дымовую трубу диаметром 2 м при атмосферном давлении. Дымовые газы содержат 20 % СО2 и 6,5 % Н2О. Парциальное давление СО2 = 0,016 МПа, а Н2О = 0,0075 МПа. Средняя температура газов в выхлопной трубе 450 0С, а температура трубы 120 0С. Степень черноты поверхности трубы 0,92. Какое количество тепла излучением передается от газов к стенкам трубы на 1 м ее длины при атмосферном давлении в газоходе. Решение 1. Средняя длина пути на 1 м длины трубы-газохода определяется уравнением
где V – объем газа на 1 м длины выхлопной трубы; π – параметр трубы (по поверхности оболочки газа). 2. Так как степень черноты газа определяется по номограммам, где по оси абсцисс отложена температура газов, а параметром является произведение парциального давления на длину луча, то РСО2 ∙l=0,016∙7,2=0,1152 МПа∙м; РН2О∙l=0,0075∙7,2=0,054 МПа∙м. По номограммам находим степень черноты газа: eСО2=0,195; eН2О=0,3. Степень черноты дымовых газов: eг=eCO2+eH2O=0,495. 3. Используя соотношение 3.2.23, найдем количество тепла передаваемого излучением на единицу длины трубы:
где поверхность воспринимающая тепло излучением на 1 м длины равна F=pd=3,14∙2=6,28 м2. Задачи для самостоятельного решения
Задача 3.2.11. В камере сгорания газотурбинной установки сжигается топливо в количестве G=12000 кг/час. Температура горения топлива 1700 0С. Степень черноты газов 0,45. Степень черноты жаровой трубы 0,95. Определить температуру стенок жаровой трубы камеры сгорания, если ее размеры: диаметр d=1,2 м; длина l= 2 м. Низшая теплота сгорания топлива Q=46000 кДж/кг; КПД камеры сгорания η=0,97. Ответ: Т2=1193,8 0С. Задача 3.2.12. Определить теплоту излучения 1 м неизолированного отопительного трубопровода диаметром 25 мм в компрессорном цехе, если температура его наружной поверхности равна 85 оС, а температура в помещении 20 оС. Степень черноты поверхностей трубы ε=0,85. Определить, какую долю составляет тепловой поток излучением от общей теплоотдачи отопительного трубопровода, если общий тепловой поток составляет 4500 Вт/м2. Ответ: 34,3 Вт/м2; 7,6 %. Задача 3.2.13. Определить удельный лучистый тепловой поток q между двумя параллельно расположенными плоскими стенками, имеющими температуры t1=200 оС и t2=30 оС и степень черноты ε1=0,6, ε2=0,7, если между ними нет экрана. Определить тепловой поток при наличии экрана со степенью черноты εЭ=0,05 (с обеих сторон). Ответ: 1126 Вт/м2; 57 Вт/м2. Задача 3.2.14. Определить потери теплоты в единицу времени с 1 м длины горизонтально расположенной цилиндрической трубы, охлаждаемой свободным потоком воздуха, если температура стенки трубы tс=150 оС, температуры воздуха в помещении tв=15 оС, диаметр трубы d=210 мм. Степень черноты трубы εс=0,9. Ответ: 1515 Вт/м.
Теплопередача
Теоретические основы
Теплопередачей принято называть теплообмен между двумя жидкими или газообразными средами, разделенными твердой перегородкой. Количество тепла, передаваемого от одного теплоносителя к другому через разделяющую их стенку в единицу времени, определяется уравнением: Q=KF(t1-t2), Вт (3.2.25) где К – коэффициент теплопередачи характеризующий количество тепла передаваемого в единицу времени через единицу поверхности при разности температур в один градус, Вт/м2∙К; t1 и t2 - температуры теплоносителей. При теплопередаче через плоскую однородную стенку коэффициент теплопередачи К определяется уравнением:
где a1 и a2 коэффициенты теплоотдачи на поверхностях стенки со стороны нагревающего теплоносителя a1 и нагреваемого a2; l-коэффициент теплопроводности материала стенки (справочная величина); δ-толщина стенки. Для многослойной плоской стенки коэффициент теплопередачи К равен:
где δi,, li - толщина и коэффициент теплопроводности слоев стенки. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
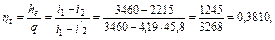
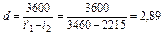 кг/кВт∙ч.
кг/кВт∙ч. кг/ч.
кг/ч.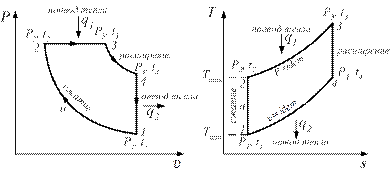
 = 83%.
= 83%.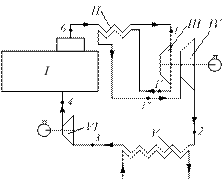

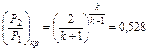 , (3.1.40)
, (3.1.40) м/с (3.1.41)
м/с (3.1.41) м/с (3.1.42)
м/с (3.1.42)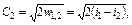 м/с (3.1.43)
м/с (3.1.43)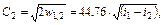 м/с. (3.1.44)
м/с. (3.1.44)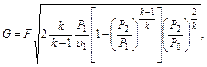 (3.1.45)
(3.1.45)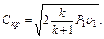 (3.1.46)
(3.1.46)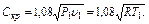 (3.1.47)
(3.1.47)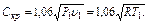 (3.1.48)
(3.1.48)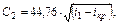 (3.1.49)
(3.1.49)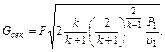 (3.1.50)
(3.1.50)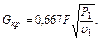 (3.1.51)
(3.1.51)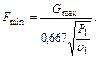 (3.1.52)
(3.1.52) м/с.
м/с.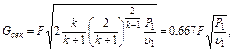
 м2,
м2, м3/кг,
м3/кг,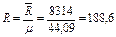 кДж/кг∙К.
кДж/кг∙К. кг/с.
кг/с.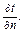
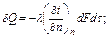 (3.2.1)
(3.2.1) Вт/м2 (3.2.2)
Вт/м2 (3.2.2)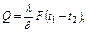 Вт (3.2.3)
Вт (3.2.3) Вт/м2 (3.2.4)
Вт/м2 (3.2.4) Вт/м2 (3.2.5)
Вт/м2 (3.2.5)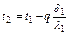 (3.2.6)
(3.2.6)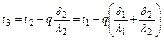 (3.2.6а)
(3.2.6а)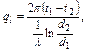 Вт/м2 (3.2.7)
Вт/м2 (3.2.7)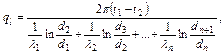 Вт/м2 (3.2.7а)
Вт/м2 (3.2.7а)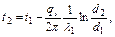 оС (3.2.8)
оС (3.2.8) (3.2.8а)
(3.2.8а)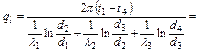
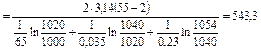 Вт/м2.
Вт/м2.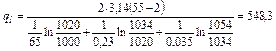 Вт/м2,
Вт/м2, .
.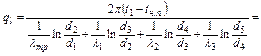
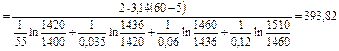 Вт/м2.
Вт/м2. оС.
оС.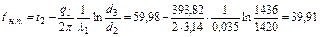 оС.
оС.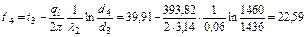 оС.
оС.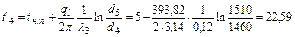 оС.
оС. (3.2.9)
(3.2.9) (3.2.10)
(3.2.10)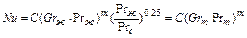 (3.2.11)
(3.2.11)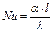 , (3.2.12)
, (3.2.12)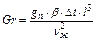 , (3.2.13)
, (3.2.13)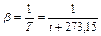 , (3.2.14)
, (3.2.14) , (3.2.15)
, (3.2.15)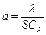 , (3.2.16)
, (3.2.16)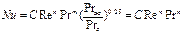 (3.2.17)
(3.2.17)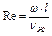 , (3.2.18)
, (3.2.18) и Pr определяется уравнениями 3.2.13 и 3.2.15.
и Pr определяется уравнениями 3.2.13 и 3.2.15.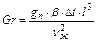 .
.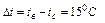
 К-1.
К-1.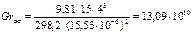
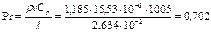
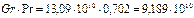
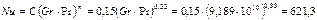
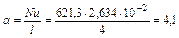 Вт/м2∙К.
Вт/м2∙К.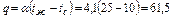 Вт/м2.
Вт/м2.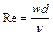
 , м2/с,
, м2/с,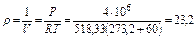 кг/м3,
кг/м3,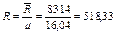 Дж/кг∙К.
Дж/кг∙К.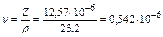 м2/сек.
м2/сек. .
. .
.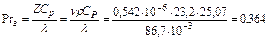 .
.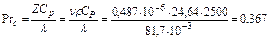 .
.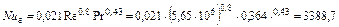 ,
,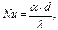 то при l=86,7∙10-3 Вт/м∙К.
то при l=86,7∙10-3 Вт/м∙К.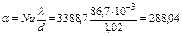 кВт/м2∙К.
кВт/м2∙К.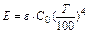 (3.2.19)
(3.2.19)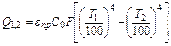 (3.2.20)
(3.2.20) (3.2.21)
(3.2.21)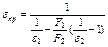 (3.2.22)
(3.2.22)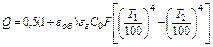 (3.2.23)
(3.2.23)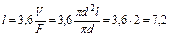 м,
м,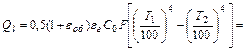
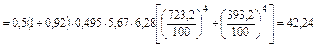 кВт/м.
кВт/м. , (3.2.26)
, (3.2.26) , (3.2.27)
, (3.2.27)