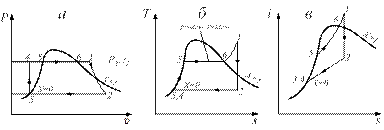|
|
Процессы изменения состояния веществаТеоретические основы Термодинамическим процессом называется любое изменение состояния вещества, например, газа. Вид процесса обычно определяется тем, что задано условие постоянства какой-либо функции состояния (например, и = idem, i = idem, s = idem и т. п.) или какого-либо параметра (например, P =idem, t=idem, υ=idem). В ряде случаев процесс может быть задан условием о равенстве нулю какого-либо эффекта в процессе (например, равенство нулю теплообмена, δq=0 ). Большинство процессов описывается общим уравнением политропы с постоянным показателем
Соотношения между парамет зависимости термодинами
Таблица 3.1.3. рами состояния, расчетные и проверочные ческих величин в процессах
или
где n - показатель политропы, являющийся постоянной величиной для данного процесса, который может в зависимости от вида процесса иметь численные значения от - ∞ до 0 и от 0 до + ∞. С и С1 - постоянные, характеризующие прохождение процесса через какую-либо точку процесса, например, точку 1, 2 . . .n.
Из уравнения (3.1.29) и (3.1.30) следуют различные простейшие процессы: Р=idem (изобарический) при n = 0 из уравнения (3.1.29); υ=idem (изохорический) при n=±∞ из уравнения (3.1.30); Рυ=idem (изопотенциальный, а для идеальных газов Рυ=RT, изотермический, t=idem) при n=1 из уравнений (3.1.29) либо (3.1.30) и т.п. Следовательно, политропический процесс это любой процесс и он становится определенным только после того, как задано значение показателя п. Решение задач на процессы обычно сводится к нахождению численных значений Р, υ, t в характерных точках, процесса (1,2), определению эффекта процесса (величины работы, подведенного или отведенного тепла и т. п.). Основные соотношения между параметрами состояния, расчетные и проверочные зависимости термодинамических величин в процессах указаны в табл. 3.1.3.
Примеры решения задач
Пример 3.1.11. 1 кг метана при постоянной температуре t1=+15°С и начальном давлении P1=3,5 МПа сжимается до давления P2=5,5 МПа. Определить удельный конечный объем и количество тепла, отводимого в процессе сжатия, затрачиваемую работу. Решение 1. Процесс изотермический, то есть по условию задачи температура газа в процессе сжатия остается неизменной t = + 15°С = idem. 2. Удельный начальный объем газа определяют из уравнения состояния
где R — газовая постоянная метана
Так как в изотермическом процессе, когда n = 1
то конечный объем газа равен
3. Работа, затрачиваемая на сжатие 1 кг метана, определяется из уравнения
4. Количество тепла, отводимого от газа, численно равно работе, затраченной на сжатие. Следовательно q = - 67,527 кДж/кг. Пример 3.1.12. Метан массой 1 кг адиабатически расширяется с давления Р1=5,5 МПа и температуры 50°С до давления Р2=1 МПа. Найти конечные объем, температуру, потенциальную и термодинамическую работу, изменение внутренней энергии и энтальпии. Показатель процесса расширения принять равным k = 1,4. Решение 1.Начальный удельный объем находится из уравнения Клапейрона. Газовая постоянная для метана 518,3 Дж/кг∙К.
2. Для адиабатического процесса справедливы уравнения вида
Отсюда
t2=T2-273,2≈75 oC. 3. Конечный объем в процессе расширения равен
4. Определение удельных значений работ осуществляется с помощью следующих уравнений Термодинамическая работа
Потенциальная работа
5. Изменение внутренней энергии и энтальпии в обратимом адиабатическом процессе соответственно равно термодинамической и потенциальной работам.
Задачи для самостоятельного решения Задача 3.1.29.В компрессоре сжимается воздух (молекулярная масса μ = 28,96) от начального состояния Р1 = 0,102 МПа и t1 = + 15°С до P2 = 0,408 МПа и t2=184,3°С. Теплоемкость воздуха принимается равной Cp = 1 кДж/кг°С. Определить удельную потенциальную работу сжатия w1,2, изменение энтальпии и полный теплообмен по балансу рабочего тела (q1,2= q*1,2+ q**1,2). Ответ: w1,2=-145,8 кДж/кг; i2 – i1=169,3 кДж/кг; q1,2=23,5 кДж/кг. Задача 3.1.30.Воздух в количестве 3 м3 расширяется политропно от Р1= 0,54 МПа и t1=45 0С до P2= 0,54 МПа. Объем, занимаемый при этом воздухом, становится равным 10 м3. Найти показатель политропы, конечную температуру, полученную работу и количество подведенной теплоты. Ответ: n = 1,06; t2= 21,4 0С;L = 1875 кДж; Q = 1575 кДж. Задача 3.1.31. В процессе политропного сжатия затрачивается работа, равная 195 кДж, причем в одном случае от газа отводится 250 кДж, а в другом – газу сообщается 42 кДж. Определить показатели общих политроп. Ответ: n = 0,9; n = 1,49. Пары Теоретические основы Различают следующие понятия паров разного рода жидкостей: воды, фреонов, углекислоты. 1. Влажный насыщенный пар - это смесь жидкости и сухого пара, то есть в такой смеси частицы жидкости равномерно распределены в паре. Состояние влажного насыщенного пара характеризуется параметрами Р и υ, Р и х, t и х. Параметры Р — t не определяют состояния влажного насыщенного пара, так как в этой области изобара (Р = idem) и изотерма (t = idem) совпадают. Параметр х характеризует так называемую сухость пара, то есть отношение количества пара G” к количеству смеси в целом G = G’ + G”
При рассмотрении паров индексом ' обозначают все, что относится к воде (в данном случае G' — это количество воды в смеси), индексом “ обозначают все то, что относится к пару (в данном случае G” — это количество пара в смеси). Величину у = 1 - х называют влажностью пара
Величина х изменяется в диапазоне от 0 до 1
Если х = 0, то это вода (G = G’), пара в этом состоянии нет (G” = 0), если x = 1, то это сухой насыщенный пар, то есть пар полностью освобожден от примесей воды (G’ = 0, G = G”). Тепло, расходуемое на превращение 1 кг воды, предварительно нагретой до температуры кипения или, как ее иногда называют, до температуры насыщения (ts), в пар той же температуры (ts) и того же давления, называют скрытой теплотой парообразования или просто теплотой парообразования и обозначают буквой r. После того как жидкость полностью переведена в пар, и мы имеем сухой насыщенный пар, дальнейший подвод тепла вызывает повышение температуры пара и он становится перегретым паром. Таким образом, перегретым паром называется пар, температура которого выше температуры сухого насыщённого пара (t>ts) при том же давлении. Решение задач на пары обычно осуществляется с помощью i-s диаграммы или таблиц, характеризующих состояние насыщенного пара в зависимости от давления или от температуры на кривой насыщения.
Примеры решения задач
Пример 3.1.13.Определить состояние пара при следующих параметрах: 1) Р=0,5 МПа и υ=0,30 м3/кг, 2) P=1,0 МПа и t=200° С, 3) Р =2,0 МПа и t=212,4°С. Решение 1. Из данных табл. 3.1.4 видно, что давлению Р = 0,5 МПа соответствует удельный объем насыщенного пара υ’’ = 0,3749 м3/кг. Это же можно видеть и на i-s диаграмме, на линии х = 1. Величина υ’’ = 0,3749 м3/кг больше данного по условию задачи объема υ = 0,30 м3/кг. Это значит, что пар с объемом υ = 0,30 м3/кг является влажным насыщенным паром, а степень его сухости можно найти из соотношения объемов
Влажность пара y = 1- x = 1 – 0,78 = 0,22. 2. Из данных табл. 3.1.4 видно, что давлению Р = 1 МПа соответствует температура насыщения = 179,9 °С. Это видно и из диаграммы i-s на линии х = 1. Так как в данном случае пар имеет температуру 200 °С, то он перегрет, а температура перегрева tm = t - ts = 200 - 179,9 =20,1oC. 3. Давлению Р = 2,0 МПа соответствует температура насыщения ts = 212,4 °C. Следовательно, пар влажный насыщенный. Однако сказать, влажный он или сухой, то есть определить величину х и у нельзя, так как параметры Р и t здесь совпадают между собой и представляют в нижней части i-s диаграммы (где
Задачи для самостоятельного решения
Задача 3.1.32. Определить состояние водяного пара с давлением Р = 1 МПа, если его энтальпия i = 2680кДж/кг. Ответ: влажность пара y = 1 - x = 0,05. Задача 3.1.33. В резервуаре объемом 1,5 м3 содержится 5 кг воды и 8 кг сухого пара. Определить давление в резервуаре. Ответ: Задача 3.1.34. Определить массу и энтальпию 0,6 м3 пара влажностью у = 1-х = 0,2 при давлении Р = 0,3 МПа. Ответ: G=1,24 кг; I=2843,1 кДж. Задача 3.1.35.С помощью диаграммы i-s определить конечную температуру, термодинамическую и потенциальную работу процесса расширения, когда пар массой G = 10 кг расширяется от начальных параметров Р1 = 3,0 МПа и t1 = 350°С в изохорном процессе (υ=idem) до давления P2 = 2,0 МПа. Определить также количество отводимого тепла и конечную температуру. Ответ: t2=210 оС; Q1,2=-3,8 МДж. Задача 3.1.36. Пар массой G = 10 кг при степени сухости х = 0,90 и давлении Р = 1 МПа подогревается в процессе P=idem до температуры t2 = 300°С. С помощью диаграммы i-s определить начальные и конечные параметры пара, количество подведенного тепла, термодинамическую и потенциальную работу, изменение внутренней энергии. Ответ: Δи=0,39 МДж/кг; Q1,2=4,8 МДж; L1,2=900 кДж; W1,2=0. Задача 3.1.37. Пар с температурой 200°С расширяется изотермически (t=idem) от давления Р1 = 0,5 МПа до Р2 = 0,1 МПа. Определить количество тепла, сообщаемое пару, изменение внутренней энергии и работу расширения с помощью диаграммы i-s. Ответ: Δи=20 кДж/кг; количество тепла q1,2=373,8 кДж/кг; работа расширения q1,2=353,8 кДж/кг.
Таблица 3.1.4 Параметры сухого насыщенного пара и воды в зависимости от давления на кривой насыщения
Параметры критической точки: давление Рк=221,3 бар, температура tк=374,15° С, удельный объем υк= 0,00326 м3/кг, Таблица 3.1.5 Параметры сухого насыщенного пара и воды в зависимости от температуры на кривой насыщения
Параметры критической точки: температура tк=374,15°C, давление Рк=221,30 бар, удельный объем υк=0,00326 м3/кг, Задача 3.1.38. Перегретый пар по адиабате расширяется с давления Р1 = 0,5 МПа и температуры t1 = 250°С до давления P2 = 0,05 МПа. Определить с помощью i-s диаграммы параметры пара в начальной и конечной точках процесса, работу расширения, изменение внутренней энергии. Ответ: l1,2=Δи=370 кДж/кг; w1,2=Δi1,2=435 кДж/кг. Термодинамические циклы Циклом называется определенная последовательность процессов, образующих замкнутый контур, в котором рабочее тело возвращается в исходное состояние. Цикл называется термодинамическим, если в нем не учитываются потери, а массовый расход рабочего тела во всех стадиях цикла остается одним и тем же. Степень совершенства работы цикла характеризуется термическим КПД
где q2 –количество отводимого тепла в цикле Дж/кг; q1 –количество подведенного тепла в цикле Дж/кг. Внутренняя энергия, энтальпия, энтропия является функциями состояния, поэтому в круговых процессах изменение этих величин равно нулю.
Работа цикла
где
Примеры решения задач
Пример 3.1.14. Определить параметры состояния (Р, υ, t, u, i, s) в крайних точках цикла газотурбинной установки простейшей схемы, работающей при следующих исходных данных (рис. 3.1.3): начальное давление сжатия Р1 = 0,1 МПа,
конечное давление сжатия Р2 = 0,5 МПа, начальная температура сжатия t1 = + 15 °С, начальная температура процесса расширения t3 = 750 °С.
Рис. 3.1.3. Схема простейшей газотурбинной установки 1 – осевой компрессор; 2 – камера сгорания; 3 – турбина; 4 – нагрузка
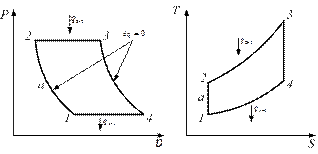
Рис. 3.1.4. Цикл газотурбинной установки в координатах Р-υ и Т-S
Внутреннюю энергию u, энтальпию i определить относительно Т0 = 0 К, а энтропию s определить относительно состояния при Т0 = 273,2 К, Р0=0,101 МПа. Для каждого процесса цикла определить работу, количество подведенного или отведенного тепла, изменение внутренней энергии, энтальпию и энтропию. Определить работу цикла, количество подведенного и отведенного тепла, термический КПД цикла, сравнить его с КПД цикла Карно, имеющего одинаковые с расчетным циклом максимальную и минимальную температуры. Построить цикл в координатах Р-υ и Т-S. Рабочее тело — 1 кг воздуха (R=0,287 кДж/кг∙К, СP=1,006 кДж/кг∙К; СV=СP – R=0,719 кДж/кг∙К). Для воздуха применимо уравнение состояния идеального газа Pυ = RT. Решение 1. Определение параметров состояния в крайних точках цикла. Точка 1. P1=0,1 МПа; t1=+ 15°С; Т1=t1 + 273,2=288,2 К;
i1=СP T1=1,006∙288,2 = 289,9 кДж/кг; ul = CV T1=0,719∙288,2 = 207,2 кДж/кг;
Следует заметить, что если определение энтропии в точке идет при совпадающем значении давления P1=Р0, то уравнение упрощается и принимает вид Точка 2.
t2=T2 - 273,2 = 183,5 °С;
i2=CP∙T2=1,006∙456,7=459,4 кДж/кг; и2=CV∙T2=0,719∙456,7=328,4 кДж/кг;
Точка 3. Р3=Р2=0,5 МПа; Т3=t3 + 273,2 = 1023,2 °К;
i3=CP∙T3=1,006∙1023,2=1029,3 кДж/кг; и3=CV∙T3=0,719∙1023,2=735,7 кДж/кг;
Точка 4. Р4=Р1=0,1 МПа;
t4=T4 - 273,2 = 376,6 °С;
i4=CP∙T4=1,006∙645,8=649,7 кДж/кг; и4=CV∙T4=0,719∙645,8=470,8 кДж/кг;
2. Построение цикла в координатах Р-υ и Т-s. Процессы, изображаемые в Р-υ и Т-s координатах, необходимо строить не менее чем по трем точкам. Для нахождения параметров промежуточных точек вначале надо принять произвольно значение одного какого-либо параметра таким образом, чтобы это значение находилось между его численными значениями в крайних точках процесса. Последующий параметр определяется из уравнения, характеризующего данный процесс, составленного для одной (любой) из крайних точек процесса и для промежуточной точки. Процесс 1-2. Точка «а». Принимаем Ра=0,3 МПа. По уравнению адиабаты идеального газа Pυk =C для точек «а» и 1 имеем Ра∙υkа = Р1∙υk1 или
ta=120,9 oC; ia=CP∙Ta=1,006∙394,1=396,5 кДж/кг; иa=CV∙Ta=0,719∙394,1=283,4 кДж/кг;
Аналогично определяются параметры на всех других процессах рассматриваемого цикла. По найденным значениям строится цикл в координатах Р-υ и Т-s. Масштаб выбирается произвольно исходя из численных значений параметров. 3. Определение работы, количества подведенного или отведенного тепла, изменение внутренней энергии, энтальпии и энтропии для каждого процесса цикла. Процесс 1-2 (адиабатический, δq = 0) q1,2 = Δu + l1,2 = Δi + w1,2 = 0 Потенциальная работа w1,2 = i1 – i2 = CP(T1 – T2) = 1,006(288,2 – 456,7) = - 169,5 кДж/кг – работа затрачивается. Термодинамическая работа l1,2 = u1 – u2 = CV(T1 – T2) =0,719(288,2 - 456,7) = - 121,2 кДж/кг; Δi = i2 – i1 = 169,5 кДж/кг; Δu = u2 – u1 = 121,2 кДж/кг, Δs1,2 = 0, так как q1,2 = 0. Процесс 2-3 (изобарический, Р = idem) l2,3 = P2(υ3 – υ2) = 0,5∙105(0,587 – 0,262) = 0,162∙105 кДж/кг; w2,3 = 0; q2,3 = i3 – i2 = CP(T3 – T2) = 1,006(1023,2 — 456,7) = 569 кДж/кг, - тепло подводится Δu2,3 = CV(T3 – T2) = 0,719(1023,2 - 456,7) = 407,3 кДж/кг; l2,3 = q2,3 + Δu2,3 = 569,7 - 407,3 = 162 кДж/кг,
Процесс 3-4 (адиабатический, δq = 0) q3,4 = Δu3,4 + l3,4 = Δi3,4 + w3,4 = 0; w3,4 = i3 – i4 = CP(T3 – T4) = 1,006(1023,2 – 645,8) = 379,7 кДж/кг; l3,4 = u3 – u4 = CV(T3 – T4) =271,4 кДж/кг; Δs3,4 = 0, так как q3,4 = 0. Процесс 4-1 (изобарический, Р = idem) w4,1 = 0; q4,1 = Δi4,1 + w4,1 = CP(T1 – T4) ==1,006(288,2 - 645,8)= - 359,7 кДж/кг – тепло отводится. Δu4,1 = CV(T1 – T4) = 0,719(288,2 - 645,8) = - 257,1 кДж/кг; l4,1 = P (υ1 – υ4) = 0,5∙105(0,827 - 1,85) = - 0,102∙105 кДж/кг; из первого начала термодинамики q4,1 =Δu4,1 + l4,1 имеем: l4,1 = q4,1 – Δu4,1 = - 359,7 - (-257,1) = - 102,6 кДж/кг – работа подводится
или
Данные вычислений сводятся в табл. 3.1.6, 3.1.7. Таблица 3.1.6 Результаты вычислений по точкам
Таблица 3.1.7 Результаты вычислений по процессам
Работа цикла Термодинамическая работа lц = l1,2 + l2,3 + l3,4 + l4,1 = - 121,2 + 162 + 271,4 - 102,6 ≈ 210 кДж/кг. Потенциальная работа wц = w1,2 + w2,3 + w3,4 + w4,1 = - 169,5 + 379,7 = 210 кДж/кг. В круговых процессах lц = wц. Количество полезно использованного тепла в цикле qпол = q2,3 – q4,1 = 210 кДж/кг. В круговом термодинамическом процессе количество подведенного тепла численно равно работе: q = lц = wц = 210 кДж/кг. Термический КПД цикла
КПД цикла Карно, имеющего одинаковые с расчетным циклом максимальную и минимальную температуры
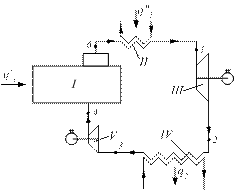
Пример 3.1.15. Провести термодинамический расчет цикла паросиловой установки (цикл Ренкина), работающей при следующих исходных данных. Начальное давление пара, то есть давление перед турбиной Р1 = 5 МПа = 50 Бар. Начальная температура пара, то есть температура пара перед турбиной t1 = 500 °С; T1 = t1 + 273,2 = 773,2 К. Конечное давление отработанного пара, т.е. давление пара за турбиной, в конденсаторе Р2 = 0,01 МПа = 0,1 бар. Требуется определить: 1) параметры пара в крайних точках цикла и представить цикл в координатах Р-υ и T-s и i-s; 2) внутренний абсолютный КПД цикла; 3) удельный часовой расход пара; 4) удельный часовой расход тепла; 5) количество охлаждающей воды, необходимой для конденсации пара в течение 1 часа, если вода нагревается при этом на 10°C. Мощность паросиловой установки принимается равной N = 2500 кВт. Решение Паросиловая установка по циклу Ренкина работает следующим образом (рис. 3.1.5). Вода насосом V подается в паровой котел I, при этом давление ее повышается с величины Р2 до Р1. Так как вода практически не сжимается (υ=const), то в координатах Р-υ (рис. 3.1.6) этому процессу соответствует процесс 3-4 (υ=idem), а в координатах Т-s и i-s этот процесс из-за малости масштаба практически выглядит как совмещенная точка 3-4 (Слишком близко друг от друга здесь расположены изобары P1 и Р2).
Рис. 3.1.5. Принципиальная схема паросиловой установки
В паровом котле вода подогревается вначале от температуры точки 4 до температуры точки 5, где она достигает величины температуры кипения. Эта температура будет больше или меньше в зависимости от давления P1. Так при давлении P1 = 0,1 МПа температура в точке 5 будет равна ≈ 100°С; а при Р = 0,2 МПа кипение, воды будет начинаться уже при температуре ≈ 120°С и т.д. Таким образом, отрезок изобары 4-5 в координатах Р-υ -соответствует процессу нагревания воды при постоянном давлении до температуры кипения. Температуру кипения, при которой вода превращается в пар, называют температурой насыщения, а пар, образующийся при этом, — влажным насыщенным паром.
Рис. 3.1.6. Цикл паросиловой установки в координатах Р-υ и T-s и i-s
При дальнейшем подводе тепла в паровом котле 1 количество жидкой фазы постепенно уменьшается, а количество пара увеличивается. Температура смеси остается постоянной (рис. 3.1.6), так как все подводимое тепло идет на испарение жидкой фазы. Этот процесс на рис. 3.1.6 изображается отрезком 5-6, который одновременно является изобарой и изотермой. То есть процесс парообразования 5-6 является изобарно-изотермическим. В точке 6 последняя капля воды превращается в пар и пар теперь называется сухим насыщенным паром. При дальнейшем подводе тепла в пароперегревателе II (q’’1) при том же давлении P1 происходит увеличение температуры пара, пар перегревается. Точка 1 на рис. 3.1.6 соответствует, состоянию перегретого пара и, в зависимости от температуры T1, может лежать дальше или ближе от точки 6. Далее пар с параметрами P1, T1, поступает в паровую турбину, где расширяется адиабатически до давления Р2. После расширения пара в паровой турбине и получения полезной работы от турбины отработанный пар поступает в холодильник-конденсатор IV, где за счет внешнего охлаждения полностью конденсируется. Вода вновь поступает на вход насоса V и цикл повторяется. Для цикла Ренкина характерно, прежде всего, то, что в нем не учитываются какие-либо потери в различных стадиях цикла, присутствует одно и то же количество вещества и, главное, происходит полная конденсация водяных паров в холодильнике-конденсаторе на линии 2-3. При этом отводится тепло в количестве q2. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|













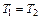

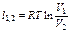



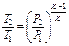


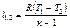



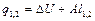


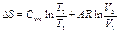
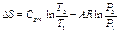
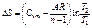

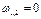
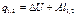


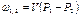


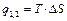 q1,2=Сvm(T2-T1)
q1,2=Сvm(T2-T1)





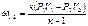

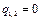

 (3.1.29).
(3.1.29). (3.1.30).
(3.1.30).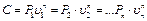 (3.1.31).
(3.1.31). (3.1.32).
(3.1.32). м3/кг,
м3/кг, Дж/(кг∙К).
Дж/(кг∙К). (3.1.33)
(3.1.33) м3/кг.
м3/кг.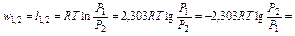
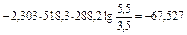 кДж/кг.
кДж/кг. м3/кг.
м3/кг. .
. К;
К; м3/кг.
м3/кг.
 кДж/кг.
кДж/кг. кДж/кг;
кДж/кг;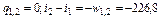 кДж/кг.
кДж/кг. . (3.1.34)
. (3.1.34) . (3.1.35)
. (3.1.35) (3.1.36)
(3.1.36) .
. ) одну линию.
) одну линию.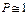 МПа.
МПа. , (3.1.37)
, (3.1.37)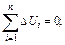

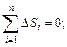 (3.1.38)
(3.1.38) (Дж/кг), (3.1.39)
(Дж/кг), (3.1.39)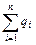 - суммарное количество тепла в процессах, составляющих цикл;
- суммарное количество тепла в процессах, составляющих цикл;  - суммарная термодинамическая работа;
- суммарная термодинамическая работа; 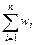 - суммарная потенциальная работа.
- суммарная потенциальная работа.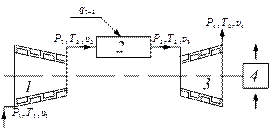
 м3/кг;
м3/кг; кг/м3;
кг/м3; кДж/кг∙К.
кДж/кг∙К.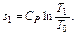
 К;
К;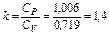 ;
; м3/кг;
м3/кг;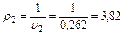 кг/м3;
кг/м3; кДж/кг∙К.
кДж/кг∙К. м3/кг;
м3/кг; кг/м3;
кг/м3; кДж/кг∙К.
кДж/кг∙К.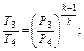
 К;
К; м3/кг;
м3/кг; кг/м3;
кг/м3; кДж/кг∙К.
кДж/кг∙К.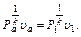
 м3/кг;
м3/кг; К;
К;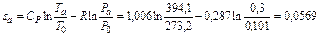 кДж/кг∙К.
кДж/кг∙К.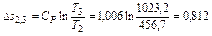 кДж/кг∙К,
кДж/кг∙К, кДж/кг∙К.
кДж/кг∙К. кДж/кг∙К,
кДж/кг∙К, кДж/кг∙К.
кДж/кг∙К.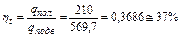 .
. .
.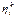 > ηt.
> ηt.