
|
|
Первое начало термодинамикиТермодинамика Параметры состояния и газовые законы
Теоретические основы
Состояние любого вещества принято характеризовать рядом величин, которые в термодинамике называются параметрами состояния. Чаще всего состояние тела определяется следующими параметрами: удельным объемом u, давлением Р и температурой Т. Уравнение состояния идеального газа (уравнение Клапейрона) Связывает между собой все указанные выше параметры (Р, u, Т) и имеет вид: для 1 кг, Рu = RT, для G кг, РV = GRT, для 1 кмоля, Pu = для G кмолей, PV = где Р – абсолютное давление газа, Пa; u - удельный объем газа, м3/кг; R – газовая постоянная для 1 кг газа, Дж/(кгК); Т - абсолютная температура газа, К, Т = 273,2 + t; V – объем газа, м3; G - масса газа, кг; u = mu;
Следует особо отметить, что в уравнении состояния входит только абсолютное давление. Абсолютное давление определяется из отношения Рабс=Рман+ В, где Рман - давление газа по манометру; B – атмосферное (барометрическое) давление. Кроме того, при решении практических задач пользуются следующими законами идеальных газов: Закон Бойля – Мариотта – устанавливает зависимость давления и удельного объема газа при постоянной температуре (Т – idem) Р1υ1= Р2 υ2 или Закон Гей–Люссака при постоянном давлении (P – idem) объем газа при нагревании изменяется прямопропорционально повышению температуры υ = υ0 (1 + αt), где υ – удельный объем при температуре t 0C,υ0 - удельный объем газа при температуре t =0C,α -температурный коэффициент объемного расширения идеальных газов при t = 0 0Cодинаковый для различных газов и сохраняющий одно и тоже значение α=1/273,16 1/К. Или этот закон можно записать в виде:
Примеры решения задач Пример 3.1.1. Баллон с метаном емкостью 100 л находится под давлением 10 МПа при t = 15°С. После израсходования части метана давление понизилось до 7 МПа, а температура упала до t = 10°С. Определить массу израсходованного газа. Решение Из уравнения состояния PV = GRT находим, что до расходования метана его масса в баллоне была равна
После израсходования части газа масса метана в баллоне будет равна
Следовательно, расход метана составит
Пример 3.1.2. Определить удельный объем пропана как идеального газа при следующих условиях: температура газа t = 20°С, манометрическое (избыточное) давление газа в баллоне 5,6 МПа. Абсолютное давление газа в помещении равно В = 0,099 МПа= 99,0 кПа.
Решение Абсолютное давление газа в баллоне
Удельная газовая постоянная пропана
Абсолютная температура газа Т = 273,2 + 20 - 293,2 К. Удельный объем пропана в рассматриваемых условиях
Удельный молярный объем пропана при тех же условиях равен
или, что то же самое,
Пример 3.1.3. Газ при давлении 5 ат (Р1) занимает объем, равный 60 м3 (V1). Какой объем займет газ при 15 ат (Р2) и той же температуре? Решение Согласно закону Бойля-Мариотта при Т=const P2V2=P1V1 Следовательно:
Пример 3.1.4. Коксовый газ, образовавшийся в камере коксовой печи, охладился с 1000 до 500С. Во сколько раз уменьшился объем коксового газа, если давление его не изменилось? Решение Исходя из закона Гей-Люссака при P=const можно записать
Откуда, принимая конечный объем за 1, получим
Пример 3.1.5. Под давлением 100 кПа и при температуре 1230С находится 4,2 кг метана. Какой объем занимает метан? Решение Для G кг газа по уравнению Клапейрона-Менделеева получим:
где Задачи для самостоятельного решения
Задача 3.1.1. В цилиндре с подвижным поршнем находится 1 часть кислорода и 1 часть метана в состоянии термодинамического равновесия. Определить соотношение объемов. Ответ: 0,5. Задача 3.1.2. Компрессор подает кислород в резервуар емкостью 3 м3. Избыточное давление его увеличивается от 0,1 до 6 ат, а температура от -15 оС до +5 оС. Определить количество закачанного кислорода, если барометрическое давление 745 мм рт. ст. Ответ: 21,7 кг. Задача 3.1.3. Сжатый воздух в баллоне имеет температуру t = 15 oС, давление 4,8 МПа. Во время пожара температура воздуха поднялась до 450 оС. Взорвется ли баллон, если известно, что при этой температуре он может выдержать давление не более 9,8 МПа. Задача 3.1.4. Баллон с кислородом емкостью 20 л находится под давлением 10 МПа при t = 15 oС. После израсходования части кислорода давление понизилось до 7,6 МПа, а температура упала до 10oС. Определить массу израсходованного кислорода. Ответ: 0,606 кг. Задача 3.1.5. В баллоне с метаном первоначальное давление составляло 320 кПа. При той же температуре повысили давление в баллоне до 5000 кПа. Во сколько раз изменится плотность метана? Ответ: в 15,6 раза. Задача 3.1.6. В газгольдер при температуре 270С закачано 100000 м3 коксового газа. Какой объем будет занимать указанное количество газа при температуре 2700С. Ответ: 181000 м3. Задача 3.1.7. Какова масса 10 м3 водорода, 10 м3 азота и 10 м3 метана при 10 ат и 1000С? Ответ: H2=6,37 кг; N2 = 88,5 кг; CH4 = 50,6 кг. Газовые смеси Теоретические основы Характерной особенностью газовых смесей является то, что каждый входящий в смесь газ или, как обычно говорят, компонент ведет себя так, как будто других составляющих смеси газов не существует, то есть он распространяется по всему доступному для него объему. Примером такой смеси служит природный газ, компонентами которого являются метан СН4, этан С2Н6, пропан С3Н8, бутан С4Н10 и другие углеводороды смеси. Решение задач на смеси сводится, главным образом, к определению массовых и молярных концентраций компонентов (тi, ri), определению
средней молекулярной массы смеси (μi), теплоемкостей смеси (Cpm, Cvm), газовой постоянной (Rm), средней температуры смеси (Tm). Состав газовой смеси определяется количеством каждого из газов, входящих в смесь, и может быть задан массовыми или объёмными долями. Массовая доля определяется отношением массы отдельного газа, входящего в смесь, к массе всей смеси:
где M1 , M2 , M3, …,Mn – массы отдельных газов и M – масса всей смеси. Объёмной долей газа называют отношение объёма каждого компонента, входящего в смесь, к объёму всей газовой смеси, при условии, что объём каждого компонента, отнесён к давлению и температуре (приведённый объём):
где V1 ,V2,V3,…Vn – приведённые объёмы компонентов газов, входящих в смесь; V – общий объём газовой смеси. Очевидно, что
а также
Для перевода массовых долей в объёмные пользуются формулой
Объёмные доли переводят в массовые по формуле
Плотность смеси определяют из выражения
или, если известен массовый состав, по формуле
Удельный объём смеси представляет величину обратную, поэтому, если дан объёмный состав смеси, то
Если же известен массовый состав, то
Из уравнения (3.1.4) легко получить так называемой кажущейся молекулярной массы газовой смеси
или через массовый состав
Газовую постоянную смеси газов (Rсм) можно выразить или через газовые постоянные отдельных компонентов, входящих в смесь, или через кажущуюся молекулярную массу смеси
или
Связь между давлением газовой смеси и парциальными давлениями отдельных компонентов, входящих в смесь, устанавливается следующей зависимостью (закон Дальтона), легко получаемый из основного уравнения кинетической теории газов:
где p – общее давление газовой смеси; p1, p2, …, pn – парциальные давления отдельных компонентов, входящих в смесь. В табл. 3.1.1 даны формулы для расчёта газовых смесей.
Таблица 3.1.1 Формулы для расчёта газовых смесей
Парциальные давления определяются проще всего, если известны объёмные доли отдельных компонентов входящих в смесь;
или вообще
где pi – парциальное давление любого газа, входящего в смесь. Если известны массовые доли, то парциальное давление любого газа, входящего в смесь,
Примеры решения задач
Пример 3.1.6. По данным анализа установлен следующий объемный состав природного газа:
Определить среднюю молекулярную массу природного газа μт, плотность газа в нормальных условиях ρ, массовые концентрации компонентов тi, их парциальные давления Pi; средние теплоемкости Cpm, Cvm и показатель адиабаты k. Решение Молекулярные массы составляющих смесь газов равны (по данным физических характеристик компонентов газа из справочных таблиц):
Молекулярная масса природного газа определяется по уравнению
где μi — молекулярная масса компонентов смеси, CH4, C2H6, C3H8 и т. д.; ri — молярная (или объемная) концентрация компонентов смеси, определяемая как отношение объема компонента к объему смеси; тi -массовая концентрация компонентов смеси, определяемая как отношение массы данного компонента к массе смеси в целом. Так как в условии задачи дан объемный состав газа, то удобнее воспользоваться первым уравнением соотношения (3.1.13)
Плотность газа при нормальных условиях (0°С и 0,1 МПа) можно определить из уравнения Клапейрона Рυ=Р/ρ=R/T или из закона Авогадро, утверждающего, что удельный молярный объем газа в нормальных условиях величина постоянная и равна
По уравнению Клапейрона при t = 0°C и Р = 0,1 МПа
Массовые и объемные концентрации газа связаны между собой соотношением
отсюда
Следовательно, массовые концентрации отдельных компонентов смеси равны:
Так что массовый состав газа в процентах равен:
Сумма массовых концентраций, как и молярных (объемных), равна единице:
Парциальные давления отдельных компонентов газа определяются по закону Дальтона из соотношения
Так что давление метана CH4, этана C2H6 и т. д. в смеси равно:
Сумма парциальных давлений равна давлению смеси
Средняя теплоемкость смеси определяется по уравнениям: массовая теплоемкость смеси
молярная теплоемкость смеси
где При температуре 0 °С и давлении 0,1 МПа можно принять, что теплоемкость метана
Молярная теплоемкость смеси газов при постоянном давлении
Из уравнения Майера
Из сопоставления численных значений теплоемкостей можно определить показатель адиабаты природного газа указанного состава (как идеального газа)
Пример 3.1.7. Критическая температура н-бутана Ткр=425,2 К и критическое давление Ркр=37,5 атм. Определить удельный объем н-бутана при температуре 80 0С и давлении 10 кг/см2. Решение а) Определяем приведенную температуру и приведенное давление
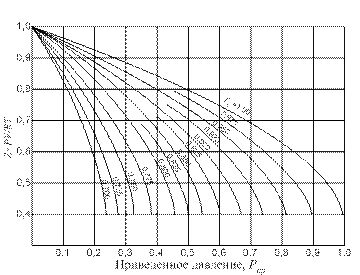
б) По графику рис. 3.1.2 определяем коэффициент сжимаемости z=0,825. в) удельный объем определяем из уравнения
Пример 3.1.8. Определить вязкость водорода и вязкость двуокиси углерода при температуре 200 0С и нормальном давлении. Решение Вязкость названных газов определяем по уравнению Сутерланда
Таблица 3.1.2 Значение коэффициента С в уравнении Сутерланда для различных газов
Вязкость водорода и двуокиси углерода при нормальной температуре равна: водорода 84∙10-7н∙сек/м2 и двуокиси углерода 136,75∙10-7 н∙сек/м2, а из табл. 3.1.2 значение равно 73 и 254. Вязкость Н2 при 2000С: Тем же приемом определяем для СО2 η = 225,8∙10-7 н∙сек/м2. Пример 3.1.9. Атмосферный воздух имеет примерно следующий массовый состав: тО2=23,2%; тN2=76,8%. Определить объемный состав воздуха, его газовую постоянную, кажущуюся молекулярную массу и парциальные давления кислорода и азота, если давление воздуха по барометру р=101325 Па. Решение По уравнению получаем
Газовую постоянную воздуха находим по уравнению
=0,232∙260+0,768∙295=287 Дж/(кг∙К). Кажущуюся молекулярную массу смеси определяем из уравнения
=0,21∙32+0,79∙28,02=28,9, или из уравнения
Отсюда
Парциальные давления получим из уравнения рi=rip, следовательно рО2=rО2 p=0,21∙101325=21278 Па; рN2=rN2 p=0,79∙101325=80047 Па.
Задачи для самостоятельного решения
Задача 3.1.8.Баллон объемом V1=0,35 м3, содержащий метан, соединили с баллоном объемом V2=0,15 м3, содержащим этан. Определить удельную газовую постоянную смеси, а также парциальные давления компонентов, если давление смеси в целом равно Р = 0,5 МПа. Ответ: сумма парциальных давлений компонентов равна общему давлению (контрольное уравнение)
Задача 3.1.9. При сгорании 1 кг природного газа образуются продукты сгорания следующего массового состава: Определить молекулярную массу смеси, ее газовую постоянную, показатель адиабаты для смеси компонентов. Ответ: μт=30,58 кг/кмоль; R=271,9 Дж/кг∙К; К=1,37. Задача 3.1.10.В коллекторе смешивается несколько газов: углекислый газ СО2 с температурой 450°С и массовым расходом 5 кг/с, окись углерода СО с температурой 400°С и массовым расходом 2 кг/с и азот N2 с температурой 350°С и массовым расходом 8 кг/с. После смешения смесь газов идет на нагрев воды; при этом смесь охлаждается до температуры 200°С. Определить среднюю температуру смеси и количество тепла, отданное воде в условиях постоянного давления (рис. 3.1.1),
Рис. 3.1.1. Принципиальная коллекторная схема смешения газов (Р =idem)
Ответ: tm=389оС; Q=297,7 кВт. Задача 3.1.11. Имеются газы: метан - 0,8 м3 при 10 ат (0,98 МПа), этан - 0,6 м3 при ат (0,59 МПа) и пропан - 0,4 м3 при 4 ат (0,39 МПа). Найти давление их смеси в объеме 1 м3 и молярные концентрации. Задача 3.1.12. Определить, сколько углекислоты (СО2) может раствориться в 15 т воды при нормальном давлении и температуре 20 0С. Задача 3.1.13. Объем газа, собранного над водой при 20 0С и барометрическом давлении 750 мм рт. ст., равен 1,2 м3. Какой объем займет указанное количество газа при нормальных условиях? Ответ: V0=1,08 нм3. Задача 3.1.14. Определить приведенные температуры и приведенное давление водорода и метана при температуре 1000С и давлении 21 кг/см2 (2,06 МПа) (рис. 3.1.2). Задача 3.1.15.Газовая смесь находится под давлением 3 МПа. Объемная концентрация компонентов смеси: r1=0,4; r2=0,2; r3=0,3; r4=0,1. Определить парциальное давление этих компонентов в смеси. Ответ: Р=3 Мн/м3. Задача 3.1.16. Газовая смесь, состоящая из метана - 80%; этана - 8,5%; этилена - 4.8%; пропана - 6% и пропилена - 0,7%, сжата при температуре 600С до 40 ат. Определить плотность газовой смеси. Ответ: ρ = 27,3 кг/м3. Задача 3.1.17.Определить коэффициент теплового расширения пропилена в пределах температур от -20 до +200С. Задача 3.1.18. Газовая смесь состоит из метана - 80%; этана - 10%; пропана - 6,4%; н-бутана - 3,6%. Определить динамическую вязкость смеси при нормальных условиях.
Рис. 3.1.2. Зависимость приведенной температуры от приведенного давления
Задача 3.1.19. Определить газовую постоянную смеси газов, состоящей из 1 м3 генераторного газа и 1,5 м3 воздуха, взятых при нормальных условиях, и найти парциальные давления составляющих смеси. Плотность генераторного газа ρ принять равной 1,2 кг/м3. Ответ: Rсм=295 Дж/(кг∙К); рг.г=0,4 рсм; рвозд=0,6 рсм. Задача 3.1.20. Имеется смесь газов под давлением 30 ат (2,94 МПа). Молярная концентрация первого газа r1=0,4; второго r2=0,2; третьего r3=0,3 и четвертого r4=0,1. Определить парциальное давление этих компонентов в смеси. Ответ: Р1=12 ат (1,18 МПа); Р2=6 ат (0,59 МПа); Р3=9 ат (0,88 МПа); Р4=3 ат (0,29 МПа). Задача 3.1.21. Рассчитать состав растворенного в воде при температуре 0 0С газа и давлении 1 ат, состоящего из 90% метана и 10% этана. Ответ: метана 4,91 см3; этана 0,99 см3. Задача 3.1.21. Определить объем газа при нормальных условиях, если его объем при температуре 125 0С и давление 15 ат составляет 100 м3. Ответ: 1030 нм3. Задача 3.1.22. Имеется газ следующего состава (в весовых процентах): метана 85%; этана 8%; пропана - 5% и н-бутана - 2%. Определить среднекритическую температуру и среднекритическое давление. Ответ: Ткр=-59,5 0С; Ркр=45,9 кг/см2. Первое начало термодинамики (Закон сохранения энергии) Теоретические основы Первое начало, как математическое выражение закона сохранения энергии, в технической термодинамике записывается в форме
или для одного 1 кг вещества
где Q*1,2 — тепло, подведенное к газу со стороны или отведенное от газа. Если тепло подводится, то Q*1,2, q*1,2 имеют знак плюс, если отводится — минус; и2-и1 — изменение внутренней энергии (и2–и1) или его энтальпии (i2–i1); i*1,2, w*1,2 — соответственно термодинамическая и потенциальная работа, подводимая к газу извне, или совершаемая газом. Если работа подводится к газу, то она имеет знак минус, если работа совершается газом, то она имеет знак плюс. Уравнения (3.1.21) и (3.1.22) называются уравнениями первого начала термодинамики по внешнему балансу тепла и работы, то есть в этих уравнениях учитывается только тепло, которое подведено извне, или отведено. Здесь не учитываются все необратимые потери, которые всегда имеют место в реальных процессах. Можно сказать, что уравнения (3.1.21) и (3.1.22) справедливы только для обратимых (идеальных) процессов, без учета каких-либо потерь в процессах. Для реальных процессов первое начало термодинамики для 1 кг газа записывается в форме
где q*1,2 - подведенное (или отведенное) к газу извне тепло; q**1,2 - тепло внутреннего теплообмена, возникшее в необратимых (реальных) процессах, в частности, в результате трения; q1,2 - так называемое приведенное тепло, определяемое как сумма внешнего (q*1,2) и внутреннего (q**1,2) теплообмена:
Уравнение (3.1.24) называется уравнением первого начала термодинамики по балансу рабочего тела и оно справедливо для всех реальных процессов. Для обратимых процессов, когда q**1,2 = 0, уравнение (3.1.23) переходит в уравнение первого начала термодинамики по внешнему балансу тепла и работы (уравнения 3.1.21 – 3.1.22). Обычно задачи на первое начало термодинамики решают исходя из того, что все процессы обратимые (q**1,2 = 0). При решении задач на первое начало термодинамики применительно к теплосиловым установкам, работающим по тем или иным циклам, исходят также из условия полного превращения тепла в работу (для обратимых процессов)
Уравнение (3.1.25) непосредственно следует из уравнений (3.1.21) и (3.1.23) применительно к круговым процессам (циклам), когда
Примеры решения задач
Пример 3.1.10. В газотурбинной установке за сутки ее работы на компрессорной станции сожжено 37∙103 м3 природного газа, имеющего теплоту сгорания QHP = 46000 кДж/кг. Определить среднюю мощность газотурбинной установки, если КПД ее составлял ηt = 23%. Плотность природного газа в данном случае равна ρ = 0,78 кг/м3. Решение 1. Массовый расход топливного газа за сутки по газотурбинной установке равен
2. Количество тепла, превращенного газотурбинной установкой в работу, за сутки
3. Эквивалентная этому количеству тепла работа в кВт∙ч составляет
4. Средняя мощность газотурбинной установки за сутки составит
Задачи для самостоятельного решения
Задача 3.1.23. Газотурбинная установка ГТК-10 мощностью 10000 кВт работает с КПД, равным ηt = 0,25. Определить часовой расход топлива по установке, если теплота сгорания его равна QHP = 46000 кДж/кг. Ответ: В = 3130 кг/ч. Задача 3.1.24.При испытании поршневого двигателя для определения его мощности, двигатель затормаживают. При этом работа, произведенная двигателем, расходуется на преодоление сил трения и превращается в тепло, часть которого (~20%) рассеивается в окружающей среде, а остальная часть отводится охлаждающей тормоз водой. Сколько воды необходимо подводить к тормозу за 1 ч, если крутящий момент двигателя равен Mкр = 2000 Дж, число оборотов двигателя n = 1600 об/мин, а допустимое повышение температуры воды равно Δt=t2-t1=35 oC. Теплоемкость воды С = 4,19 кДж/кг°С. Ответ: G=6588 кг/ч. Задача 3.1.25.При движении природного газа по трубопроводу его параметры изменяются от t1 = 50°С и P1 = 5,5 МПа до t2 = 20°C и P2 = 3,1 МПа. Средняя молекулярная масса газа μm = 18. Средняя теплоемкость газа Cpm = 1,628 кДж/кг°С. Считая газ идеальным и принимая во внимание, что внешняя полезная работа на участке трубопровода равна нулю (w*12=0), определить удельную величину внешнего (q*12) и внутреннего теплообмена (q**12). Ответ: q*12=48,8 кДж/кг; q**12=82,8 кДж/кг. Задача 3.1.26. 2м3 воздуха при давлении 0,5 МПа и температуре 50 0C смешиваются с 10 м3 воздуха при давлении 0,2 МПа и температуре 100 0C. Определить давление и температуру смеси. Ответ: t = 82 0C; ρcм= 0,25 МПа. Задача 3.1.27. Найти изменения внутренней энергии 2м3 воздуха, если температура его понижается от t1 = 250 0C до t2 = 70 0С. Зависимость теплоемкости от температуры принять линейной. Начальное давление воздуха ρ1 = 0,6 МПа. Ответ: ΔU = - 1063 кДж. Задача 3.1.28. К газу, заключенному в цилиндре с подвижным поршнем, подводиться из вне 100 кДж теплоты. Величина произведенной работы при этом составляет 115 кДж. Определить изменение внутренней энергии газа, если количество его равно 0,8 кг. Ответ: ΔU = - 18,2 кДж. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
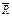 T,
T,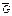
 = mu - удельный объем 1 кмоля газа, м3/кмоль,
= mu - удельный объем 1 кмоля газа, м3/кмоль,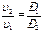
 .
. кг;
кг;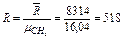 Дж/(кг∙К).
Дж/(кг∙К).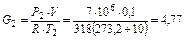 кг.
кг.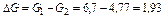 кг.
кг.
 МПа.
МПа. Дж/(кг∙К).
Дж/(кг∙К).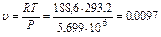 м3/кг.
м3/кг. м3/кмоль,
м3/кмоль,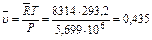 м3/кмоль.
м3/кмоль.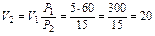 м3.
м3.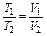
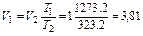 раза.
раза.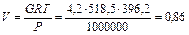 м3;
м3;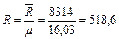 Дж/кг∙К,
Дж/кг∙К,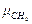 =16,03.
=16,03.

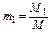 ,
, 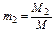 ,
, 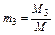 , …,
, …,  ,
,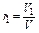 ,
, 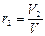 ,
, 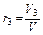 , …,
, …, 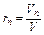 ,
,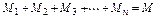 ;
;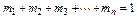 ,
,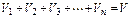 ;
;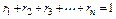 .
.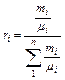 . (3.1.2)
. (3.1.2)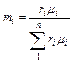 . (3.1.3)
. (3.1.3)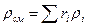 , кг/м3 (3.1.4)
, кг/м3 (3.1.4)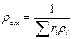 , кг/м3 (3.1.5)
, кг/м3 (3.1.5) , м3/кг (3.1.6)
, м3/кг (3.1.6) , м3/кг (3.1.7)
, м3/кг (3.1.7)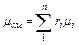 (3.1.8)
(3.1.8) . (3.1.9)
. (3.1.9) , Дж/(кг∙К) (3.1.10)
, Дж/(кг∙К) (3.1.10)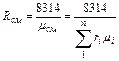 , Дж/(кг∙К) (3.1.11)
, Дж/(кг∙К) (3.1.11)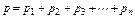 ,
,



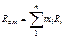


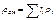

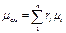

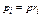
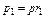 ,
,  и т.д.
и т.д.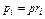 (3.1.12)
(3.1.12)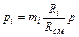 .
.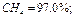

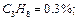
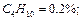
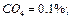
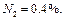
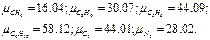
 , (3.1.13)
, (3.1.13)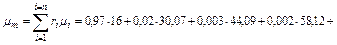
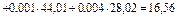 кг/кмоль.
кг/кмоль. м3/кмоль,
м3/кмоль,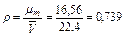 кг/м3.
кг/м3.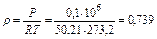 кг/м3,
кг/м3, Дж/(кг∙К).
Дж/(кг∙К). (3.1.14)
(3.1.14) (3.1.15)
(3.1.15)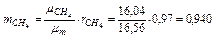 ,
,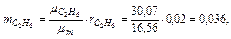

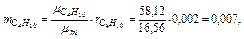
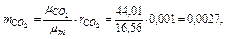
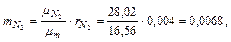
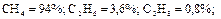
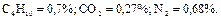
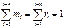 (3.1.17)
(3.1.17) (3.1.18)
(3.1.18)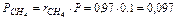 МПа,
МПа,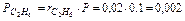 МПа,
МПа,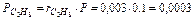 МПа,
МПа,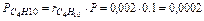 МПа,
МПа, МПа,
МПа,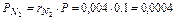 МПа.
МПа.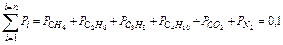 МПа.
МПа. (3.1.19)
(3.1.19)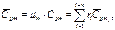 (3.1.20)
(3.1.20)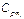 — массовая теплоемкость компонентов смеси при данной температуре;
— массовая теплоемкость компонентов смеси при данной температуре; 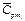 — молярная теплоёмкость компонентов смеси при данной температуре.
— молярная теплоёмкость компонентов смеси при данной температуре.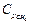 = 2,17 кДж/кг∙К, этана
= 2,17 кДж/кг∙К, этана  = 1,65 кДж/кг∙К, пропана
= 1,65 кДж/кг∙К, пропана 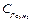 = 1,56кДж/кг∙К, бутана
= 1,56кДж/кг∙К, бутана  = 1,58 кДж/кг∙К, углекислого газа
= 1,58 кДж/кг∙К, углекислого газа  = 0,815 кДж/кг∙К, азота
= 0,815 кДж/кг∙К, азота 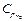 =1,039 кДж/кг∙К. Следовательно, массовая теплоемкость смеси (при постоянном давлении) равна
=1,039 кДж/кг∙К. Следовательно, массовая теплоемкость смеси (при постоянном давлении) равна
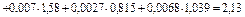 кДж/кг∙К.
кДж/кг∙К. кДж/кмоль∙К.
кДж/кмоль∙К.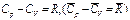 можно найти теплоемкости смеси при постоянном объеме
можно найти теплоемкости смеси при постоянном объеме 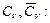
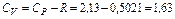 кДж/кг∙К,
кДж/кг∙К, кДж/кг∙К.
кДж/кг∙К.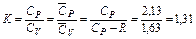 .
.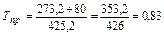 ,
,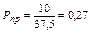 .
. откуда
откуда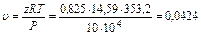 м3/кг.
м3/кг.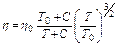
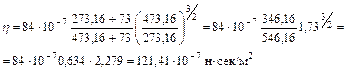
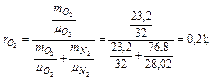
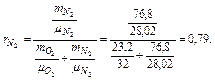
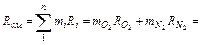
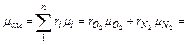
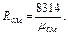
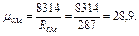
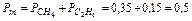 МПа.
МПа.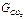 = 3,5 кг,
= 3,5 кг, 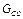 = 1,06 кг;
= 1,06 кг; 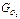 = 1,4 кг и
= 1,4 кг и 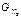 = 12,1 кг.
= 12,1 кг.
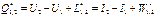 , (3.1.21)
, (3.1.21)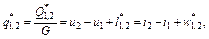 (3.1.22)
(3.1.22)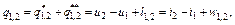 (3.1.23)
(3.1.23)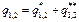 (3.1.24)
(3.1.24)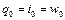 (3.1.25)
(3.1.25)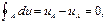 (3.1.26)
(3.1.26)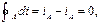 (3.1.27)
(3.1.27)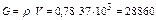 кг.
кг.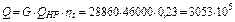 кДж.
кДж.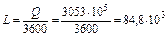 кВт∙ч. (3.1.28)
кВт∙ч. (3.1.28)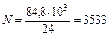 кВт.
кВт.