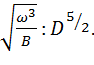|
|
РАСЧЕТ КАНАЛОВ, ИМЕЮЩИХ ЗАМКНУТЫЙ ПОПЕРЕЧНЫЙ ПРОФИЛЬПримерами каналов, имеющих замкнутый профиль, могут являться : a) канализационные трубы, б) дренажные трубы, в) гидротехнические туннели. Эти водотоки работают как безнапорные (см. рис. 6-3,г). Поэтому с гидравлической точки зрения они ничем не отличаются от открытых каналов. 1°. Канализационные трубы. Канализационные трубы могут быть различного поперечного сечения. На рис. 6-11 для примера представлены: круглое поперечное сечение (схема а); овоидальноесечение — «нормальный тип 3/2» (схема б); это сечение применяется, когда в процессе эксплуатации имеются значительные колебания расхода Q; лотковое сечение (схема в), применяемое при так называемой ливневой канализации.
Рис. 6-11. Сечения канализационных труб Обозначим через h глубину наполнения трубы и через D полную ее высоту. Отношение
называется степенью наполнения. В практике обычно принимают:
Замкнутые профили характеризуются следующей особенностью.
Рис. 6-12. Изменение Q и υс изменением h (при i =const) для замкнутого профиля Представим на рис. 6-12 замкнутый профиль любого очертания. Предположим, что при i = const глубина наполнения этого профиля изменяется в пределах от h = 0 до h = D. При этом средняя скорость v и расход Q будут также изменяться от нуля до некоторых значений vu и Qн, отвечающих полному наполнению рассматриваемого канала. Существенным является то обстоятельство, что функции υ=f1(h); Q =f2(h) в случае замкнутых профилей имеют максимум, чего не наблюдаем для обычных открытых русел. Непосредственными подсчетами по формуле Шези было показано, что: а) глубина h1, отвечающая υмакс, лежит обычно в пределах:
б) глубина же h2, при которой мы получаем Qмакс, лежит обычно в пре-
Как видно, некоторый расход Q, находящийся в пределах
имеет место в случае равномерного движения воды в трубе при двух различных глубинах: h' < h2 и h" > h2. Таким образом, при расходе, лежащем в указанных пределах, возможно изменение условий протекания воды: глубина h' может «переключаться» в глубину h" и наоборот. Наличие максимума расхода Q=𝜔υ в случае замкнутых профилей с физической точки зрения может быть объяснено следующим образом: представим себе наполнение трубы h только немногим меньше высоты трубы D; дадим далее величине h малое приращение δh; при таком приращении глубины h благодаря тому, что горизонт воды стоит почти у самого замка свода, получим ничтожно малое приращение живого сечения 𝜔, однако смоченный периметр, определяющий поверхность трения, увеличится значительно. В результате увеличения χ скорость v уменьшится, и это уменьшение скорости будет более существенным, чем увеличение 𝜔. Следует, однако, иметь в виду, что все сказанное выше получается в результате формального анализа зависимости Шези, без учета того обстоятельства, что между свободной поверхностью и замком свода имеется воздушная прослойка (прослойка «газообразной жидкости»), которая тоже приходит в движение при движении воды в трубе. Наличие этой воздушной прослойки, обусловливающей возникновение на свободной поверхности потока соответствующих сил трения, в некоторой мере искажает описанную выше картину движения воды. Обратимся к расчету канализационных труб. Коэффициент шероховатости п для канализационных труб принимается равным
обычно вне зависимости от материала, из которого выполнены стенки труб, так как такие трубы с течением времени покрываются осадками, что в значительной мере сглаживает различие шероховатостей разных материалов. В связи с тем, что величины 𝜔 и χ для канализационных труб определять по тем или иным геометрическим формулам затруднительно (эти формулы в данном случае получают слишком сложный вид), при выполнении практических расчетов приходится пользоваться различными расчетными таблицами и графиками, приводимыми в справочной литературе. Таблица 6-2 Значения Кп и Wпдля круглых труб при п = 0,013 по Гангилье-Куттеру
Поясним здесь для примера только расчет кругового профиля. Задачи, с которыми приходится сталкиваться при расчете канализационных труб, следующие: 1) даны тип поперечного профиля и его размеры, а также величины а и i требуется найти расход Q; 2) даны тип профиля и его размеры, а также величины а и Q; требуется найти уклон дна i и т. п. Решение таких задач выполняется следующим образом. 1. Обозначим через Кп и Wn модули расхода и скорости, отвечающие полному заполнению трубы, когда h = D и а = 1. В приводимой табл. 6-2 даются величины Кп и Wn в зависимости от D, где D в данном случае является диаметром трубы:
2. Введем обозначения
где К и W — модули расхода и скорости, отвечающие действительной глубине h, имеющейся в трубе.
Рис, 6-13. К расчету круглых канализационных труб
Оказывается, что величины М и N практически не зависят от размеров рассматриваемой трубы; как показывают соответствующие подсчеты, величины М и N зависят только от формы поперечного профиля трубы и от степени наполнения трубы а. Имея это в виду, в литературе даются графики для разных форм поперечного профиля труб, в частности, для кругового профиля (рис. .6-13):
3. Для расчета труб имеем известные формулы:
Эти формулы можно представить в виде
или в виде
Пользуясь формулами (6-47), а также указанными выше таблицами и графиками, и ведем расчет. Например, требуется найти для трубы кругового профиля расход Q, если известны D, a, i. Для решения этой задачи поступаем следующим образом: а) для заданного D по приведенной таблице находим Кп и Wп; б) для заданного а по графику на рис. 6-13 находим М и N (более точно в) наконец, по формулам (6-47) вычисляем v, а также Q. 2°. Дренажные трубы.Дренажные трубы применяют, в частности, для осушения земель. На рис. 6-14, а представлена сеть дренажных труб в плане; на рис. 6-14,б дается разрез по линии АВ. Как видно из чертежа на рис. 6-14,б грунтовая вода поступает в дренажные трубы через отверстия, имеющиеся в их стенках, причем горизонт грунтовых вод снижается до положения, показанного пунктиром. В результате получаем осушение грунта на глубину у. Грунтовая вода, попавшая в трубы, течет по ним и затем сбрасывается в водоприемник. Очевидно, уклон и размеры поперечного сечения труб должны быть достаточными для пропуска расхода воды, поступающей из грунта в трубы (для гидравлического расчета труб этот расход следует считать заданным), величина этого расхода устанавливается на основании расчета движения грунтовых вод (см. гл. 17).
Рис. 6-15. Дренажная труба
Расчет дренажных труб ведется так же, как и расчет канализационных труб, но при сплошном их заполнении (рис. 6-15), т. е. величина а для дренажных труб принимается а = 1; (6-48) однако дренажная труба все же считается безнапорной; давление в точке А принимается равным атмосферному.
Рис. 6-14. Дренаж для осушения земли
Для случая круглых труб, которые часто применяются для устройства дренажа, имеем следующие расчетные зависимости, написанные с учетом (6-48):
Коэффициент Шези Синогда определяют здесь по эмпирической формуле Куттера. Эта формула имеет вид:
где к — особый коэффициент шероховатости, принимаемый для гончарных труб равным 0,27; R и D — в м; v — в м/с. Допустимые скорости для гончарных труб обычно принимают равными: а) минимальную скорость υмин = 0,15 б) максимальную скорость υмакс =1,0 м/с.
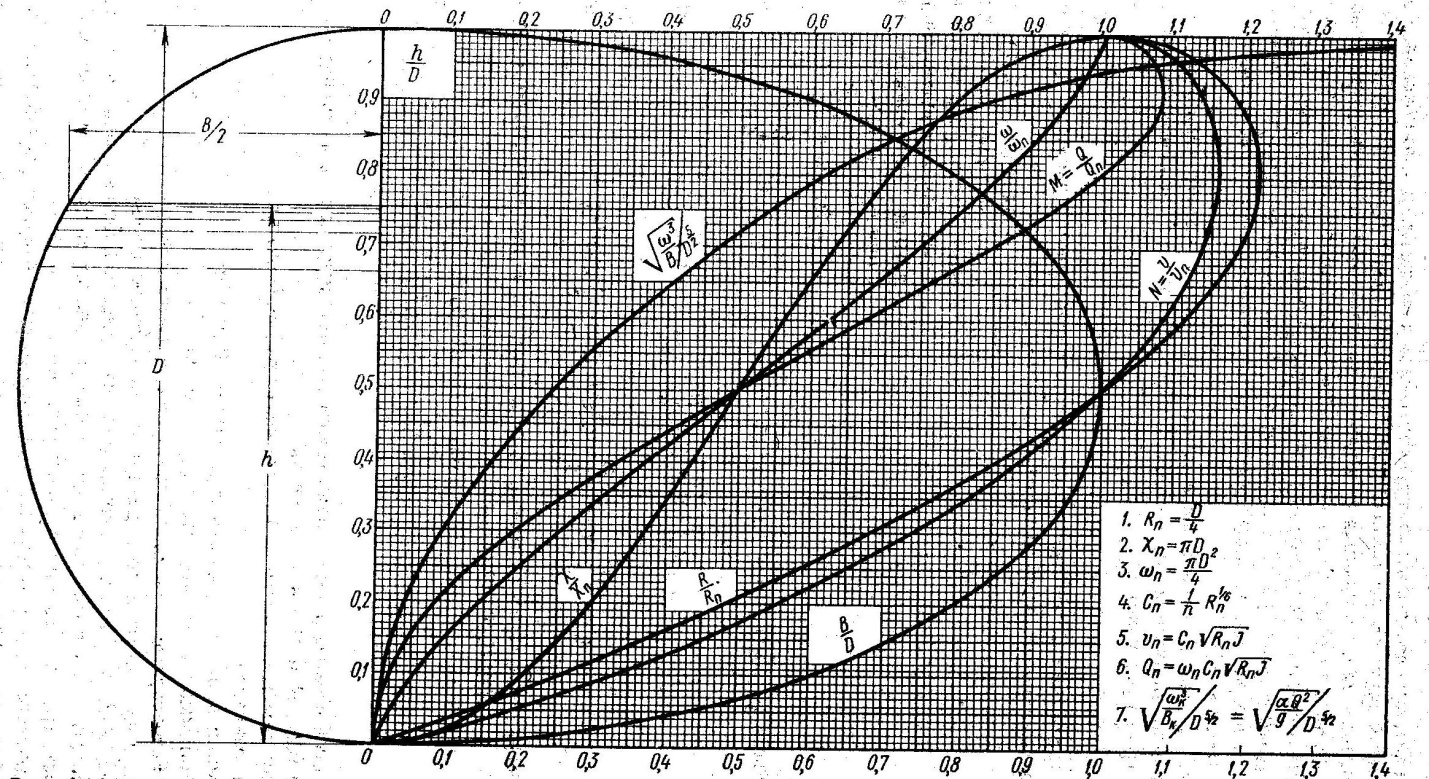
Рис 6-16 График для определения гидравлических элементов безнапорного потока в цилиндрическом канале круглого поперечно сечения
На рис. 6-16 приводится график, служащий для гидравлического расчета безнапорных гидротехнических туннелей круглого поперечного сечения. На этом графике, построенном в безразмерных координатах, индексом «п» отмечены величины, относящиеся к случаю, когда h (глубина наполнения) равна D (диаметр туннеля), т. е. когда имеем полное наполнение туннеля. По вертикальной оси графика отложено относительное наполнение туннеля h/D; по горизонтальной оси — величины М и N (см. выше п. 1°), а также величины:
В экспликации к графику приведены отдельные формулы, служащие для определения Rп, χп, 𝜔п, Сп, vn, Qn; кроме того, дается формула (см. п. 7 экспликации), исходя из которой можно найти для круглого поперечного сечения канала так называемую критическую глубину (об этом см. далее § 7-5). Как видно, при помощи данного графика, зная Rп, χп, 𝜔п, Сп, vn, Qn, легко найти также величины R, χ, 𝜔, В, v, Q, К, W для любого наполнения круглого туннеля. Необходимо однако отметить, что расчет гидротехнических туннелей на равномерное движение (с использованием формул Шези при коэффициенте шероховатости n = const) является иногда несколько условным. Дело в том, что длина таких туннелей часто бывает соизмерима с длиной так называемого начального участка [см. формулу (4-66)], в пределах которого имеет место неравномерное движение воды.

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|

 (6-38)
(6-38) (6-39)
(6-39)
 (6-40)
(6-40) (6-41)
(6-41)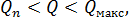
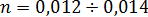
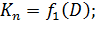
 (6-42)
(6-42)
 (6-43)
(6-43)

 (6-44)
(6-44)
 (6-45)
(6-45)
 (6-46)
(6-46)
 (6-47)
(6-47)




 (6-49)
(6-49) (6-50)
(6-50) (6-51)
(6-51)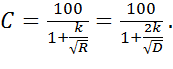 (6-52)
(6-52)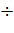 0,20 м/с;
0,20 м/с;