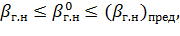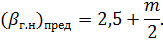|
|
ГИДРАВЛИЧЕСКИ НАИВЫГОДНЕЙШИЙ ПОПЕРЕЧНЫЙ ПРОФИЛЬ ТРАПЕЦЕИДАЛЬНОГО КАНАЛАГЛАВА ШЕСТАЯ
РАВНОМЕРНОЕ БЕЗНАПОРНОЕ УСТАНОВИВШЕЕСЯ ДВИЖЕНИЕ ВОДЫ В КАНАЛАХ
§ 6-1. ПРЕДВАРИТЕЛЬНЫЕ ЗАМЕЧАНИЯ Ограничимся рассмотрением только турбулентного движения воды, относящегося к квадратичной области сопротивления (в доквадратичной области обычные каналы, встречающиеся в гидротехнической практике, могут работать относительно редко). На рис. 3-29 (см. § 3-21)была представлена схема рассматриваемого движения, из которой видно, что уклон дна канала поскольку величина l измеряется вдоль наклонной линии дна канала (угол В том случае, когда канал имеет, в частности, земляное русло (что особенно часто встречается в практике) скорости vв канале назначаются сравнительно малыми (чтобы не получить размыва грунта); при этом и уклоны дна земляных каналов получаются также небольшими. В связи с этим для земляных (и некоторых других) каналов можно считать, что
Как видно, здесь мы можем поступать следующим образом: а) расстояние l - измерять по горизонтали, б) живые же сечения потока считать вертикальными, измеряя глубины h — по вертикали (см. рис. 6-1).Очевидно, в этом случае рис. 6-1(на котором дно канала показано с большим уклоном) следует рассматривать как чертеж, выполненный в искаженном масштабе (вертикальном масштабе — относительно крупном, горизонтальном — относительно мелком; именно поэтому уклон дна канала на этом рисунке получился большим). Ниже мы ограничимся изучением только случая, характеризуемого схемой, представленной на рис. 6-1. Основные зависимости, используемые при расчете таких каналов (когда Je = J = i = tg θ), следующие: (I)
Рис.6-1. Схема (в искаженном масштабе) равномерного движения воды в канале с малым уклоном дна (sin последнюю зависимость, учитывая, что в данном случае hl = а = ад (см. рис. 6-1) и что J переписываем в виде (II) Дополнительно будем пользоваться еще формулами: (III) (IV) (V)
Кроме того, иногда будем применять зависимост
Что касается коэффициента Шези С, то он определяется так, как это было пояснено в § 4-13.
ГИДРАВЛИЧЕСКИЕ ЭЛЕМЕНТЫ ЖИВОГО СЕЧЕНИЯ ПОТОКА В КАНАЛЕ Наиболее часто встречаются поперечные сечения каналов, показанные на рис. 6-2. Приведем ниже формулы, служащие для определения величин 𝜔,χ и R. 1°. Симметричное трапецеидальное поперечное сечение (рис. 6-2, а). Здесь b - ширина канала по дну; h — глубина наполнения канала; величина m, указанная на чертеже, — коэффициент откоса:
где угол ψ (см. чертеж) задают не по соображениям гидравлического расчета, а учитывая устойчивость грунта откоса (если откосы канала образуются нескальным грунтом). Ширина потока поверху:
Величины живого сечения со и смоченного периметра χудобно вычислять по следующим геометрическим зависимостям:
Рис. 6-2. Примеры поперечного сечения каналов
Зная 𝜔 и χ, определяем величину R: Иногда при расчете каналов пользуются понятием относительной ширины канала по дну:
Величины 𝜔 и χ через β выражаются следующим образом:
2°. Прямоугольное поперечное сечение (рис. 6-2,6).Здесь
в случае весьма широкого прямоугольного русла
Рис. 6-3. Примеры поперечного сечения каналов
3°. Треугольное поперечное сечение (рис. 6-2, в). Здесь
4°. Параболическое поперечное сечение (рис. 6-2, г). Уравнение параболы, образующей смоченный периметр, имеет вид:
где p-параметр параболы; оси x и yуказаны на рис. 6-2, г.Для такого русла ширина потока поверху Вможет быть найдена (для заданной глубины h) из уравнения (6-23);
5°. Прочие поперечные сечения.Отметим следующие профили: а) несимметричный профиль (рис. 6-3, а); б) неправильный профиль (рис. 6-3,6); в этом случае, как и в предыдущем, в) составной профиль (рис. 6-3, в); г) замкнутые профили (рис. 6-3,г); здесь имеем так называемый закры-
ГИДРАВЛИЧЕСКИ НАИВЫГОДНЕЙШИЙ ПОПЕРЕЧНЫЙ ПРОФИЛЬ ТРАПЕЦЕИДАЛЬНОГО КАНАЛА
Предположим, что нам заданы: 1) форма поперечного сечения канала — трапецеидальная; 2) коэффициент откоса канала т = т0;3) уклон дна канала i = i0; 4) коэффициент шероховатости п=п0; 5) расход Q = Q0.
Рис. 6-4 Изменение элементов живого сечения (χ; 𝜔; υ; Q) с изменением относительной ширины β трапецеидального канал Положим, что, исходя из этих данных, требуется запроектировать поперечный профиль канала (т.е. найти его размеры). Такая задача имеет много решений. Можно наметить целый ряд различных поперечных профилей канала, удовлетворяющих указанным условиям (см. рис. 6-4, а); для этого чертежа имеем
где индексами 1, 2 ... обозначены величины, относящиеся соответственно к 1, 2, 3-му, ... вариантам канала. На рисунке для примера показаны только три варианта; однако, рассматривая этот чертеж, надо себе представить множество таких вариантов, из которых первый характеризуется весьма малой глубиной, а последний — весьма малой шириной. Необходимая пропускная способность для первого варианта обеспечивается приданием каналу весьма большой ширины, а для последнего варианта — приданием каналу весьма большой глубины. Для рассматриваемых вариантов будем иметь:
Легко видеть, что первый и последний варианты будут характеризоваться относительно большой поверхностью трения, определяемой размером χ , равным b (для первого варианта) и 2h (для последнего варианта); поэтому скорость v для этих крайних вариантов должна быть относительно малой. Из сказанного вытекает, что среди ряда рассматриваемых вариантов имеется такой промежуточный, для которого средняя скорость υ оказывается максимальной
а следовательно, площадь живого сечения 𝜔 (равная Q0: υ )— минимальной:
Поперечный профиль, удовлетворяющий этим условиям, и является гидравлически наивыгоднейшим. Как видно, гидравлически наивыгоднейшим профилем трапецеидального канала называется профиль, который (при заданных т, i, п, Q) характеризуется максимально возможной средней скоростью v, а следовательно, минимальной площадью живого сечения. Обозначим относительную ширину по дну гидравлически наивыгоднейшего профиля через βг.н:
При этом все сказанное представим кривыми χ=f1 (β); 𝜔=f2 (β) и υ=f3 (β),показанными на рис. 6-4,б сплошными линиями (расположенными выше оси β). Дополнительно ниже оси р на данном графике изобразим штриховыми линиями кривые χ=f4 (β); 𝑄=f5 (β) и υ=f6 (β), построенные в предположении, что для проектирования вариантов, показанных на рис. 6-4,а, нам задано не Q=const, а 𝜔= const; расход Q с изменением β (при заданных 𝜔, т и i) — меняется. Из рассмотрения штриховых кривых видно, что гидравлически наивыгоднейшим профилем трапецеидального канала может быть назван также профиль, который (при заданных т, I ,п, 𝜔) характеризуется максимально возможной пропускной способностью. . Вертикаль I-II на рис. 6-4,6 отвечает максимумам и минимумам соответствующих функций, а следовательно, и величине βг.н. Рассматривая сплошные кривые графика, расположенные выше оси β, для определения величины βг.н , можем написать следующую систему двух уравнений
как видно, для отыскания βгн мы здесь приравняли нулю соответствующие производные (поскольку βгн отвечает минимуму функций 𝜔 и χ ). Подставляя в (6-31) выражения (6-18) и (6-19) и выполняя дифференцирование, получаем:
Решая эту систему уравнений, находим
Выражение (6-34) можно было бы найти и из рассмотрения кривойχ=f4 (β), показанной на графике штриховой линией ниже оси β. При этом пришлось бы только решать совместно уравнение (6-33) и уравнение
Выше мы искали гидравлически наивыгоднейшие размеры заданной формы (трапецеидальной). Можно, разумеется, поставить здесь и иную задачу: среди всех возможных форм поперечного сечения русла искать гидравлически наивыгоднейшую форму. Легко показать, что гидравлически наивыгоднейшей формой живого сечения является полукруг (поскольку в этом случае мы имеем минимальную величину χ, а следовательно, минимальную поверхность трения).
Рис. 6-5. Несовпадение минимальной площади живого сечения потока с минимальной площадью поперечного сечения земляной выемки
Стремясь получить минимальную стоимость каналов, откапываемых в грунте, их иногда проектируют, соблюдая условие β=βг.н , так при этом условии площадь живого сечения оказывается минимальной. Надо, однако, подчеркнуть, что в практике достаточно часто и отступают от указанного условия, причем проектируют каналы, принимая иные значения β (β Дополнительно необходимо учитывать следующее важное обстоятельство. Гидравлически наивыгоднейшие каналы получаются относительно глубокими; величина βдля них оказывается сравнительно малой. Такие глубокие каналы часто затруднительно откапывать в грунте и эксплуатировать. Вместе с тем можно показать, что кривая𝜔=f2(β) схематично представленная на рис. 6-4,б, является весьма пологой (ее минимум, выражен весьма слабо); достаточно принять для проектируемого канала площадь.живого учения равной не 𝜔мин, а, например, 1,03𝜔мин (т. е. увеличить 𝜔мин всего на 3 %), и мы при этом величину β получим относительно большой. В связи со сказанным, можно ввести понятие практически наивыгоднейшей величины βг.н(обозначим ее через β0г.н), при которой величина 𝜔 будет отличаться от 𝜔мин менее, чем на 3 — 4%, причем каналы будут получаться сравнительно малой г л у б и н ы. Величина β0г.н может иметь любое значение, лежащее в пределах:
где β0г.н- такая величина β,при которой 𝜔 отличается от 𝜔мин на 3—4%; значение (βг.н)предможно найти по формуле (предложенной нами):

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
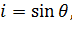 (6-1')
(6-1') см. на рисунке). Такое движение воды получается в искусственных цилиндрических каналах.
см. на рисунке). Такое движение воды получается в искусственных цилиндрических каналах.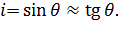 (6-1'')
(6-1'')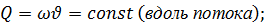 (6-2)
(6-2)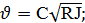 (6-3)
(6-3)
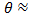 tg
tg  )
) i (6-4)
i (6-4)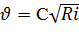 (6-5)
(6-5)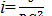 (6-6)
(6-6) (6-7)
(6-7)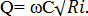 (6-8)
(6-8)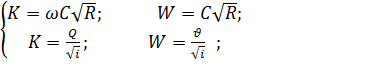 (6-9)
(6-9) (6-10)
(6-10)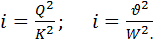 (6-11)
(6-11) (6-12)
(6-12)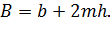 (6-13)
(6-13)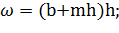 (6-14)
(6-14) (6-15)
(6-15)
 (6-16)
(6-16) (6-17)
(6-17) (6-18)
(6-18) (6-19)
(6-19)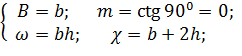 (6-20)
(6-20) (6-21)
(6-21)
 (6-22)
(6-22)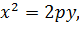 (6-23)
(6-23)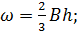 (6-24)
(6-24) (6-25)
(6-25)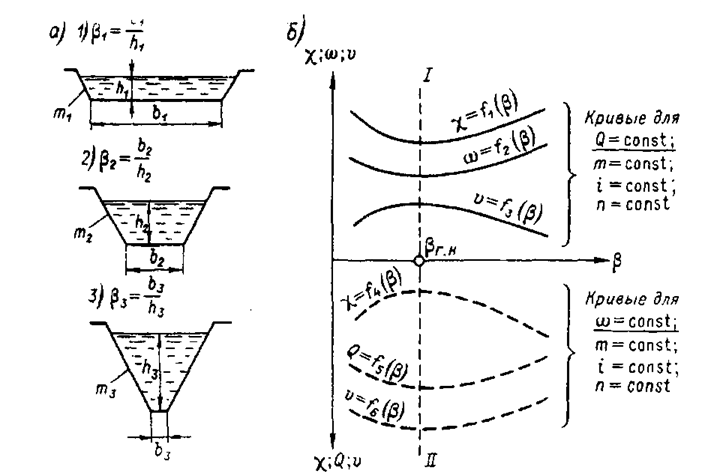
 (6-26)
(6-26) (6-27)
(6-27) (6-28)
(6-28)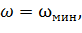 (6-29)
(6-29)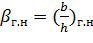 . (6-30)
. (6-30)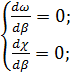 (6-31)
(6-31)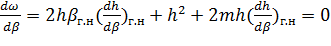 (6-32)
(6-32)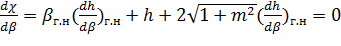 (6-33)
(6-33)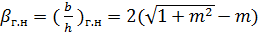 (6-34)
(6-34)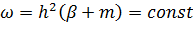
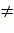 βг.н). Такое положение объясняется тем, что гидрав -лически наивыгоднейшие профили далеко не всегда оказываются экономически наивыгоднейшими. Действительно, экономически наивыгоднейший профиль канала должен характеризоваться минимумом объема земляных работ, а следовательно, для канала, выполняемого в выемке, минимальным значением площади выемки Ω = 𝜔 + 𝜔', а не площади живого сечения со (рис. 6-5).
βг.н). Такое положение объясняется тем, что гидрав -лически наивыгоднейшие профили далеко не всегда оказываются экономически наивыгоднейшими. Действительно, экономически наивыгоднейший профиль канала должен характеризоваться минимумом объема земляных работ, а следовательно, для канала, выполняемого в выемке, минимальным значением площади выемки Ω = 𝜔 + 𝜔', а не площади живого сечения со (рис. 6-5).