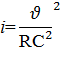ОСНОВНЫЕ ЗАДАЧИ ПРИ РАСЧЕТЕ ТРАПЕЦЕИДАЛЬНЫХ КАНАЛОВНА РАВНОМЕРНОЕ ДВИЖЕНИЕ ВОДЫ

Трапецеидальный канал характеризуется следующими шестью величи­нами b, h, т (эти три величины целиком определяют размеры живого сечения канала), n, i, Q (или v = Q/𝜔). Некоторые из приведенных величин бывают за­даны* теми или другими условиями проектирования. Задача гидравлического расчета обычно состоит в том, чтобы зная пять из названных величин, найти шестую. Ниже излагаются установившиеся в практике шаблоны решения такого рода вопросов, связанных с расчетом и проектированием каналов (слово «задача» здесь применяется в несколько условном смысле).

1°. Задачи, в которых живое сечение канала задано, т. е. в число заданных величин входят b, hи m.Эти задачи решаются непосредственно, без подбора искомой величины.

Задача 1. Даны все размеры живого сечения (т. е. величины b, h, m), уклон дна i и коэффициент шероховатости п. Требуется найти шестую величину — расход Q воды в канале.

Ход решения задачи:

1) Зная размеры живого сечения, находим 𝜔 иχ [по зависимостям

(6-14) и (6-15)];

2) находим R =𝜔/х;

3) зная R и n, по данным § 4-13 находим С;

4) зная С и Я, определяем v:

5) зная v и 𝜔, находим Q:

Задача 2. Даны все размеры живого сечения (т. е. величины b, h, т), и и Q. Требуется найти шестую величину — неизвестную iт. е. уклон дна канала, при котором канал заданного поперечного сечения и шероховатости будет про­пускать заданный расход Q.

Ход решения задачи:

1) так же, как и выше, находим величины 𝜔, χ, R, С;

2) зная 𝜔, находим v:

3) по формуле (6-6)

Рис. 6-6. К задаче 3 Рис. 6-7. К задаче 4

вычисляем i .

2°. Задачи, в которых живое сечение канала не задано, т. е. в число искомых величин входит b или h. Задачи этой группы всегда решаются путем подбора искомой величины.

Задача 3. Даны m, b, n, i, Q. Требуется найти глубину наполнечад канала h.

Ход решения задачи:

1) находим модуль расхода, которым должен характеризоваться рассчи-
тываемый канал. Этот модуль будем называть необходимым и

обозначать через К_необх : очевидно,

2) составляем таблицу по форме 1, в которой задаемся рядом значений h, и для каждого h вычисляем соответствующий модуль расхода К;

3) по данным 1-й и 10-й строк таблицы строим на рис. 6-6 график K=f(h)

4) по этому графику, зная K_необх, находим искомое h, как показано на
чертеже (см. h_иск).

Заметим, что кривая К = f(h) имеет выпуклость, обращенную в сторону оси h, и проходит через начало координат (так как при h = 0 значение К=0).

Задача 4. Даны т, h, n, i, Q. Требуется подобрать необходимую ширину канала по дну b.

Ход решения задачи:

1) находим необходимый модуль расхода:

Форма1

№ строки	Величина или расчетная формула	Единица измерения	Задаваемые и находимые численные значения	Примечания
	h	м	h1	h2	h3	…
	mh	м	…	…	…	…	m=…
	b+mh	м	…	…	…	…	b=
	𝜔=(b+mh)h	м2	…	…	…	…
		м	…	…	…	…
		м	…	…	…	…
		м	…	…	…	…
	C		…	…	…	…	по формуле….. при n=
			…	…	…	…
			…	…	…	…

Примечания. 1) При построении такого рода плавных кривых желательно (с целью экономии времени) вычислять возможно меньшее число точек; вместе с тем намечать менее четырех точек нельзя (четвертая точка должна рассматриваться как контрольная); в данном частном случае четвертой точкой может являться начало координат. Подчеркнем, что всякого рода вычисле­ния, подобные поясненным выше, всегда должны выполняться в виде таблиц (а не в «строчку»). Форма таких таблиц должна быть предварительно разработана с таким расчетом, чтобы в них помещались результаты всех арифметических вычислений.

2) Необходимо иметь в виду, что расчеты, осуществляемые методом подбора и выполняемые, например, в табличной форме, как то пояснено выше, не включаются в пояснительные записки к проектам сооружений. Такого рода расчеты остаются в черновиках. В пояснительной же записке указывается только окончательно найденное значение и дается поверочный расчет.

№ строки	Величина или расчетная формула	Единица измерения	Задаваемые и находимые численные значения	Примечания
	b	м	b1	b2	b3	…
	b+mh	м	…	…	…	…	m=…; mh=
	𝜔=(b+mh)h	м2	…	…	…	…	h=
		м	…	…	…	…
		м	…	…	…	…
	C		…	…	…	…	по формуле….. при n=
			…	…	…	…
			…	…	…	…

2) составляем таблицу по форме 2, в которой задаемся рядом значений b и для каждого b вычисляем соответствующий модуль расхода К;

3) по данным 1-й и 8-й строк таблицы строим график (рис. 6-7) К =f(b);

4) по этому графику, зная К_необх,находим искомое b.

Заметим, что кривая К = f(b) не проходит через начало координат. Модуль расхода К' указанный на графике, отвечает треугольному руслу (когда b=0) .

Задача 5. Даны m, n, i, Q, β. Требуется найти b и h.

Ход решения задачи:

1) находим необходимый модуль расхода:

2) составляем таблицу по форме 1, дополняя ее одной строкой: b = βh.
В этой таблице задаемся рядом значений h (в строке 1) и затем в дополнительной строке 2 вычисляем соответствующие значения b; после этого вычисляем
соответствующие значения К;

3) строим график (рис. 6-6)

4) по этому графику находим искомую глубину h_иск;

5) зная h, определяем b (b=βh).

3°. Задачи, в которых среди заданных величин — средняя скорость υ. Рас­смотрим следующие задачи.

Задача 6. Даны m, b, h (т.е. задано живое сечение), п, υ. Требуется найти Q и i.

Ход решения задачи:

1) вычисляем площадь живого сечения 𝜔:

𝜔=(b+mh)h;

2) находим расход Q:

3) определяем уклон дна i :

где С и R легко могут быть найдены предварительно (см., например, задачу 1).

Задача 7. Даны: а) m, n, Q, υ; б) одна из величин: h или b. Требуется найти: а) уклон i; б) величину b или h.

Ход решения задачи:

1) вычисляем площадь живого сечения 𝜔:

2) имеем известное геометрическое уравнение

𝜔=(b+mh)h;

это уравнение содержит одно неизвестное: b или h. Решая данное уравнение, находим недостающий размер живого сечения;

3) уклон i определяем по формуле:

Задача 8. Даны т, n, Q, i , υ. Требуется найти b и h. Ход решения задачи:

1) вычисляем величину 𝜔 и модуль скорости W:

2) выписываем систему двух уравнений с двумя неизвестными

(I) 𝜔=(b+mh) h = f₁(b, h);

(II)

Эта система двух уравнений может быть переписана в виде

(I')

(II')

где А и В — известные числа;

3) искомые величины находим, решая указанную систему уравнений с не­известными b и h (путем подбора или графически).

Не нашли, что искали? Воспользуйтесь поиском по сайту: