Лабораторная работа №9. Двухмерный массив. Матрица.

Цель работы: овладение навыками работы с двухмерными массивами.

Задания

Условие вида «дана матрица размера M × N» означает, что вначале дается фактический размер двумерного массива-матрицы (количество строк M и количество столбцов N), а затем приводятся элементы этого массива (количество элементов равно M∙N). Если в задании явно не указывается, какие значения могут принимать размеры исходной матрицы, то предполагается, что и число строк, и число столбцов может изменяться в пределах от 2 до 10. Ввод и вывод элементов матрицы осуществляются по строкам.

Квадратной матрицей порядка M называется двумерный массив-матрица размера M × M.

Если в задании, связанном с созданием или преобразованием матрицы, не описан результирующий набор данных, то предполагается, что этим набором является созданная (преобразованная) матрица, и необходимо вывести все ее элементы.

1. Даны целые положительные числа M,N и набор из M чисел. Сформировать матрицу размера M × N, у которой в каждом столбце содержатся все числа из исходного набора (в том же порядке).

2. Дана матрица размера M × N. Вывести ее элементы в следующем порядке: первый столбец сверху вниз, второй столбец снизу вверх, третий столбец сверху вниз, четвертый столбец снизу вверх и т. д.

3. Дана матрица размера M × N и целое число K (1 ≤ K ≤ N). Найти сумму и произведение элементов K-го столбца данной матрицы.

4. Дана матрица размера M × N. В каждой строке матрицы найти минимальный элемент.

5. Дана матрица размера M × N. В каждом столбце матрицы найти максимальный элемент.

6. Дана матрица размера M × N. Найти номер ее строки с наибольшей суммой элементов и вывести данный номер, а также значение наибольшей суммы.

7. Дана матрица размера M × N. Найти номер ее столбца с наименьшим произведением элементов и вывести данный номер, а также значение наименьшего произведения.

8. Дана матрица размера M × N. Найти минимальный среди максимальных элементов ее столбцов.

9. Дана матрица размера M × N. В каждой ее строке найти количество элементов, меньших среднего арифметического всех элементов этой строки.

10. Дана матрица размера M × N. Найти номера строки и столбца для элемента матрицы, наиболее близкого к среднему значению всех ее элементов.

11. Дана целочисленная матрица размера M × N. Найти номер последнего из ее столбцов, содержащих равное количество положительных и отрицательных элементов (нулевые элементы матрицы не учитываются). Если таких столбцов нет, то вывести 0.

12. Дана целочисленная матрица размера M × N. Найти номер первого из ее столбцов, содержащих только нечетные числа. Если таких столбцов нет, то вывести 0.

13. Дана целочисленная матрица размера M × N, элементы которой могут принимать значения от 0 до 100. Различные столбцы матрицы назовем похожими, если совпадают множества чисел, встречающихся в этих столбцах. Найти количество столбцов, похожих на последний столбец данной матрицы.

14. Дана целочисленная матрица размера M × N. Найти количество ее столбцов, все элементы которых различны.

15. Дана целочисленная матрица размера M × N. Найти номер первого из ее столбцов, содержащих максимальное количество одинаковых элементов.

16. Дана матрица размера M × N. Найти количество ее столбцов, элементы которых упорядочены по убыванию.

17. Дана матрица размера M × N. Найти максимальный среди элементов тех столбцов, которые упорядочены либо по возрастанию, либо по убыванию. Если упорядоченные столбцы в матрице отсутствуют, то вывести 0.

18. Дана целочисленная матрица размера M × N. Найти элемент, являющийся максимальным в своей строке и минимальным в своем столбце. Если такой элемент отсутствует, то вывести 0.

19. Дана матрица размера M × N. Преобразовать матрицу, поменяв местами минимальный и максимальный элемент в каждой строке.

20. Дана матрица размера M × N. Преобразовать матрицу, поменяв местами минимальный и максимальный элемент в каждом столбце.

21. Дана матрица размера M × N. Поменять местами строки, содержащие минимальный и максимальный элементы матрицы.

22. Дана матрица размера M × N. Поменять местами столбцы, содержащие минимальный и максимальный элементы матрицы.

23. Дана матрица размера M × N. Поменять местами столбец с номером 1 и последний из столбцов, содержащих только положительные элементы. Если требуемых столбцов нет, то вывести матрицу без изменений.

24. Дана матрица размера M × N. Поменять местами столбец с номером N и первый из столбцов, содержащих только отрицательные элементы. Если требуемых столбцов нет, то вывести матрицу без изменений.

25. Дана матрица размера M × N (M и N — четные числа). Поменять местами левую верхнюю и правую нижнюю четверти матрицы.

26. Дана матрица размера M × N. Удалить строку, содержащую минимальный элемент матрицы.

27. Дана матрица размера M × N. Удалить столбец, содержащий максимальный элемент матрицы.

28. Дана матрица размера M × N. Удалить ее последний столбец, содержащий только отрицательные элементы. Если требуемых столбцов нет, то вывести матрицу без изменений.

29. Дана матрица размера M × N, содержащая как положительные, так и отрицательные элементы. Удалить все ее столбцы, содержащие только положительные элементы. Если требуемых столбцов нет, то вывести матрицу без изменений.

30. Дана квадратная матрица A порядка M. Найти сумму элементов ее главной диагонали, то есть диагонали, содержащей следующие элементы:

A_1,1, A_2,2, A_3,3, … , A_M,M.

31. Дана квадратная матрица A порядка M. Найти сумму элементов каждой ее диагонали, параллельной главной (начиная с одноэлементной диагонали А_1,M).

32. Дана квадратная матрица A порядка M. Найти среднее арифметическое элементов каждой ее диагонали, параллельной побочной (начиная с одноэлементной диагонали A_1,1).

33. Дана квадратная матрица A порядка M. Найти минимальный элемент для каждой ее диагонали, параллельной главной (начиная с одноэлементной диагонали А_1,M).

34. Дана квадратная матрица A порядка M. Найти максимальный элемент для каждой ее диагонали, параллельной побочной (начиная с одноэлементной диагонали A_1,1).

35. Дана квадратная матрица A порядка M. Зеркально отразить ее элементы относительно главной диагонали (при этом элементы главной диагонали останутся на прежнем месте, элемент А_1,2 поменяется местами с А_2,1, элемент А_1,3 — с A_3,1 и т.д.). Вспомогательную матрицу не использовать.

36. Дана квадратная матрица A порядка M. Зеркально отразить ее элементы относительно побочной диагонали. (при этом элементы побочной диагонали останутся на прежнем месте, элементA_1,1 поменяется местами с A_M,M, элемент А - с A_m−1,m и т.д.). Вспомогательную матрицу не использовать.

37. Дана квадратная матрица A порядка M. Повернуть ее на угол 180◦ (при этом элемент A_1,1 поменяется местами с A_M,M, элемент А_1,2 — с A_M,M−1 и т. д.). Вспомогательную матрицу не использовать.

Выполнение лабораторной работы

Для выполнения работы необходимо:

- формализовать задачу;

- разработать алгоритм решения задачи;

- составить блок-схему алгоритма;

- выбрать и обосновать представление входных, промежуточных и выходных данных;

- произвести кодирование;

- разработать набор тестов, на которых будет проверяться программа;

- продемонстрировать работу программы на наборе тестов;

- оформить работу и отчитаться по ней.

Методические указания к выполнению лабораторной работы

Задание

Дана квадратная матрица A порядка M. Повернуть ее на угол 90° в отрицательном направлении, то есть по часовой стрелке (при этом элемент A_1,1 перейдет в А_1,M, элемент А_1,M — в A_M,M и т. д.). Вспомогательную матрицу не использовать.

Выполнение

Работа с матрицей аналогична работе с массивом, перебор её элементов производится в цикле. Перебор элементов матрицы осуществляется в двух массивах, в одном перебираются строки, в другом столбцы.

Этап 1. Формализация. При повороте матрицы на 90° строки становятся столбцами. Т.е. элемент A_1,1 становится A_1,M, A_1,2 – A_2,M, A_1,3 – A_3,M , и т.д., элемент A_2,1 становится A_1,M-1, A_2,2 – A_2,M-1, A_2,3 – A_3,M-1 , и т.д., элемент A_3,1 становится A_1,M-2, A_3,2 – A_2,M-2, A_3,3 – A_3,M-2 , и т.д., …, элемент A_M-1,1 становится A_1,2, A_M-1,2 – A_2,2, A_M-1,3 – A_3,2 , и т.д., элемент A_M,1 становится A_1,1, A_M,2 – A_2,1, A_M,3 – A_3,1 , и т.д.

Элемент A_i,j становится A_j,M-(i-1).

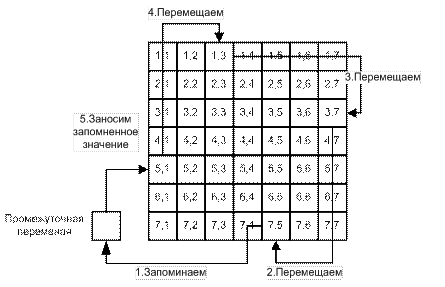
Таким образом, перемещая элементы согласно выведенной зависимости, можно повернуть матрицу на 90°. Однако заметим, что если просто перемещать элементы, получим неправильное решение, поскольку перемещаемые элементы замещают ещё неперемещённые элементы.

Решить эту проблему можно, выполняя перемещения так, как показано на рисунках:

Рис. 1. Первое перемещение

Рис. 2. Второе перемещение

Рис. 3. Третье перемещение

Рис. 4. Четвёртое перемещение

Рис. 5. Пятое перемещение

Рис. 6. Шестое перемещение

Выполнив перемещения внешних строк и столбцов, переходим к внутренним.

Рис. 7. Первое перемещение внутренней матрицы

Делаем перемещения до тех пор, пока не переместим элементы самой внутренней матрицы или пока не дойдём до матрицы, состоящей из одного элемента. В этом случае значение i будет меняться от M до (M div 2)+(M div 2)+1 (рис. 8).

Рис. 8. Изменение i

j будет зависеть от i и меняться от M-(i-1) до i-1 (рис. 9).

Рис. 9. Изменение j

Во всех перемещениях изменения индексов производится по одной и той же зависимости: jследующее=i, iследующее=M-(i-1). Всего перемещений будет три. Следовательно, можно задать ещё один цикл, в котором выполнять перемещения согласно зависимости. После последнего перемещения этого цикла заносим в вычисленную ячейку значение из промежуточной переменной.

Этап 2. Декомпозиция. Производим декомпозицию задачи — выделяем действия. Определяем, что для решения задачи необходимо выполнить следующие действия:

1. Вводим размер матрицы M.

2. Выполняем ввод. В циклах от 1 до M и от 1 до M вводим значения и присваиваем их элементам матрицы.

3. Выполняем вывод исходной матрицы. В циклах от 1 до M и от 1 до M выводим значения элементов матрицы на экран.

4. Выполняем преобразование. В циклах по i и по j перемещаем элементы матрицы.

5. Выполняем вывод преобразованной матрицы. В циклах от 1 до M и от 1 до M выводим значения элементов матрицы на экран.

Этап 3. Алгоритмизация. Составляем алгоритм решения задачи. Используем для записи алгоритма форму блок-схемы.

Блок-схема алгоритма выглядит следующим образом:

Этап 4. Кодирование. Переводим разработанный алгоритм на язык программирования — составляем программу. Новым в задании является описание и использование матрицы.

Не нашли, что искали? Воспользуйтесь поиском по сайту: