
|
|
Лабораторная работа №7. Оператор цикла с предусловиемЦель работы: изучение оператора цикла с предусловием.
Задания 1. Даны положительные числа A и B (A > B). На отрезке длины A размещено максимально возможное количество отрезков длины B (без наложений). Не используя операции умножения и деления, найти длину незанятой части отрезка A. 2. Даны положительные числа A и B (A > B). На отрезке длины A размещено максимально возможное количество отрезков длины B (без наложений). Не используя операции умножения и деления, найти количество отрезков B, размещенных на отрезке A. 3. Даны целые положительные числа N и K. Используя только операции сложения и вычитания, найти частное от деления нацело N на K, а также остаток от этого деления. 4. Дано целое число N >0. Если оно является степенью числа 3, то вывести TRUE, если не является — вывести FALSE. 5. Дано целое число N >0, являющееся некоторой степенью числа 2: N = 2K. Найти целое число K — показатель этой степени. 6. Дано целое число N >0. Найти двойной факториал N: N!! =N∙(N-2) ∙(N-4):.. (последний сомножитель равен 2, если N — четное, и 1, если N — нечетное). Чтобы избежать целочисленного переполнения, вычислять это произведение с помощью вещественной переменной и вывести его как вещественное число. 7. Дано целое число N >0. Найти наименьшее целое положительное число K, квадрат которого превосходит N: K2 > N. Функцию извлечения квадратного корня не использовать. 8. Дано целое число N >0. Найти наибольшее целое число K, квадрат которого не превосходит N: K2 ≤ N. Функцию извлечения квадратного корня не использовать. 9. Дано целое число N > 1. Найти наименьшее целое число K, при котором выполняется неравенство 3K > N. 10. Дано целое число N > 1. Найти наибольшее целое число K, при котором выполняется неравенство 3K < N. 11. Дано целое число N > 1. Вывести наименьшее из целых чисел K, для которых сумма 1 + 2 + ... + K будет больше или равна N, и саму эту сумму. 12. Дано целое число N > 1. Вывести наибольшее из целых чисел K, для которых сумма 1 + 2 + ... + K будет меньше или равна N, и саму эту сумму. 13. Дано число A > 1. Вывести наименьшее из целых чисел K, для которых сумма 1 + 1/2 + ... + 1/ K будет больше A, и саму эту сумму. 14. Начальный вклад в банке равен 1000 руб. Через каждый месяц размер вклада увеличивается на P процентов от имеющейся суммы (P — вещественное число, 0<P<25). По данному P определить, через сколько месяцев размер вклада превысит 1100 руб., и вывести найденное количество месяцев K (целое число) и итоговый размер вклада S (вещественное число). 15. Спортсмен-лыжник начал тренировки, пробежав в первый день 10 км. Каждый следующий день он увеличивал длину пробега на P процентов от пробега предыдущего дня (P — вещественное, 0<P<50). По данному P определить, после какого дня суммарный пробег лыжника за все дни превысит 200 км, и вывести найденное количество дней K (целое) и суммарный пробег S (вещественное число). 16. Дано целое число N >0. Используя операции деления нацело и взятия остатка от деления, вывести все его цифры, начиная с самой правой (разряда единиц). 17. Дано целое число N >0. Используя операции деления нацело и взятия остатка от деления, найти количество и сумму его цифр. 18. Дано целое число N > 0. Используя операции деления нацело и взятия остатка от деления, найти число, полученное при прочтении числа N справа налево. 19. Дано целое число N >0. С помощью операций деления нацело и взятия остатка от деления определить, имеется ли в записи числа N цифра «2». Если имеется, то вывести TRUE, если нет — вывести FALSE. 20. Дано целое число N >0. С помощью операций деления нацело и взятия остатка от деления определить, имеются ли в записи числа N нечетные цифры. Если имеются, то вывести TRUE, если нет — вывести FALSE. 21. Дано целое число N > 1. Если оно является простым, то есть не имеет положительных делителей, кроме 1 и самого себя, то вывести TRUE,иначе вывести FALSE. 22. Даны целые положительные числа A и B. Найти их наибольший общий делитель (НОД), используя алгоритм Евклида: НОД(A, B) = НОД(B, A mod B), если В 23. Дано целое число N > 1. Последовательность чисел Фибоначчи Fk определяется следующим образом: F1 = 1, F2 = 1, FK = FK−2 + FK−1, K = 3,4,.... Проверить, является ли число N числом Фибоначчи. Если является, то вывести TRUE, если нет — вывести FALSE. 24. Дано целое число N > 1. Найти первое число Фибоначчи, большее N. (определение чисел Фибоначчи дано в задании 24). 25. Дано целое число N > 1, являющееся числом Фибоначчи: N = Fk (определение чисел Фибоначчи дано в задании 24). Найти целые числа FK−1 и FK+1 — предыдущее и последующее числа Фибоначчи. 26. Дано целое число N > 1, являющееся числом Фибоначчи: N = Fk (определение чисел Фибоначчи дано в задании 24). Найти целое число K — порядковый номер числа Фибоначчи N. 27. Дано вещественное число ε > 0. Последовательность вещественных чисел A K определяется следующим образом: A1=2, AK = 2+1/АК−1 , K = 2,3,.... Найти первый из номеров K, для которых выполняется условие |AK − AK−1| < ε, и вывести этот номер, а также числа AK−1 и AK. 28. Дано вещественное число ε > 0. Последовательность вещественных чисел A K определяется следующим образом: A1 = 1, A2 = 2, AK = (AK−2 + 2∙AK−1)/3, K = 3,4,.... Найти первый из номеров K, для которых выполняется условие |AK − AK−1| < ε, и вывести этот номер, а также числа AK−1 и AK. 29. Даны положительные числа A, B, C. На прямоугольнике размера A × B размещено максимально возможное количество квадратов со стороной C (без наложений). Найти количество квадратов, размещенных на прямоугольнике. Операции умножения и деления не использовать.

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
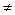 0; НОД(A, 0) = A.
0; НОД(A, 0) = A.