
|
|
Предел подпоследовательности сходящейся последовательности.Определение. Пусть x1,x2,…,xn,… (1) Некоторая числовая последовательность. Рассмотрим произвольную, возрастающую последовательность натуральных чисел {nk}: n1<n2<… Построим новую последовательность
Пример. xn=n : 1,2,3,.. Подпоследовательности: 2,4,6,8,… и 1,3,5,… Теорема 1. Если последовательность имеет предел, то любая ее подпоследовательность сходится и имеет тот же предел. Доказательство. Пусть xn→а, n→¥, возьмем e>0, ему отвечает номер N такой, что Пусть Найдем такой номер Теорема 2 (теорема Больцано-Вейерштрасса).Из каждой ограниченной числовой последовательности можно извлечь сходящуюся подпоследовательность. Доказательство. Пусть {xn}-ограниченная, тогда существуют конечные числа а0 и b0 такие, что "nÎN Þ а0£xn£b0, т.е. "nÎN xnÎ[а0;b0]. Разделим промежуток [а0;b0] пополам. Хотя бы в одной половине этого промежутка будет содержаться бесконечное множество элементов последовательности {xn} (т.к. иначе во всем промежутке [а0;b0] их было бы конечное число). Обозначим эту половину через [а1;b1]. (Если обе половины промежутка [а0;b0] содержат бесконечное множество элементов последовательности {xn}, то через [а1;b1] обозначим одну и только одну из них.) b1-а1= Промежуток [а1;b1] так же делим пополам и берем ту его половину, которая содержит бесконечное множество элементов последовательности {xn}. Обозначим эту половину через [а2;b2]. b2-а2= Продолжая этот процесс, получим две бесконечные последовательности: a0,a1,…,ak,…(a0£a1£…£ak£…) (1) b0,b1,…,bk,…(b0³b1³…³bk³…) (2) bk-аk= Последовательность (1) – неубывающая и ограниченная сверху, например числом b0; последовательность (2) невозрастающая и ограничена снизу, например числом а0. Значит обе эти последовательности имеют конечные пределы. Пусть
Т.о. последовательности (1) и (2) имеют один и тот же конечный предел с. Покажем, что из последовательности {xn} можно выделить подпоследовательность Из элементов последовательности {xn}, попавших в промежуток [а1;b1], возьмем какой-нибудь один, обозначим его Аналогичным образом можно найти ak£ Следовательно, по теореме о пределе промежуточной последовательности, Пусть {xn}-ограниченная т.е. 1) Рассмотрим случай, когда множество значений последовательности {xn} конечно: {a1,a2,…,ak}. В этом случае существует постоянная подпоследовательность 2) Множество значений последовательности {xn}бесконечно. М={Множество значений последовательности {xn}} – бесконечно и ограничено (т.к. {xn}-ограниченная). Согласно «лемме о предельной точке», множество М содержит хотя бы одну предельную точку – точку а. В окрестности точки а бесконечно много элементов множества М. Выберем из этой окрестности элемент Уменьшим окрестность так, чтобы в нее не попал элемент Выберем элемент Уменьшим окрестность так, чтобы в нее не попал элемент Выберем элемент Определение.Пусть дана последовательность {xn}. Предел ее подпоследовательности называется частичным пределом данной последовательности. Примеры.1) Последовательность xn=n не имеет частичных пределов. 2) последовательность 1,0,1,0,… имеет 2 частичных предела 1 и 0. Пусть дана последовательность {xn}. А={множество всех частичных пределов}. Рассмотрим случай, когда множество А ограничено и сверху, и снизу. Тогда существуют минимальный и максимальный элементы множества А: min A=a и max A=b. Определение. Наибольший из всех частичных пределов последовательности {xn} называется верхним пределом последовательности. Наименьший – нижним пределом. Обозначения: Теорема 4. Для любого числа e>0 $N=N(e): "n>N все элементы последовательности {xn} входят в интервал ( Доказательство. Т.к. Теорема 5.Для того, чтобы числовая последовательность имела предел, необходимо и достаточно, чтобы она была ограниченной и чтобы ее верхний и нижний пределы совпадали. Доказательство. Необходимость. Пусть последовательность {xn} сходится, тогда она ограничена и имеет единственный предел. Следовательно, Достаточность. Пусть 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 :
:  .
.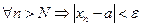 .(*)
.(*)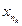 →а при k→¥.
→а при k→¥.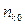 , что
, что  , т.е.
, т.е.  =а. ч.т.д.
=а. ч.т.д. и а0£а1<b1£b0.
и а0£а1<b1£b0. и а0£а1£a2<b2£b1£b0.
и а0£а1£a2<b2£b1£b0.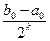 , k=1,2,…
, k=1,2,… =с. Имеем bk-аk=
=с. Имеем bk-аk= 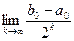 =0, то, переходя в равенстве bk=аk+
=0, то, переходя в равенстве bk=аk+  =
=  Т.к. элементами х1,х2,…,
Т.к. элементами х1,х2,…, 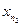 Î[а2;b2], причем n2>n1.
Î[а2;b2], причем n2>n1. Î[а3;b3] и n3>n2. Продолжая этот процесс, придем к последовательности
Î[а3;b3] и n3>n2. Продолжая этот процесс, придем к последовательности 
 , k=1,2,… и имеет предел.
, k=1,2,… и имеет предел. и чтобы длина окрестности была не больше
и чтобы длина окрестности была не больше  .
. ≠a из новой окрестности так, чтобы n3>n2. И так до бесконечности. В результате получим подпоследовательность
≠a из новой окрестности так, чтобы n3>n2. И так до бесконечности. В результате получим подпоследовательность 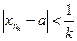 ч.т.д.
ч.т.д. =
=  - нижний предел,
- нижний предел,  =
=  - верхний предел.
- верхний предел.