
|
|
Счетные и несчетные множества.Свойства прообразов и образов
Обратная функция. Определение.Пусть функция f:A→B. 1) Если для любых двух различных элементов х1 и х2 из А их образы у1=f(x1) и у2=f(x2) также различны, х1≠х2 Отображение Формально это значит, что если два образа совпадают, то совпадают и прообразы ( (Инъекцию можно также определить как отображение, для которого существует левое обратное, т.е. Примеры 1. 2. 3.
2) Отображение Т.е. если f(X)=Y или В общем случае, т.е. когда f(X)ÌY, говорят, что f есть отображение X «в» Y.
Эквивалентные определения Следующие свойства отображения 1. F сюръективно 2. каждый элемент множества Y имеет хотя бы один прообраз во множестве X при отображении F. 3. образ множества X при отображении F(X) совпадает с Y 4. F имеет правое обратное отображение, т.е. такое отображение Примеры 1. 2. 3. Отображение f которое одновременно является инъекцией и сюръекцией, называетсябиекциейиливзаимно однозначнымсоответствием между А и В. В этом случае множества А и В находятся во взаимно однозначном соответствии.
Функция 1. Переводит разные элементы множества X в разные элементы множества Y (инъективность). Иными словами, o 2. Любой элемент из Y имеет свой прообраз (сюръективность). Иными словами, o Биекцию также называют взаимно однозначным отображением. (Множества, для которых существует биекция, называются равномощными.)
Примеры · ( · · f(x) = ex — биективная функция в · f(x) = sinx не является биективной функцией, если считать её определённой на всём · Функция · Если функции f и g биективны, то и композиция функций Можно определить новую функцию: f-1:B→A, x=f-1(y) – обратная функция, относительно f. Примеры. 1) f(x)=ex (график) f:(-∞;+∞)→(0;+∞) f-1: (0;+∞)→(-∞;+∞) ex=y 2) y=x2 (график) f:(-∞;+∞)→[0;+∞) Функция не является (не является инъекцией) взаимно однозначной. Рассмотрим только одну ветвь f: [0;+∞)→[0;+∞) x2=y Любая строго монотонная функция имеет обратную (т.к. является взаимно однозначной). Суперпозиция функций (сложная функция). Пусть есть 2 функции: ¦: A→B и g: D→F Пусть область определения D функции g входит в область значений функции f (DÌB). Тогда можно определить новую функцию – суперпозицию (композицию, сложную функцию) функций f и g: z=g(¦(x)). Примеры.f(x)=x2, g(x)=ex. f:R→R, g:R→R. ¦(g(x))=e2x, g(¦(x))= Определение Пусть
Свойства композиции · Композиция ассоциативна:
· Если F = idX — тождественное отображение на X, то есть
то
· Если G = idY — тождественное отображение на Y, то есть
то
· Рассмотрим пространство всех биекций множества X на себя и обозначим его · Группа Дополнительные свойства · Композиция непрерывных функций непрерывна. Пусть · Композиция дифференцируемых функций дифференцируема. Пусть
Счетные и несчетные множества. Два конечных множества состоят из равного числа элементов, если между этими множествами можно установить взаимно однозначное соответствие. Число элементов конечного множества – мощность множества. Для бесконечного множества можно установить взаимно однозначное соответствие между всем множеством и его частью. Самым простым из бесконечных множеств является множество N. Определение. Множества А и В называются эквивалентными(А~В), если между ними можно установить взаимно однозначное соответствие. Если эквивалентны два конечных множества, то они состоят из одного и того же числа элементов. Если же эквивалентные между собой множества А и В произвольны , то говорят, что А и В имеют одинаковуюмощность. (мощность = эквивалентность). Для конечных множеств понятие мощности совпадает с понятием числа элементов множества. Определение. Множество называется счетным, если можно установить взаимно однозначное соответствие между ним и множеством натуральных чисел. (Т.е. счетное множество – бесконечное, эквивалентное множеству N). (Т.е. все элементы счетного множества можно занумеровать). 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 ;
;  ;
;  ;
;  . Заметим отсутствие равенства в этом случае.
. Заметим отсутствие равенства в этом случае.  f(x1)≠f(x2) (f(x1)=f(x2)
f(x1)≠f(x2) (f(x1)=f(x2)  называется инъекцией (или вложением, или отображением в Y), если разные элементы множества X переводятся в разные элементы множества Y. Т.е. если х1¹х2Þf(x1)¹f(x2).
называется инъекцией (или вложением, или отображением в Y), если разные элементы множества X переводятся в разные элементы множества Y. Т.е. если х1¹х2Þf(x1)¹f(x2). ). Инъективность является необходимым условием биективности (достаточно вместе с сюръективностью).
). Инъективность является необходимым условием биективности (достаточно вместе с сюръективностью). такое, что
такое, что  .)
.) — инъективно.
— инъективно.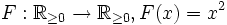 — инъективно.
— инъективно.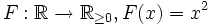 — не является инъективным (F( - 2) = F(2) = 4).
— не является инъективным (F( - 2) = F(2) = 4). .
.
 такое, что y=f(x), то отображение f действует на Y (отображение «на»).Такое отображение также называется сюръекцией.
такое, что y=f(x), то отображение f действует на Y (отображение «на»).Такое отображение также называется сюръекцией. .
. — сюръективно.
— сюръективно. — не является сюръективным.
— не является сюръективным.
 называется биекцией (и обозначается
называется биекцией (и обозначается  ), если она:
), если она: .
. .
. — функция, сохраняющая все элементы множества X, биективна на этом множестве.)
— функция, сохраняющая все элементы множества X, биективна на этом множестве.) — биективные функции из
— биективные функции из  в себя. Вообще, любой моном одной переменной нечетной степени является биекцией.
в себя. Вообще, любой моном одной переменной нечетной степени является биекцией. . Но если её рассматривать как функцию в
. Но если её рассматривать как функцию в  .
. такая, что
такая, что 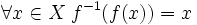 и
и 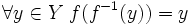 .
. биективна, в этом случае
биективна, в этом случае  . Коротко: композиция биекций является биекцией. Обратное, вообще говоря, неверно: если
. Коротко: композиция биекций является биекцией. Обратное, вообще говоря, неверно: если  f-1(x)=
f-1(x)= 
 .
. две функции. Тогда их композицией называется функция
две функции. Тогда их композицией называется функция  , определённая равенством:
, определённая равенством: .
. .
. ,
,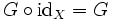 .
. ,
, .
. . То есть если
. То есть если  , то
, то  — биекция. Тогда композиция функций из
— биекция. Тогда композиция функций из  — группой. idX является нейтральным элементом этой группы. Обратным к элементу
— группой. idX является нейтральным элементом этой группы. Обратным к элементу 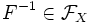 — обратная функция.
— обратная функция. .
. — топологические пространства. Пусть
— топологические пространства. Пусть  две функции,
две функции,  . Тогда
. Тогда  .
.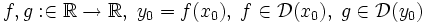 . Тогда
. Тогда 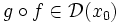 , и
, и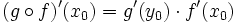 .
.