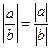|
|
Свойства отношения равномощности.1) А~А- рефлексивность. 2) А~В, то В~А – симметричность. 3) А~В и В~С, то А~С – транзитивность. Примеры. 1) n→2n, 2,4,6,… - четные натуральные 2) n→2n-1, 1,3,5,…- нечетные натуральные. Свойства счетных множеств. 1. Бесконечные подмножества счетного множества счетны. Доказательство. Т.к. А – счетно, то А: х1,х2,… - отобразили А в N. ВÌА, В: 2. Объединение конечной (счетной) системы счетных множеств – счетно. Примеры. 1. Множество целых чисел Z – счетно, т.к. множество Z можно представить как объединение счетных множеств А и В, где А: 0,1,2,.. и В: -1,-2,-3,… 2. Множество упорядоченных пар {(m,n): m,nÎZ} (т.е. (1,3)≠(3,1)). 3 (!). Множество рациональных чисел – счетно. Q=
Множество {(m,n)} – множество всех упорядоченных пар – счетно. Следовательно и множество {(p,q)} – счетно, а значит и Q – счетно. Определение. Иррациональным числом называется произвольная бесконечная десятичная непериодическая дробь, т.е. g0,g1g2… Множество всех десятичных дробей образуют множество вещественных (действительных) чисел. Множество иррациональных чисел – несчетно. Теорема 1. Множество вещественных чисел из промежутка (0,1) – несчетное множество. Доказательство. Допустим противное, т.е. что все числа интервала (0,1) можно занумеровать. Тогда, записывая эти числа в виде бесконечных десятичных дробей, получим последовательность: х1=0,а11а12…a1n… x2=0,a21a22…a2n… ………………….. xn=0,an1an2…ann… …………………… Рассмотрим теперь вещественное число х=0,b1b2…bn…, где b1- любая цифра, отличная от а11, (0 и 9), b2 - любая цифра, отличная от а22, (0 и 9),…, bn - любая цифра, отличная от ann, (0 и 9). Т.о. хÎ(0,1), но х¹xi (i=1,…,n) т.к. в противном случае, bi=aii. Пришли к противоречию. Ч.т.д. Теорема 2. Любой промежуток вещественной оси является несчетным множеством. Теорема 3.Множество действительных (вещественных) чисел – несчетно. Про всякое множество, равномощное множеству вещественных чисел говорят, что оно мощности континуума(лат. continuum – непрерывное, сплошное). Пример. Покажем, что интервал Функция у=tg x: Свойство полноты множества вещественных чисел. Теорема (свойство полноты множества вещественных чисел). Пусть А и В непустые подмножества множества вещественных чисел, обладающие следующим свойством:
Замечание. Множество рациональных чисел не обладает свойством полноты. Пример. Покажем, опираясь на эту теорему, что на множестве действительных чисел уравнение х2=2 имеет решение. Рассмотрим множества А={x>0: x2<2} и B={y>0: y2>2} Допустим, что х>yÞт.к. x,y>0, то x2>y2Þx2>2 – получили противоречие. Следовательно, по свойству полноты, $сÎR: "xÎA и "yÎB Þx£c£y. Покажем, что сÏА, т.е. условие с2<2 не выполняется. Допустим, что с2<2. Тогда взяв достаточно большое n с2+2с Тогда с+ Аналогично, через (с- Следовательно, с2=2. Плотность множества рациональных чисел в R. Теорема.Между любыми вещественными числами находится бесконечное множество рациональных чисел. (Т.е. множество Q всюду плотно в R). Доказательство. Возьмем числа a b (b>0) a<b, a,bÎR. Представим число b в виде бесконечной десятичной дроби:b=b0,b1b2… Построим приближения: b1=b0,b1, b2=b0,b1b2,…,bk=b0,b1b2…bk и т.д. Получим бесконечное множество рациональных чисел. Тогда, т.к. b>0, то все bk<b. Если из b вычесть bk, то b-bk=0, Следовательно, $k0: "k³k0 b-bk<b-aÞbk>a, т.е. a<bk<b "k³k0 Т.е. между числами а и b – множество рациональных чисел. Если b£0, то рассматриваются –b и –а. ч.т.д. Промежутки числовой прямой. Рассмотрим подмножества R.
a и b могут быть равны Модуль числа. Определение. Модулем числа а называется расстояние от начала вещественной оси (0) до точки, изображающей а.
Свойства модуля. 1) 2) 3) 4) a£½a½ 5) ½-a½=½a½ 6) ½a+b½£½a½+½b½ (½a1+a2+…+an½£½a1½+½a2½+…+½an½) 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 →1,
→1,  →2,… - поставили каждому элементу В в соответствие натуральное число, т.е. отобразили В в N. Следовательно В – счетно. Ч.т.д.
→2,… - поставили каждому элементу В в соответствие натуральное число, т.е. отобразили В в N. Следовательно В – счетно. Ч.т.д. . Можно установить взаимно однозначное соответствие между множеством несократимых дробей Q и множеством упорядоченных пар:
. Можно установить взаимно однозначное соответствие между множеством несократимых дробей Q и множеством упорядоченных пар: . Т.о. множество Q равномощно множеству {(p,q)}Ì{(m,n)}.
. Т.о. множество Q равномощно множеству {(p,q)}Ì{(m,n)}. обладает мощностью континуума.
обладает мощностью континуума. хÎА и
хÎА и  х£у, тогда существует такое действительное число с, что х£с£у.
х£у, тогда существует такое действительное число с, что х£с£у. с
с  R: х£с£у.
R: х£с£у. <2, т.е.
<2, т.е. +
+  <2Û2с
<2Û2с  bk+1bk+2 – эта разность будет сколь угодно мала.
bk+1bk+2 – эта разность будет сколь угодно мала.
 .
.